特殊な数列の計算として、数列の和や等差数列と等比数列の組み合わせがあります。問題の解き方を理解していない場合、これら数列の問題について、答えを得るのは難しいです。
数列の和を利用することにより、一般項を得ることができます。公式を覚える必要はないものの、\(n≧2\)である必要があるなど、ルールを理解しましょう。
なお等差数列と等比数列が組み合わさっている数列では、数列の和を利用することで等比数列を得られます。これにより、数列の和の計算が可能です。
数列を学ぶとき、これら特殊な数列の和と一般項を計算できるようになりましょう。そこで、どのように計算問題を解けばいいのか解説していきます。
数列の和を利用して一般項を得る
私たちが数列を学ぶとき、一般項を利用して数列の和を計算します。公式を利用することにより、数列の和を得ることができます。
一方、数列の和\(S_n\)がわかっている場合、数列の和を利用することによって一般項を計算できます。計算方法は簡単であり、以下のように一般項\(a_n\)を計算しましょう。
- \(S_n-S_{n-1}=a_n\)
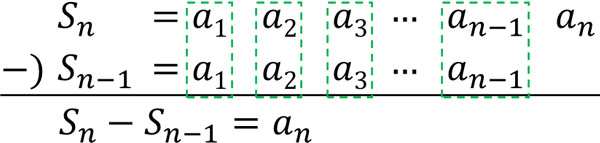
なお2つの数列の和を利用するため、\(n≧2\)である必要があります。\(n=1\)の場合、差を利用することができません。そのため数列の和を利用して一般項\(a_n\)を計算する場合、\(n=1\)のときも成り立つかどうか確認しましょう。
なお\(n=1\)が成り立たない場合、\(n=1\)のときと\(n≧2\)のときに分けて答えを記す必要があります。それでは、以下の問題の答えは何でしょうか。
- 初項から第\(n\)項までの和が\(S_n=2n^2-3n\)となる数列の一般項\(a_n\)を求めましょう。
以下のように計算しましょう。
\(a_n=S_n-S_{n-1}\)
\(a_n=2n^2-3n-2(n-1)^2\)\(+3(n-1)\)
\(a_n=2n^2-3n-2(n^2-2n+1)\)\(+3n-3\)
\(a_n=4n-5\)
なお\(n=1\)のとき、\(a_1=-1\)であり、さらには\(S_1=-1\)です。\(n=1\)のときも成り立つため、\(a_n=4n-5\)とわかります。
ちなみに、\(n=1\)のときに\(a_1=S_1\)となったのはたまたまであり、\(a_1=S_1\)とならないケースも多いです。この場合、前述の通り\(n=1\)のときと\(n≧2\)のときに分けて答えを記す必要があります。
シグマ記号と部分数列の計算方法
なお和の計算をするとき、数列のうち特定の項のみを計算したいときがあります。その場合、条件を変えることによって和の計算をしましょう。このとき、一般項を利用して項数を変化させます。
例えば項数が\(2n\)の場合、項数が偶数となる項のみを選ぶことができます。また項数が\(2n-1\)の場合、奇数の項のみを選ぶことができます。それでは、特定の項のみを選んで足す場合、どのように計算すればいいのでしょうか。
例えば一般項\(a_n=4n-5\)がある場合、以下の計算をしてみましょう。
- \(S_n=a_1+a_3+a_5+…+a_{2n-1}\)
項数は\(2n-1\)であるため、奇数の項のみを足すことになります。つまり、項数を\(n\)から\(2n-1\)へ変えることにより、奇数のみの一般項を表すことができます。そこで、以下のように計算しましょう。
\(a_{2n-1}=4(2n-1)-5\)
\(a_{2n-1}=8n-9\)
項が奇数となる場合の一般項を表したら、シグマと公式を利用して和の計算をしましょう。
\(S_n=\displaystyle\sum_{k=1}^{n}{(8k-9)}\)
\(S_n=8·\displaystyle\frac{1}{2}n(n+1)-9n\)
\(S_n=4n^2-5n\)
こうして、特定の項のみを足す場合の計算をすることができました。
等差数列と等比数列を組み合わせる和の計算
等差数列と等比数列を組み合わせた式についても、数列の和\(S\)を利用することによって問題を解くことができます。特殊な数列であるため、問題の解き方を知っていないと答えを得るのは難しいです。
以下は等差数列と等比数列を組み合わせた式です。
- \(S=1·1+2·3+3·3^2+…\)\(+n·3_{n-1}\)
数列の各項の左側は初項1、公差1の等差数列です。また数列の各項の右側は初項1、公比3の等比数列です。計算方法は決まっており、公比(今回の例では3)をかけます。その後、上の式から下の式を引きましょう。

次に、上図のオレンジ枠で囲った部分に着目しましょう。以下の部分になります。
\(1·3+1·3^2+…+1·3^{n-1}\)
確認すると初項3、公比3の等比数列の和であるとわかります。注意点は項数です。式を確認すると\(3^{n-1}\)となっており、第1項から第\(n-1\)項までの項が存在するとわかります。つまり、項数は\(n-1\)です。
そこで等比数列の和の公式を利用することにより、以下のように計算しましょう。
\(-2S=1·1+\displaystyle\frac{3(3^{n-1}-1)}{3-1}-n·3^n\)
\(-2S=1+\displaystyle\frac{3^n}{2}-\displaystyle\frac{3}{2}-n·3^n\)
\(-2S=\displaystyle\frac{3^n}{2}(1-2n)-\displaystyle\frac{1}{2}\)
\(S=\displaystyle\frac{3^n}{4}(2n-1)+\displaystyle\frac{1}{4}\)
こうして、数列の和を計算することができました。数列の和に対して公比をかけ、引き算をした後、一部の数列に着目することで答えを得ることができます。
数列の和を利用して計算問題を解く
特殊な数列では、解き方を理解していないと答えを得ることができません。こうした特殊な数列の中でも、数列の和を利用することによって計算しなければいけないケースがあります。
一般項を得たい場合、\(S_n-S_{n-1}=a_n\)によって計算しましょう。この場合は\(n=1\)を含まず、\(n≧2\)のときに成り立ちます。そこで、\(n=1\)についても成り立つかどうかを確認しなければいけません。
また等差数列と等比数列を組み合わせた式を計算することもあります。この場合は数列の和に対して公比をかけた後、引き算をしましょう。計算方法は特殊ですが、これによって数列の和の式を得ることができます。
数列の性質を利用することにより、特殊な数列の答えを計算できます。そこで、問題の解き方を学びましょう。






