複素数平面で重要な要素に回転があります。回転が関わる図形では、複素数平面を利用することによって容易に計算できます。
このとき、複素数を極形式で表しましょう。角度と長さを利用することにより、複素数平面で複素数を表現できるのです。またかけ算や割り算をすることにより、回転や拡大・縮小を計算できるようになります。
なお回転させるとき、原点以外の点を中心に回転させたいケースがあります。このときについても、計算できるようになりましょう。
それでは、どのように極形式を利用して複素数を表せばいいのでしょうか。また、どのようにかけ算や割り算を利用して点を回転させればいいのでしょうか。複素数平面で極形式を利用し、かけ算や割り算をする方法を解説していきます。
もくじ
角度を利用して表す複素数が極形式
複素数を複素数平面で表すとき、以下の二種類の方法があります。

私たちが慣れているのは\(A(a,b)\)などのように、座標を利用することで点を表す方法です。一方、座標を利用しなくても、長さ\(r\)と角度\(θ\)を利用することによって一つの点を表すこともできます。
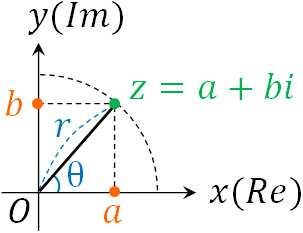
複素数の極形式では、原点Oから点Aまでの長さ\(r\)と角度\(θ\)を利用して点を表します。例えば複素数\(z=a+bi\)について、長さ\(r\)、角度\(θ\)のとき、以下の式によって点を表すことができます。
- \(z=r(cosθ+isinθ)\)

図より、\(z=a+bi\)について、\(a=rcosθ\)、\(b=rsinθ\)です。そのため、\(z=rcosθ+i·rsinθ\)であり、\(z=r(cosθ+isinθ)\)へと変形できます。このとき、角度\(θ\)を偏角といいます。
複素数を極形式で表す
それでは、複素数を極形式で表せるようになりましょう。以下の図を確認すると、\(cosθ=\displaystyle\frac{a}{r}\)、\(sinθ=\displaystyle\frac{b}{r}\)とわかります。
また、\(r=\sqrt{a^2+b^2}\)です。そこで長さ\(r\)を計算した後、角度を計算することによって複素数を極形式で表しましょう。以下の問題の答えは何でしょうか。
- \(z=2+2i\)を極形式で表しましょう。なお、偏角は\(0≦θ<2π\)です。
長さは\(r=\sqrt{2^2+2^2}\)\(=2\sqrt{2}\)です。長さ\(r\)を利用すると、\(cosθ=\displaystyle\frac{1}{\sqrt{2}}\)、\(sinθ=\displaystyle\frac{1}{\sqrt{2}}\)になるとわかります。つまり、\(θ=\displaystyle\frac{π}{4}\)です。
そのため、\(z=2+2i\)を極形式で表すと以下のようになります。
- \(z=2\sqrt{2}\left(cos\displaystyle\frac{π}{4}+isin\displaystyle\frac{π}{4}\right)\)
このように、複素数を極形式によって表せるようになりましょう。
複素数のかけ算と割り算
なお、極形式で重要なのはかけ算と割り算です。複素数平面は回転を含む計算で有利であり、計算方法が容易です。点を回転させるとき、利用されるのがかけ算や割り算です。例えば、以下の複素数があるとします。
- \(z_1=r_1(cosθ_1+isinθ_1)\)
- \(z_2=r_2(cosθ_2+isinθ_2)\)
複素数の掛け算をするとき、極形式では以下のようになります。
- \(z_1z_2\)\(=r_1r_2\{cos(θ_1+θ_2)+isin(θ_1+θ_2\}\)
つまり極形式を利用してかけ算をするとき、長さ\(r\)(絶対値)はかけ算となり、角度\(θ\)は足し算となります。一方で割り算では以下のようになります。
- \(\displaystyle\frac{z_1}{z_2}\)\(=\displaystyle\frac{r_1}{r_2}\{cos(θ_1-θ_2)+isin(θ_1-θ_2\}\)
割り算をするとき、長さ\(r\)(絶対値)は割り算となり、角度\(θ\)は引き算となります。極形式を利用してのかけ算や割り算では、この関係を覚えましょう。それでは、以下の問題を解きましょう。
- \(α=\sqrt{3}+i\)、\(β=3+3i\)のとき、\(αβ\)と\(\displaystyle\frac{α}{β}\)を極形式で表しましょう。なお、偏角は\(0≦θ<2π\)です。
それぞれの複素数を極形式で表すと以下のようになります。
- \(α=2\left(cos\displaystyle\frac{π}{6}+isin\displaystyle\frac{π}{6}\right)\)
- \(β=3\sqrt{2}\left(cos\displaystyle\frac{π}{4}+isin\displaystyle\frac{π}{4}\right)\)
そのため、以下のように計算できます。
\(αβ\)
\(=6\sqrt{2}\)\(\left\{cos\left(\displaystyle\frac{π}{6}+\displaystyle\frac{π}{4}\right)+isin\left(\displaystyle\frac{π}{6}+\displaystyle\frac{π}{4}\right)\right\}\)
\(=6\sqrt{2}\left(cos\displaystyle\frac{5π}{12}+isin\displaystyle\frac{5π}{12}\right)\)
\(\displaystyle\frac{α}{β}\)
\(=\displaystyle\frac{\sqrt{2}}{3}\)\(\left\{cos\left(\displaystyle\frac{π}{6}-\displaystyle\frac{π}{4}\right)+isin\left(\displaystyle\frac{π}{6}-\displaystyle\frac{π}{4}\right)\right\}\)
\(=\displaystyle\frac{\sqrt{2}}{3}\)\(\left\{cos\left(-\displaystyle\frac{π}{12}\right)+isin\left(-\displaystyle\frac{π}{12}\right)\right\}\)
\(=\displaystyle\frac{\sqrt{2}}{3}\left(cos\displaystyle\frac{23π}{12}+isin\displaystyle\frac{23π}{12}\right)\)
こうして、極形式を用いてかけ算と割り算をすることができました。
複素数平面での回転と拡大・縮小
複素数平面は点の回転を計算するときに便利であると解説しました。この理由として、かけ算や割り算をするとき、角度の足し算または引き算によって計算できるからです。
極形式を利用して計算するとき、計算方法を覚えるだけでは意味がありません。複素数平面でどのように点が動くのか理解しましょう。
先ほど、かけ算によって長さ\(r\)はかけ算になり、偏角\(θ\)は足し算になると解説しました。これはつまり、その分だけ長さ\(r\)が拡大し、原点を中心に回転したことを意味しています。先ほどの問題であれば、以下の複素数について\(αβ\)を計算しました。
- \(α=2\left(cos\displaystyle\frac{π}{6}+isin\displaystyle\frac{π}{6}\right)\)
- \(β=3\sqrt{2}\left(cos\displaystyle\frac{π}{4}+isin\displaystyle\frac{π}{4}\right)\)
\(α×β\)というのは、\(α\)に対して長さを\(3\sqrt{2}\)倍した後、角度を\(\displaystyle\frac{π}{4}\)加えることを意味しています。
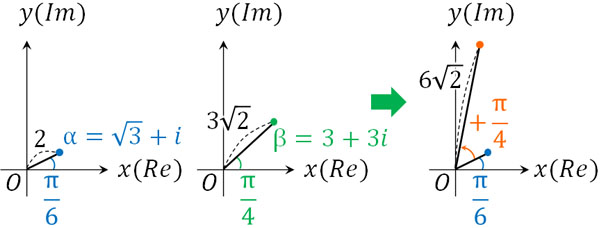
一方で割り算では、長さ\(r\)は縮小し、角度の引き算によって偏角が変化します。このように、極形式を利用したかけ算や割り算というのは、長さ\(r\)の拡大・縮小と点の回転に関与しているのです。
足し算、引き算の場合、複素数平面上を平行移動します。一方でかけ算と割り算では、点が回転する事実が重要です。点の移動と関連付けて極形式の計算を行うようにしましょう。それでは、以下の問題の答えは何でしょうか。
- \(z=2-6i\)について、原点を中心に\(\displaystyle\frac{π}{6}\)移動させた点を表す複素数を求めましょう。
原点を中心に\(\displaystyle\frac{π}{6}\)移動させるためには、長さ1、偏角\(\displaystyle\frac{π}{6}\)の複素数をかければいいとわかります。この条件を満たす複素数は以下になります。
\(cos\displaystyle\frac{π}{6}+isin\displaystyle\frac{π}{6}\)
\(=\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i\)
そのため\(\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i\)をかければ、原点を中心に\(\displaystyle\frac{π}{6}\)させた点を表すことができます。そこで、以下のように計算しましょう。
\((2-6i)\)\(\left(\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i\right)\)
\(=\sqrt{3}+i-3\sqrt{3}i-3i^2\)
\(=3+\sqrt{3}+(1-3\sqrt{3})i\)
こうして、複素数平面を利用して特定の角度を回転させるときの点を得ることができました。点を回転させたいとき、長さ1の複素数を利用してかけ算または割り算をしましょう。なお、回転に加えて長さの拡大・縮小をしたい場合、かけ算または割り算をするとき、複素数の長さ\(r\)を調節しましょう。
原点以外の点を中心に回転させる計算方法
先ほど、原点を中心に点を回転させる方法を解説しました。次に、原点以外の点を中心に回転させる方法を学びましょう。
点Aに対して、原点を中心に\(\displaystyle\frac{π}{6}\)回転させる場合、先ほど解説した通り\(\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i\)をかければいいです。それでは原点ではなく、点Bを中心にして点Aを\(\displaystyle\frac{π}{6}\)回転させるにはどうすればいいのでしょうか。
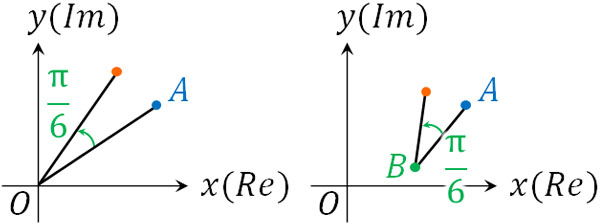
方法としては、平行移動を利用しましょう。足し算や引き算をすることにより、平行移動させることができることはすでに述べています。
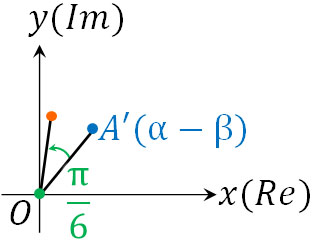
点A(複素数\(α\))について、点B(複素数\(β\))を中心に回転させる場合、線分BAを原点へ平行移動させましょう。\(α-β\)によって点Bの要素を引けば、点Aを移動させることで線分BAが原点へ移動します。

図の点A’(複素数\(α-β\))と原点をつなぐと新たな線分BA(線分OA’)になります。点Bを原点へ移動したため、複素数のかけ算(または割り算)によって回転させることができます。例えば原点を中心に\(\displaystyle\frac{π}{6}\)移動させたい場合、\(α-β\)に対して\(\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i\)をかけます。
ただ、最初に点Bの分だけ移動させているため、元の場所に戻さなければいけません。先ほど、点Bの要素を引くことで原点へ平行移動させました。\(-β\)を行うことで平行移動させているため、回転させた後は複素数\(β\)を加えることで、点Bを原点から元の場所へ戻しましょう。
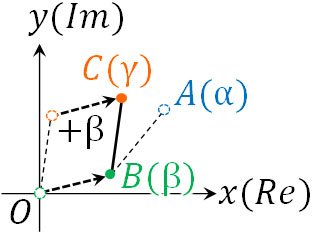
そのため点A(複素数\(α\))について、点B(複素数\(β\))を中心に\(θ\)だけ回転させることで得られる点C(複素数\(γ\))の式は以下になります。
- \(γ=(α-β)(cosθ-isinθ)+β\)
この式を覚えても意味がありません。問題文が変わると、公式を使えなくなるからです。そうではなく、なぜこの式によって点Bを中心に回転させることができるのか学びましょう。そうすれば、公式を覚えなくても式を得ることができます。
なお点を回転させた後、拡大または縮小させたい場合、原点へ移動させた後に\(k\)倍しましょう(\(k\)は実数)。\(k\)倍した後、点の場所を元に戻せば答えを得ることができます。
- \(γ=k(α-β)(cosθ-isinθ)+β\)
計算の原理を理解すれば、応用問題であっても対処できます。それでは、ここまで解説した内容を利用して計算問題を解きましょう。以下の問題の答えは何でしょうか。
- 点A(\(α=1+2i\))、点B(\(β=3+i\))、点C(\(γ=4+3i\))について、∠BACの大きさを求めましょう。
複素数平面の知識がなくても∠BACの大きさを計算することはできますが、ここでは先ほど解説した方法を用いて計算しましょう。\(∠BAC=θ\)として図を描くと以下のようになります。
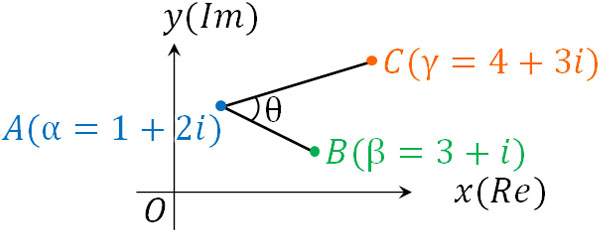
図を描くと、点Bについて、点Aを中心に回転&拡大させることで点Cと重なるとわかります。そこで点Bについて、点Aの分だけ平行移動させることで原点へ移動させましょう。その後、偏角θの分だけ回転させ、\(k\)倍し、さらには点Aの要素を加えて元の場所に戻せば点Cと重なります。
そのため、以下の式になります。
- \(γ=k(β-α)(cosθ+isinθ)+α\)
そこで、以下のように式を変形します。
\(γ-α=k(β-α)(cosθ+isinθ)\)
\(\displaystyle\frac{γ-α}{β-α}=k(cosθ+isinθ)\)
それぞれの点の位置はわかっているため、\(\displaystyle\frac{γ-α}{β-α}\)を計算しましょう。
\(\displaystyle\frac{γ-α}{β-α}=\displaystyle\frac{4+3i-(1+2i)}{3+i-(1+2i)}\)
\(=\displaystyle\frac{3+i}{2-i}\)
\(=\displaystyle\frac{(3+i)(2+i)}{(2-i)(2+i)}\)
\(=\displaystyle\frac{5+5i}{5}\)
\(=1+i\)
そのため、\(k(cosθ+isinθ)=1+i\)となります。角度を得る必要があるため、以下のように計算しましょう。
\(k(cosθ+isinθ)=1+i\)
\(k(cosθ+isinθ)=\sqrt{2}\left(\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{2}}i\right)\)
こうして\(k=\sqrt{2}\)、\(θ=\displaystyle\frac{π}{4}\)とわかりました。つまり、答えは\(∠BAC=\displaystyle\frac{π}{4}\)です。点Bについて、点Aを中心に\(\displaystyle\frac{π}{4}\)回転させ、長さを\(\sqrt{2}\)倍すると点Cに重なります。
複素数の極形式を利用して回転・拡大(縮小)させる
図形を利用するとき、複素数平面では点を回転させることができます。かけ算や割り算を利用することにより、長さが伸びたり縮んだりするだけでなく、原点を中心に点が回転するのです。
複素数を平面で表すとき、2つの方法があります。極形式はその一つであり、原点からの距離\(r\)と偏角\(θ\)を利用することにより、特定の点を表現できるのです。複素数平面で点を回転させるとき、極形式を利用しましょう。
なお原点を中心に点を回転させるのではなく、特定の点を中心に回転させたいケースがあります。この場合、点を平行移動させて回転や拡大(または縮小)させた後、点を元の位置に戻しましょう。これにより、原点以外の点を中心に回転させることができます。
複素数平面で点の回転が可能なのは優れており、回転が関わる計算では有利です。そこで複素数を極形式で表せるようになり、点の回転や拡大・縮小に関わる計算を行えるようになりましょう。






