放物線、楕円、双曲線：焦点や方程式、軌跡の計算、平行移動

私たちが学ぶ二次曲線で最も有名な式は\(y=ax^2\)です。\(y=ax^2\)は二次関数といわれますが、二次曲線でもあります。円も二次曲線の一種です。

こうした二次曲線には放物線や楕円、双曲線が含まれます。二次式になっている場合、図を描くと曲線になります。こうした曲線が二次曲線です。

二次曲線を学ぶとき、放物線や楕円、双曲線の方程式を学ばなければいけません。また、こうした二次曲線では焦点を利用します。方程式に焦点が含まれるのです。そこで、方程式を用いて軌跡の計算や平行移動を行えるようになりましょう。

それでは、どのように二次曲線の計算をすればいいのでしょうか。放物線、楕円、双曲線の方程式を解説していきます。

1 放物線の方程式と焦点の概念
- 1.1 円の中心の軌跡と放物線
2 楕円の方程式：円との関係
- 2.1 焦点が\(y\)軸上に存在する場合の式
- 2.2 円と楕円の関係：軌跡を利用して楕円を描く
3 双曲線の方程式の概要と決定
- 3.1 漸近線と双曲線の関係
4 二次曲線の平行移動と計算方法
5 放物線、楕円、双曲線の方程式を利用する

放物線の方程式と焦点の概念

まず、放物線はどのような曲線なのでしょうか。私たちが見慣れている二次関数に対して、横倒しにした曲線が放物線です。また\(y=ax^2\)によって二次関数を表せるのに対して、放物線では以下の式を利用します。

\(y^2=4px\)

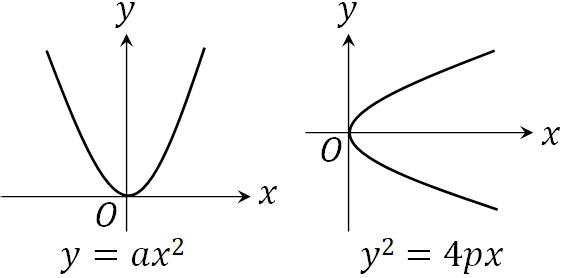
なぜ\(y^2=ax\)ではなく、\(y^2=4px\)という式なのでしょうか。放物線の式に存在する\(p\)は焦点です。そこで、放物線で利用される焦点が何を意味しているのか学びましょう。

まず、焦点として点F\((p,0)\)を置きましょう。\(p\)の値は何でもよく、ひとまず焦点を置きます。その後、\(y\)軸に対称な焦点に対してたて軸\((x=-p)\)を引きます。\((-p,0)\)を通るたて軸の線を準線といいます。

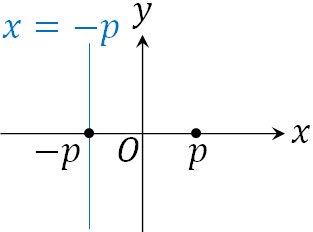
このとき、焦点\((p,0)\)と準線からの距離が等しい点A\((x,y)\)の軌跡を描きます。以下の図のように、\(AF=AH\)となるように点Aを描くと放物線になるのです。

つまり放物線というのは、焦点と準線からの距離が等しい点の軌跡を指します。なお、AHの長さは絶対値を利用して\(AH=|x-(-p)|\)\(=|x+p|\)と表すことができます。一方、AFは点と点の距離を計算することで表すことができます。

\(AF=\sqrt{(x-p)^2+(y-0)^2}\)

\(AF=\sqrt{(x-p)^2+y^2}\)

\(AH=AF\)であるため、以下のように計算しましょう。

\(|x+p|=\sqrt{(x-p)^2+y^2}\)

\(|x+p|^2=(\sqrt{(x-p)^2+y^2})^2\)

\((x+p)^2=(x-p)^2+y^2\)

\(y^2=4px\)

こうして、放物線の方程式を導出できました。公式を覚えるだけでなく、焦点の意味を理解しましょう。そうすれば、放物線が何を表している曲線なのかわかります。

なお放物線について、焦点Fが\((0,p)\)と\(y\)軸に存在する場合、\(y=ax^2\)のグラフになります。二次関数というのは、放物線の特殊なケースです。つまり私たちは特殊なケースをメインで学んでいたのです。

それでは、\(y^2=6x\)をグラフで描くとどのようになるでしょうか。\(y^2=4px\)であるため、\(4p=6\)を計算すると、\(p=\displaystyle\frac{3}{2}\)になります。つまり、\(\left(\displaystyle\frac{3}{2},0\right)\)が焦点です。

また\(y^2=6x\)に\(x=\displaystyle\frac{3}{2}\)を代入すると、\(y=±3\)となります。そこで、以下のようにグラフを描きましょう。

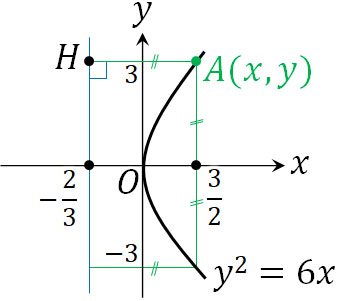
こうして、放物線を描くことができました。

円の中心の軌跡と放物線

それでは、円の中心の軌跡を利用して放物線を描きましょう。軌跡上の動点\((x,y)\)を利用して関係式を作り、放物線の方程式を得るのです。以下の問題の答えは何でしょうか。

円\((x-3)^2+y^2=4\)に外接し、\(x=-1\)に接する円の中心Aの軌跡を方程式で表しましょう。

2つの円が接するとき、外接と内接の二種類があります。今回は2つの円が外接する場合の軌跡であるため、以下の図を作りましょう。

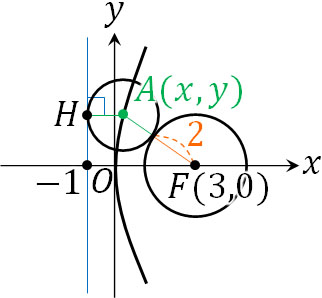
そこで、式を作ります。図を確認すると、2つの円の半径を足せばAFになるため、\(AF=AH+2\)とわかります。AHの長さは\(AH=x-(-1)\)\(=x+1\)です。また、AFの長さは以下のようになります。

\(AF=\sqrt{(x-3)^2+(y-0)^2}\)

\(AF=\sqrt{(x-3)^2+y^2}\)

そこで、以下の式を作りましょう。

\(AF=AH+2\)

\(\sqrt{(x-3)^2+y^2}=x+1+2\)

\(\sqrt{(x-3)^2+y^2}=x+3\)

\((x-3)^2+y^2=(x+3)^2\)

\(y^2=12x\)

こうして、円の中心の軌跡（放物線）を得ることができました。

楕円の方程式：円との関係

二次曲線では楕円も重要です。円を利用して計算問題を解いた経験は何度もあると思います。円は楕円の特殊なケースです。円では焦点を利用しませんが、2つの焦点が重なった状態が円というわけです。2つの焦点が重なることにより、円の中心となります。

それでは、楕円はどのような図形と定義されているのでしょうか。楕円というのは、2つの点（焦点）からの距離の和が等しい図形を指します。それでは、焦点がF\((c,0)\)、F’\((-c,0)\)である以下の楕円を考えてみましょう。

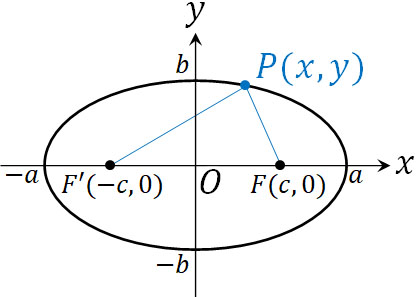
また上図のように、長軸（最も長くなる部分）の長さを\(2a\)、短軸（最も短くなる部分）の長さを\(2b\)とします。楕円の定義より、楕円上の点を\(P(x,y)\)とすると、以下の関係が成り立ちます。

\(FP+F’P=\)一定

なお、この式は以下のようになります。

\(FP+F’P=2a\)

なぜ「一定」の部分が\(2a\)かというと、下図のように、最も長い軸の距離\(2a\)が\(FP+F’P\)に該当するからです。

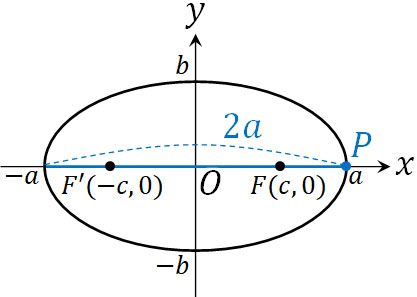
なお、2点間の距離を計算すると式は以下のようになります。

\(\sqrt{(x-c)^2+y^2}\)\(+\sqrt{(x+c)^2+y^2}\)\(=2a\)

そこで式を変形し、二乗を利用して以下のように計算しましょう。

\(\sqrt{(x-c)^2+y^2}\)\(+\sqrt{(x+c)^2+y^2}\)\(=2a\)

\(\sqrt{(x-c)^2+y^2}\)\(=2a-\sqrt{(x+c)^2+y^2}\)

\((x-c)^2+y^2\)\(=4a^2\)\(-4a\sqrt{(x+c)^2+y^2}\)\(+(x+c)^2+y^2\)

\(4a\sqrt{(x+c)^2+y^2}=4a^2+4cx\)

\(a\sqrt{(x+c)^2+y^2}=a^2+cx\)

そこで、再び両辺を二乗しましょう。

\(a\sqrt{(x+c)^2+y^2}=a^2+cx\)

\(a^2(x+c)^2+a^2y^2\)\(=a^4+2a^2cx+c^2x^2\)

\(a^2x^2-c^2x^2+a^2y^2\)\(=a^4-a^2c^2\)

\((a^2-c^2)x^2+a^2y^2\)\(=a^2(a^2-c^2)\)

重要なのは、\(a^2-c^2=b^2\)であることです。\(FP+F’P=2a\)であるため、以下の図を作ることができます。

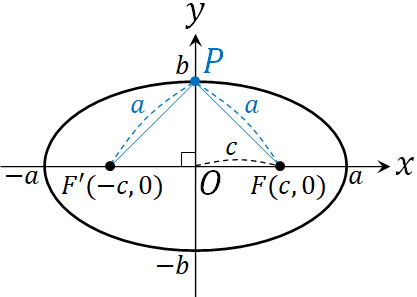
三平方の定理より\(b=\sqrt{a^2-c^2}\)です。そのため、\(a^2-c^2=b^2\)となるのです。そこで、式を以下のように変形しましょう。

\((a^2-c^2)x^2+a^2y^2\)\(=a^2(a^2-c^2)\)

\(b^2x^2+a^2y^2\)\(=a^2b^2\)

\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\)

※\(a>b>0\)の場合

こうして、楕円の方程式を得ることができました。なお、先ほど\(b=\sqrt{a^2-c^2}\)と解説しました。同じように、三平方の定理を利用すると\(c=\sqrt{a^2-b^2}\)とわかります。こうして、焦点の座標を計算できます。

焦点が\(y\)軸上に存在する場合の式

ここまでの解説では、長軸を\(2a\)としました。ただ楕円によっては、長軸が\(2b\)になることもあります。言い換えると、\(b>a>0\)の場合もあります。この場合、焦点は\(x\)軸上ではなく\(y\)軸上に存在することになるため、焦点の座標はF\((0,c)\)、F’\((0,-c)\)となります。

また、焦点の座標は\(c=\sqrt{b^2-a^2}\)です。大きい値から小さい値を引かないと実数を得られないため、こうした式になります。その結果、以下の図を作ることができます。

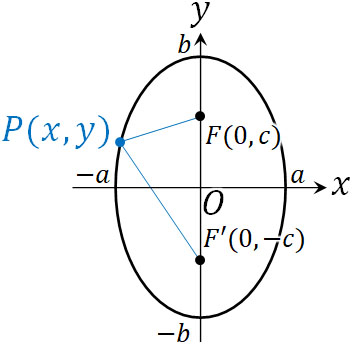
なお長軸は\(2b\)であるため、楕円の方程式は以下のようになります。

\(FP+F’P=2b\)

長軸と短軸の位置関係を把握することにより、楕円の形を描けるようになりましょう。

円と楕円の関係：軌跡を利用して楕円を描く

それでは、円と楕円にはどのような関係があるのでしょうか。以下の問題を解いてみましょう。

円\(x^2+y^2=36\)について、\(x\)軸を基準に\(y\)軸方向へ\(\displaystyle\frac{2}{3}\)に縮小させる場合、どのような図形になりますか。

円上の点をQ\((s,t)\)、縮小後の点をP\((x,y)\)とします。この場合、\(x\)軸の座標は同じなので\(x=s\)です。一方、\(y\)軸では\(\displaystyle\frac{2}{3}\)に縮小するため、\(y=\displaystyle\frac{2}{3}t\)となります。

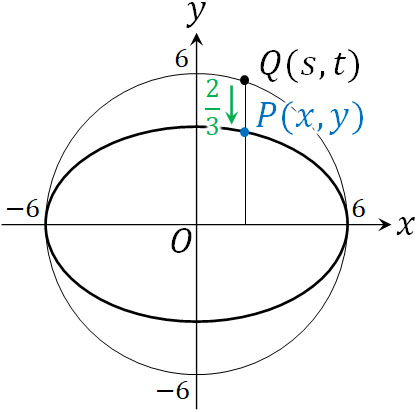
そこで、\(s^2+t^2=36\)に対して\(s=x\)と\(t=\displaystyle\frac{3y}{2}\)を代入しましょう。

\(s^2+t^2=36\)

\(x^2+\displaystyle\frac{9y^2}{4}=36\)

\(\displaystyle\frac{x^2}{36}+\displaystyle\frac{y^2}{16}=1\)

こうして、円を楕円に変換することができました。なお\(y\)軸方向へ\(\displaystyle\frac{2}{3}\)に縮小させたため、\(y\)軸との交点は\(±6\)から\(±4\)へと変化します。楕円というのは、円を\(x\)軸または\(y\)軸方向へ拡大・縮小させた図と考えることもできるのです。

・軌跡を用いて楕円を描く

それでは、軌跡を利用して楕円を描きましょう。以下の問題の答えは何でしょうか。

長さが7の線分ABについて、点Aは\(x\)軸上を動き、点Bは\(y\)軸上を動きます。線分AB上に\(AP=3\)となる点Pをとるとき、点Pの軌跡を求めましょう。

まず、以下のように図を描きましょう。

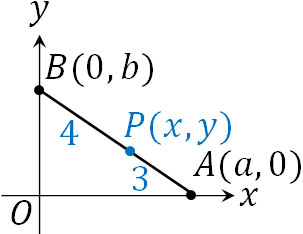
このように図を描くと、点Pは線分ABを\(3:4\)に内分する点であるとわかります。また点Aの座標を\((a,0)\)、点Bの座標を\((0,b)\)とします。線分ABの長さは7であるため、三平方の定理を利用すると以下の式を作れます。

\(a^2+b^2=49\)

次に、点Pの座標を\((x,y)\)とします。前述の通り、点Pは線分ABを\(3:4\)に内分する点です。そのため内分点の公式を利用することにより、以下の式を作れます。

\(x=\displaystyle\frac{4a}{3+4}=\displaystyle\frac{4}{7}a\)
\(y=\displaystyle\frac{3b}{3+4}=\displaystyle\frac{3}{7}b\)

そこで、\(a^2+b^2=49\)に対して\(a=\displaystyle\frac{7}{4}x\)、\(b=\displaystyle\frac{7}{3}y\)を代入しましょう。

\(a^2+b^2=49\)

\(\displaystyle\frac{49x^2}{16}+\displaystyle\frac{49y^2}{9}=49\)

\(\displaystyle\frac{x^2}{16}+\displaystyle\frac{y^2}{9}=1\)

こうして、点Pが描く軌跡を利用することによって楕円の方程式を得ることができました。

双曲線の方程式の概要と決定

先ほど、焦点F\((c,0)\)とF’\((-c,0)\)からの距離の和が一定である場合、楕円となると解説しました。一方で焦点F\((c,0)\)とF’\((-c,0)\)からの距離の差が一定である場合、双曲線となります。

そこで楕円のときと同じように、2点からの距離の差が一定になるように点P\((x,y)\)を取りましょう。このとき、一定の部分を\(2a\)とすると、以下のようになります。

\(|F’P-FP|=2a\)

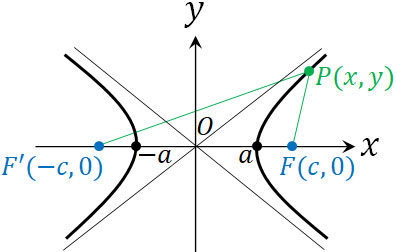
※\(0<a<c\)

一定が\(2a\)となることに意味はありません。楕円のときと同じであればわかりやすいため、ひとまず一定は\(2a\)になると理解しましょう。またFPとF’Pについて、差がマイナスになってもいいようにするために絶対値を加えます。

そこで、楕円のときと同様に計算しましょう。

\(|F’P-FP|=2a\)

\(|\sqrt{(x-c)^2+y^2}\)\(-\sqrt{(x+c)^2+y^2}|\)\(=2a\)

\(\sqrt{(x-c)^2+y^2}\)\(-\sqrt{(x+c)^2+y^2}\)\(=±2a\)

\(\sqrt{(x-c)^2+y^2}\)\(=±2a+\sqrt{(x+c)^2+y^2}\)

\((x-c)^2+y^2\)\(=4a^2\)\(±4a\sqrt{(x+c)^2+y^2}\)\(+(x+c)^2+y^2\)

\(±4a\sqrt{(x+c)^2+y^2}=4a^2+4cx\)

\(±a\sqrt{(x+c)^2+y^2}=a^2+cx\)

次に、両辺を二乗しましょう。

\(±a\sqrt{(x+c)^2+y^2}=a^2+cx\)

\(a^2(x+c)^2+a^2y^2\)\(=a^4+2a^2cx+c^2x^2\)

\(a^2x^2-c^2x^2+a^2y^2\)\(=a^4-a^2c^2\)

\((a^2-c^2)x^2+a^2y^2\)\(=a^2(a^2-c^2)\)

こうして、楕円で計算したときとまったく同じ式を得ることができました。重要なのは、\(0<a<c\)であることです。そこで、両辺にマイナスをかけることで以下のように式を変形しましょう。

\((c^2-a^2)x^2-a^2y^2\)\(=a^2(c^2-a^2)\)

このとき、\(b=\sqrt{c^2-a^2}\)とすると以下の式を作れます。

\((c^2-a^2)x^2-a^2y^2\)\(=a^2(c^2-a^2)\)

\(b^2x^2-a^2y^2\)\(=a^2b^2\)

\(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=1\)

こうして、双曲線の方程式を得ることができました。楕円の方程式と比較すると、違いは\(y\)にマイナスが存在するかどうかです。この違いにより、方程式が楕円を示すのか、それとも双曲線を示すのか変化します。

漸近線と双曲線の関係

ただ、先ほどの式で疑問が思い浮かびます。グラフを確認しても、どこが\(b\)に該当するのかわかりません。そこで、双曲線で\(b\)が何を意味しているのか学びましょう。双曲線では漸近線を利用することになり、漸近線で\(b\)を用います。

前述の通り、\(b=\sqrt{c^2-a^2}\)です。そのため、\(c=\sqrt{a^2+b^2}\)によって焦点の座標を得られます。ただ、焦点がわかってもグラフを正しく描くことはできません。以下のように、どれだけ線の広がりがあるのかわからないからです。

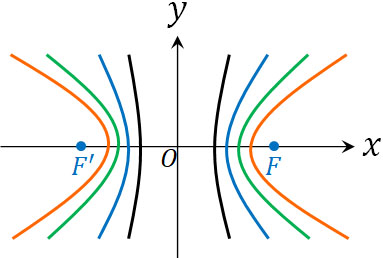
そこで、漸近線を利用しましょう。曲線との距離が近づくものの、接することのない線を漸近線といいます。最も有名な双曲線に反比例があります。反比例の場合、\(x\)軸と\(y\)軸が双曲線になります。

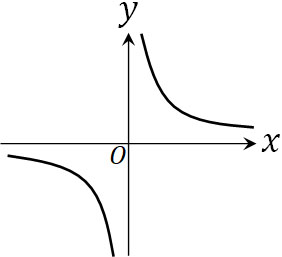
そこで、双曲線を描くために漸近線を図に記載しましょう。証明すると複雑になるので省きますが、双曲線の方程式\(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=1\)について、以下の2つの式が漸近線の式になります。

\(\displaystyle\frac{x}{a}-\displaystyle\frac{y}{b}=0\)
\(\displaystyle\frac{x}{a}+\displaystyle\frac{y}{b}=0\)

こうして漸近線を利用することにより、双曲線を描けるようになります。

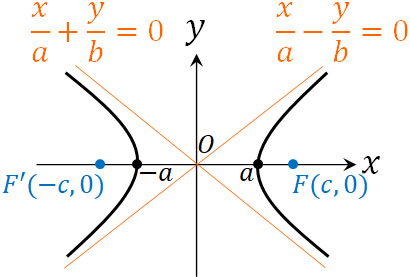
二次曲線の中では、双曲線が最も理解するのが難しいです。そこで、双曲線での\(b\)や漸近線が何を意味しているのか学びましょう。

なお場合によっては、焦点が\(x\)軸ではなく\(y\)軸に存在することもあります。この場合、以下のようになります。

方程式：\(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=\color{red}{-1}\)
焦点：F\((0,c)\)とF’\((0,-c)\)

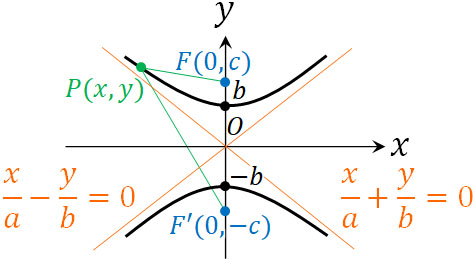
焦点の値は\(c=\sqrt{a^2+b^2}\)であり、漸近線は\(\displaystyle\frac{x}{a}±\displaystyle\frac{y}{b}=0\)です。そのため、焦点の値の計算方法と漸近線の方程式は同じです。焦点が\(y\)軸に存在する場合についても、双曲線を利用できるようになりましょう。

二次曲線の平行移動と計算方法

二次関数や円では、平行移動するときの方程式を学びました。そこで二次曲線（放物線、楕円、双曲線）についても、平行移動させる方法を学びましょう。

方法は二次関数や円の場合と同じです。二次関数や円を\(x\)軸方向に\(a\)、\(y\)軸方向に\(b\)移動させる場合、\(x\)を\((x-a)\)に変え、\(y\)を\((y-b)\)に変えます。例えば\(x^2+y^2~=4\)を\(x\)軸方向に1、\(y\)軸方向に2移動させる場合、円の方程式は以下のようになります。