sine(正弦:sin)・cosine(余弦:cos)・tangent(正接:tan)を学ぶとき、角度の足し算や引き算をすることによって、三角比がどのように変化するのか理解しましょう。
具体的には、以下のときに三角比がどう変わるのか理解するのです。
- \(90°-θ\)
- \(90°+θ\)
- \(180°-θ\)
角度を足したり引いたりするとき、必ず図を描くようにしましょう。そうすれば暗記することなく、三角比がどのように変化するのか理解できるようになります。そこで、角度の変化と三角比の関係を解説していきます。
もくじ
\(90°-θ\)での三角比の関係
三角比でsin・cos・tanを理解した後、角度が変化するときに三角比がどう変化するのか理解しましょう。具体的には、90°からθ(角度)を引いたときの三角比の変化を学ぶのです。
\(0°≦θ≦90°\)のとき、\(90°-θ\)の三角比は以下のようになります。
- \(sin(90°-θ)=cosθ\)
- \(cos(90°-θ)=sinθ\)
- \(tan(90°-θ)=\displaystyle\frac{1}{tanθ}\)
このような関係性になっています。つまり90°からθ(角度)を引くことによって、sineがcosineになったり、tangentが分数になったりするのです。
\(90°-θ\)でsin・cos・tanが変化する理由
それでは、このように\(90°-θ\)によってなぜsin、cos、tanが変化するのでしょうか。先ほどの公式を暗記しても意味がなく、問題を解くことはできません。つまり、公式を覚えてはいけません。その代わり、理由を理解しましょう。
三角比を理解するためには、図を描くことが重要です。例えば、角度がθの三角形を考えてみましょう。以下のようになります。
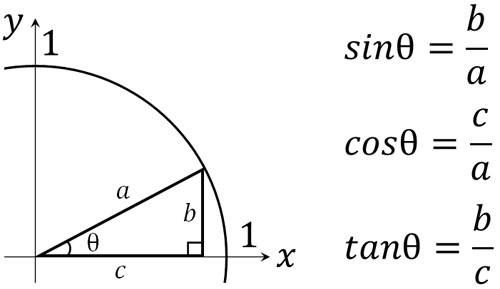
この図については問題なく理解できるはずです。次に、\(90°-θ\)を考えてみましょう。\(90°-θ\)は以下のようになります。
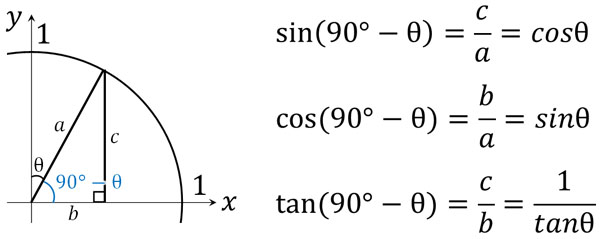
先ほどの図と比較すると、\(sin(90°-θ)=cosθ\)になっていることがわかります。また\(cos(90°-θ)=sinθ\)であり、\(tan(90°-θ)=\displaystyle\frac{1}{tanθ}\)です。
それでは、なぜこの図を描くことができるのでしょうか。この理由を理解するため、以下のように合同な三角形を配置しましょう。
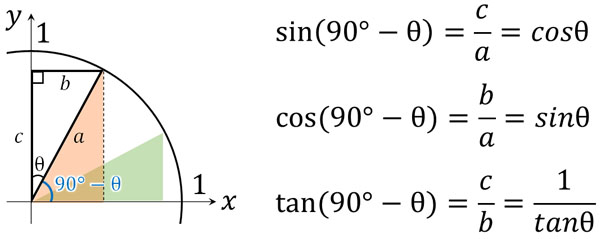
このように図を描くと、θをもつ三角形と\(90°-θ\)をもつ三角形は合同であるとわかります。そのため、辺の長さは同じです。ただ、辺の場所が変わっています。そこで合同な三角形を利用し、\(90°-θ\)を基準とする直角三角形の三角比を探すと、先ほどの公式が成り立ちます。
例えば角度(θ)が30°の場合、\(90°-θ\)は60°です。そのため、以下のようになります。
- \(sin(90°-30°)=sin60°=cos30°\)
- \(cos(90°-30°)=cos60°=sin30°\)
- \(tan(90°-30°)=tan60°=\displaystyle\frac{1}{tan30°}\)
\(sin60°=\displaystyle\frac{\sqrt{3}}{2}\)であり、\(cos30°=\displaystyle\frac{\sqrt{3}}{2}\)です。このように、実際に計算しても公式が成り立つとわかります。
三角比の関係を理解するとき、必ず図を利用しましょう。図がないと、\(90°-θ\)の角度をもつ直角三角形の三角比を理解するのは難しいです。
\(0°≦θ≦180°\)のときの三角比
一方で角度が90°までではなく、\(0°≦θ≦180°\)のときはどのように考えればいいのでしょうか。三角比というのは、辺の比を表します。そのためsinθとcosθの値が1を超えることはありません。sinθやcosθが1を超える場合、斜辺よりも長いたての辺(または横の辺)をもつ直角三角形となりますが、そうした三角形は存在しないのです。
そこで、先ほどと同じように\(x\)座標が1、\(y\)座標が1の半円で考えてみましょう。
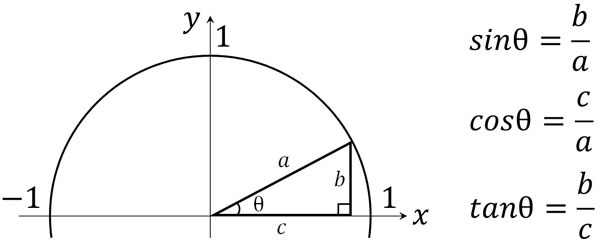
\(0°≦θ≦90°\)のときと異なるのは、\(0°≦θ≦180°\)では、角度が90°を超えると\(x\)座標がマイナスになることです。\(y\)座標は正の値であるものの、\(x\)座標は負の値になることを理解しましょう。
\(90°+θ(0°≦θ≦90°)\)の角度をもつ三角形では、必ず角度が90°を超えます。また\(180°-θ\)の角度をもつ三角形では、一つの角度が90°を超えることがあります。いずれにしても角度が90°よりも大きいとき、\(x\)座標がマイナスになる事実を知っていることが重要になります。
\(90°+θ\)での三角比の関係
まず、\(90°+θ\)をもつ直角三角形で考えてみましょう。以下のように、合同な三角形を作ります。
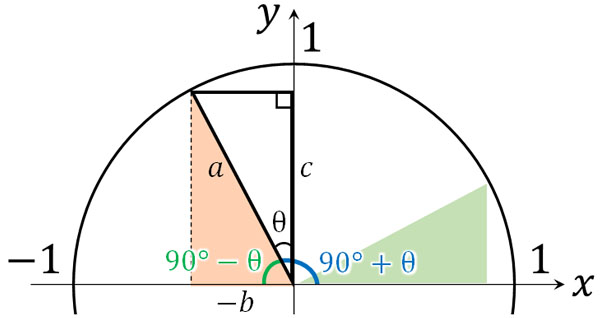
このように図を描くと、角度(θ)に対して90°を加える場合、左側に\(90°-θ\)の角度をもつ合同の直角三角形を作ることができます。そのため\(90°+θ\)では、\(90°-θ\)の角度をもつ直角三角形の三角比を計算することになります。
ただ先ほどとは異なり、\(90°+θ\)では\(x\)軸が負の値になります。そこで、\(x\)軸が負の値であることを考慮して三角比をださなければいけません。
sine(正弦)の値をだすとき、利用する値は斜辺の長さと\(y\)座標(たての辺の長さ)です。これらの値はどちらもプラスであるため符号は変わりません。
一方でcosine(余弦)をだすとき、斜辺の長さと横の辺の長さを利用します。角度が90°よりも大きい場合、図を確認すると、\(x\)座標(横の辺の長さ)は負の値になっています。そのため、\(cos(90°+θ)\)を\(cos(90°-θ)\)に変えるとき、マイナスを加えるようにしましょう。
同じようにtangent(正接)をだすとき、\(x\)座標(横の辺の長さ)と\(y\)座標(たての辺の長さ)を利用します。\(x\)座標はマイナスであるため、\(tan(90°+θ)\)を\(tan(90°-θ)\)に変えるとき、マイナスを加えなければいけません。
そのため、以下のようになります。
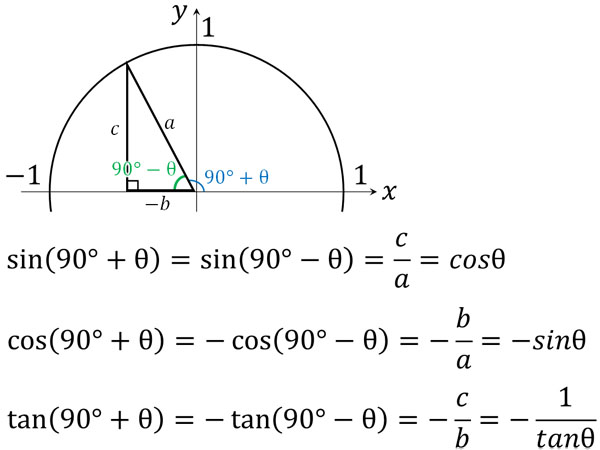
三角比で\(90°+θ\)というのは、\(90°-θ\)の角度をもつ直角三角形の三角比を出すのと意味が同じです。ただ\(90°-θ\)の角度をもつ直角三角形と異なり、\(x\)座標がマイナスになります。そのため、cosineとtangentの符号がマイナスになります。cosineとtangentは\(x\)座標を利用して三角比を出すからです。
\(180°-θ\)での三角比の関係
次に、\(180°-θ\)の角度をもつ直角三角形を考えてみましょう。\(180°-θ\)では、以下の図を描くことができます。
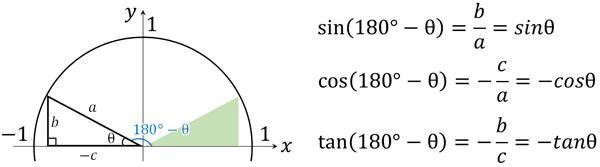
\(180°-θ\)の角度はθと同じです。そのため\(180°-θ\)の三角比を出すというのは、角度θをもつ直角三角形を計算するのと意味が同じです。斜辺の長さと\(y\)座標(たての辺の長さ)が両方とも正の値であるため、\(sin(180°-θ)=sinθ\)となります。
ただ先ほど解説した通り、\(x\)座標(下の辺の長さ)は負の値になります。そのためcosineやtangentの値を出すとき、\(180°-θ\)では答えがマイナスになります。そのため、以下の関係が成り立ちます。
- \(sin(180°-θ)=sinθ\)
- \(cos(180°-θ)=-cosθ\)
- \(tan(180°-θ)=-tanθ\)
図を描くことによって、なぜこれらの公式が有効なのか理解できるようになります。実際に問題を解くとき、必ず簡単な図を描くことによって答えを出すようにしましょう。そうしなければ、頻繁に計算ミスをしてしまいます。
実際に三角比の計算を行う
それでは、実際に三角比の値を出しましょう。例えば\(0°<θ<180°\)のとき、以下の答えは何でしょうか。
- \(sinθ=\displaystyle\frac{1}{3}\)のとき、cosθとtanθの値は?
sinθの値がわかれば、以下の公式を利用することによってcosθとtanθの値を出すことができます。
- \(sin^2θ+cos^2θ=1\)
- \(tanθ=\displaystyle\frac{sinθ}{cosθ}\)
そこで、\(sin^2θ+cos^2θ=1\)に代入しましょう。以下のようになります。
\(sin^2θ+cos^2θ=1\)
\(\left(\displaystyle\frac{1}{3}\right)^2+cos^2θ=1\)
\(cos^2θ=\displaystyle\frac{8}{9}\)
\(cosθ=±\displaystyle\frac{2\sqrt{2}}{3}\)
次にtanθの値を出しましょう。
\(0°<θ<90°\)のとき、cosθは正の値になります。そのため、\(cosθ=\displaystyle\frac{2\sqrt{2}}{3}\)です。そこで、\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)に代入しましょう。
\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)
\(tanθ=sinθ÷cosθ\)
\(tanθ=\displaystyle\frac{1}{3}÷\displaystyle\frac{2\sqrt{2}}{3}\)
\(tanθ=\displaystyle\frac{1}{2\sqrt{2}}\)
一方、\(90°<θ<180°\)のとき、cosθは負の値になります。そのため、\(cosθ=-\displaystyle\frac{2\sqrt{2}}{3}\)です。またtanθも負の値になるため、先ほどの答えに-1をかけましょう。そのため、\(tanθ=-\displaystyle\frac{1}{2\sqrt{2}}\)です。
こうして、三角比の値を出すことができます。
三角比での不等式
ここまでの内容を理解すれば、三角比で不等式を利用した式を計算できるようになります。不等式の問題を解く場合、必ず図を描く必要があります。図を描かない場合、非常に高い確率で計算ミスをするからです。
例えば\(0°<θ<180°\)のとき、以下の不等式を満たすθの範囲は何でしょうか。
- \(sinθ>\displaystyle\frac{\sqrt{3}}{2}\)
- \(cosθ<\displaystyle\frac{\sqrt{3}}{2}\)
- \(tanθ<1\)
不等式の問題を解くとき、まずはイコールの記号を利用して角度を求めましょう。その後、不等式を満たす角度を見つけるのです。
(1)
\(sinθ=\displaystyle\frac{\sqrt{3}}{2}\)を解くと、角度(θ)は60°とわかります。sinθでは、角度が大きくなると値が大きくなります。sinθでは、直角三角形のたての長さが分子になります。斜辺の長さは変わらないものの、角度が大きくなれば\(y\)座標(たての長さ)が増えるからです。
ただ90°を超えると、角度が大きくなるにしたがってsinθの値は小さくなります。\(y\)座標(たての長さ)が小さくなるからです。そのため、以下の図を作ることができます。
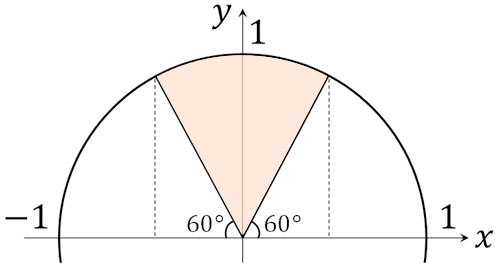
このように図にすると、\(60°<θ<120°\)が答えであるとわかります。
(2)
\(cosθ=\displaystyle\frac{\sqrt{3}}{2}\)を解くと、θは30°です。このとき角度が大きくなるとcosθの値は小さくなります。理由としては、cosθでは\(x\)軸の座標(横の線の長さ)が分子になるからです。また角度が90°を超えると、cosθの値はマイナスになります。
そのため\(cosθ<\displaystyle\frac{\sqrt{3}}{2}\)を満たす角度としては、以下の図を描けます。
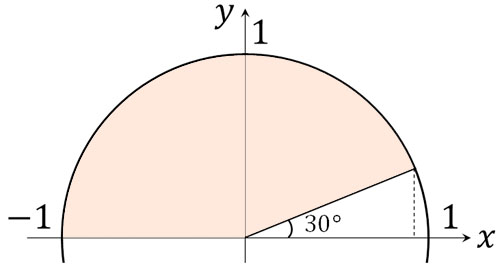
そのため、\(30°<θ<180°\)が答えになります。
(3)
\(tanθ=1\)を解くと、θは45°です。\(tanθ<1\)を満たすためには、角度は45°よりも大きければいいのでしょうか、それとも小さければいいのでしょうか。仮にθを60°とすると、\(tanθ=\sqrt{3}\)です。つまり角度が45°よりも大きくなると、tanθの値は1よりも大きくなります。
そのため\(tanθ<1\)を満たすためには、角度は45°よりも小さくなる必要があります。
また注意点として、角度が90°よりも大きくなると、tanθの値はマイナスになります。つまり90°よりも角度が大きい場合、必ず\(tanθ<1\)を満たします。そのため、以下の図を描くことができます。
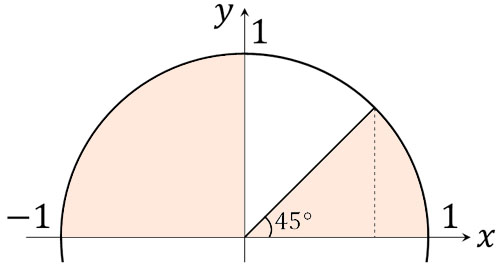
図を見ると、\(0°<θ<45°,90°<θ<180°\)が答えになります。
正接は直線の傾きになる
なお、三角比でtanθを利用するのはどのような意味があるのでしょうか。図を確認すると、tanθは直線(一次関数)の傾きになります。直線の傾きは\(x\)の増加量と\(y\)の増加量を利用して計算します。これが、tanθの値が一次関数の傾きになる理由です。
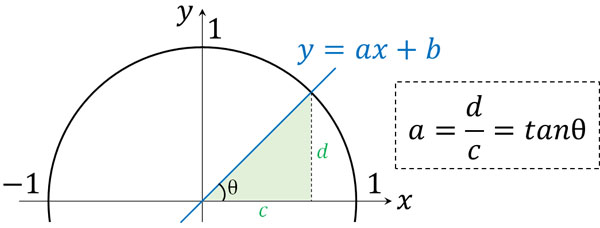
tanθの値を出すというのは、一次関数の傾きを出すのと意味が同じであることを理解しましょう。これを理解すれば、直線が交わるときの角度を計算できます。例えば、以下の答えは何でしょうか。
- \(y=x\)と\(y=-\displaystyle\frac{1}{\sqrt{3}}x\)のなす角を求めましょう。
この問題を解くため、必ず図を描きましょう。まず、\(y=x\)の傾きは1です。\(tanθ=1\)になるためには、角度が45°になる必要があります。
また\(y=-\displaystyle\frac{1}{\sqrt{3}}x\)の傾きは\(-\displaystyle\frac{1}{\sqrt{3}}\)です。\(tanθ=-\displaystyle\frac{1}{\sqrt{3}}\)になるためには、角度が150°である必要があります。そのため、以下の図を作ることができます。
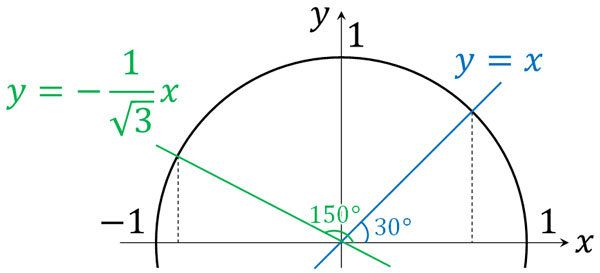
このように図を作ると、2つの直線のなす角は60°と120°であるとわかります。tanθが図形でどのような役割があるのか理解しましょう。
角度の変化によるsinθ、cosθ、tanθの値を学ぶ
三角比では、角度が変化することによってsinθ、cosθ、tanθの値がどのように変化するのか理解する必要があります。これを学ぶとき、必ず図を作るようにしましょう。
図を描けば90°-θや90°+θ、180°-θのとき、三角比の値がどのように変わるのかわかります。公式を覚えるのではなく、図を利用することで、なぜ三角比の値が変化するのか理解するようにしましょう。そうしなければ、応用問題で答えを得ることができません。
また計算ミスをなくすためには、簡単な図を描くことによって答えを出しましょう。三角比は図形の計算であるため、図の利用は必須です。
ここまでの内容を理解して、角度の変化に伴い、sinθ、cosθ、tanθの値を答えられるようにしましょう。






