二次方程式を解くとき、答えが整数で出ないことがあります。その場合、解の公式を使います。解の公式を利用すれば、答えに平方根が含まれていても答えを出すことができます。
二次方程式の解の公式を覚えていれば、判別式を利用することができます。二次方程式がいくつの答えをもつのか判断するための式が判別式です。
判別式を利用すれば二次方程式だけでなく、二次関数での答えの数を判断できるようになります。つまり、その二次関数がどのようなグラフを描くのか判断できるのです。また判別式を利用すれば、放物線と直線が交点をもつかどうかを調べることができます。
どのようにして二次方程式の解の公式を利用し、実数解の個数を判断するのか解説していきます。
もくじ
二次方程式の答えを解の公式で出す
二次方程式の答えを出すとき、最も一般的な方法は因数分解です。因数分解することによって、整数の答えを出すことができます。
ただ二次方程式を因数分解できないケースはどうすればいいでしょうか。その場合、解の公式を利用します。中学校で平方根や二次方程式の解の出し方を学んでいる場合、二次方程式の解の公式をすでに習っています。以下が解の公式です。
$$x={-b\pm\sqrt{b^2-4ac}\over2a}$$
この公式は必ず覚えなければいけません。覚えていない場合、二次方程式の問題を解けないからです。解き方としては、数字を代入するだけです。例えば、以下の二次方程式の答えは何でしょうか。
- \(2x^2+3x-4=0\)
\(ax^2+bx-c=0\)と\(2x^2+3x-4=0\)を比べると、\(a=2\)、\(b=3\)、\(c=-4\)です。そこで、数字を解の公式に代入しましょう。以下のようになります。
\(x=\displaystyle\frac{-b±\sqrt{b^2-4ac}}{2a}\)
\(x=\displaystyle\frac{-3±\sqrt{3^2-4×2×(-4)}}{2×2}\)
\(x=\displaystyle\frac{-3±\sqrt{9+32}}{4}\)
\(x=\displaystyle\frac{-3±\sqrt{41}}{4}\)
こうして、二次方程式の答えを出すことができます。
二次方程式の実数解の個数:判別式
なお二次方程式の解の公式を覚えている場合、二次方程式がいくつ答えをもつのか理解できるようになります。これを判別式(\(D\))と呼びます。以下が判別式です。
- \(D=b^2-4ac\)
判別式を覚える必要はありません。解の公式を確認すると、以下の部分が判別式になります。
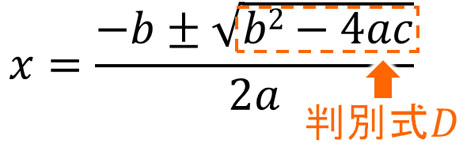
判別式\(D\)というのは、解の公式の中でルート内にある式を指します。それでは、判別式\(D\)を学ぶことがなぜ重要なのでしょうか。それは、判別式を確認することによって二次方程式がもつ答えの数を知ることができるからです。
判別式の答えがプラスなのかマイナスなのかによって、以下のように実数解の個数が変わります。
- 判別式\(D>0\):異なる2つの実数解をもつ
- 判別式\(D=0\):1つの実数解をもつ(重解)
- 判別式\(D<0\):実数解をもたない
このように、判別式を確認することで答えの数がわかります。
なぜ判別式で実数解の個数がわかるのか
それでは、なぜ判別式を利用することによって答えの数がわかるのでしょうか。この理由について、平方根の性質を思い出せば理解できます。
平方根を利用する場合、ルート内の数字がマイナスになってはいけません。例えば、\(\sqrt{-2}\)という数字は存在しません。そこで解の公式をみると、ルートの中に\(b^2-4ac\)があります。つまり\(b^2-4ac\)の答えがマイナスの場合、解の公式を利用して答えを出すことができません。
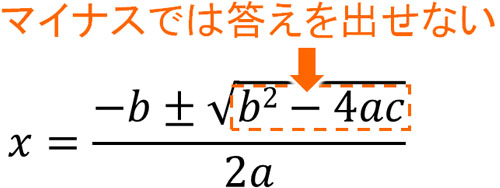
判別式\(D\)の答えがマイナスの場合は解の公式で答えが存在しないため、二次方程式は答えをもちません。一方で判別式\(D\)がプラスの場合、解の公式を利用することで2つの異なる答えを出すことができます。
それでは、判別式を利用して\(D=0\)となる場合はどのように考えればいいのでしょうか。\(D=0\)では\(b^2-4ac=0\)になります。つまり、解の公式で\(±\)の部分が消えます。
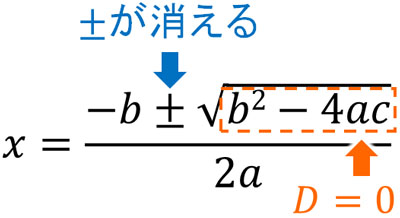
\(±\)が消えるため、答えは一つのみになります。これが、\(D=0\)の場合に答えが一つになる理由です。なお答えが一つの場合、重解と呼ばれます
解の公式を利用できるのは二次方程式
なお、解の公式を一次方程式で利用してはいけません。二次方程式(\(a≠0\))で解の公式を利用することができます。例えば、以下の式で2つの実数解をもつ\(a\)の範囲は何でしょうか。
- \(ax^2+(2a-1)x+a=0\)
判別式\(D>0\)を利用すると、以下のようになります。
\(D=b^2-4ac>0\)
代入すると
\((2a-1)^2-4×a×a>0\)
\((4a^2-4a+1)-4a^2>0\)
\(-4a+1>0\)
\(-4a>-1\)
\(a<\displaystyle\frac{1}{4}\)
ただ、答えを\(a<\displaystyle\frac{1}{4}\)にすると間違いです。なぜ間違いになるのでしょうか。その理由として、\(a=0\)のときに先ほどの式が一次方程式になってしまうからです。そのため、\(a=0\)を除かなければいけません。
・\(a=0\)の場合
\(ax^2+(2a+1)x+a=0\)
\(x=0\)
方程式は一つの解をもち、二つの解をもちません。そのため、\(a≠0\)となります。つまり、答えは以下になります。
\(a<0,0<a<\displaystyle\frac{1}{4}\)
グラフの二次関数、判別式の関係
次に二次方程式ではなく、二次関数で判別式を利用しましょう。二次関数ではグラフを描くことができます。また判別式を利用すれば、二次関数のグラフが\(x\)軸との交点をいくつもつのかわかるようになります。
具体的には以下のようになります。
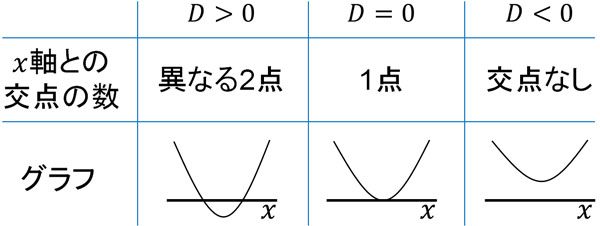
なぜ、このように判断できるのでしょうか。この理由を理解するため、二次関数の式を確認しましょう。二次関数は以下の式で表されます。
- \(y=ax^2+bc+c\)
次に\(y=0\)を代入してみましょう。そうすると、\(ax^2+bc+c=0\)になります。\(ax^2+bc+c=0\)は二次方程式であり、判別式を利用することによって実数解がいくつあるのか調べることができます。
二次関数で\(y=0\)というのは、\(x\)軸を表します。\(x\)軸上にある数字はすべて\(y=0\)になります。また\(D>0\)であれば、\(y=0\)のとき2つの答えがあることを意味します。そのため二次関数で判別式を利用する場合、\(y=0\)のとき、答えがいくつあるのか調べることができます。
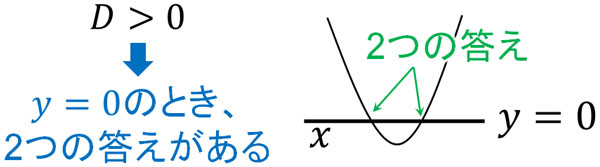
一方で\(D=0\)の場合、\(y=0\)のときに一つの答えが出ます。つまり、二次関数は\(x\)軸上で接します。また\(D<0\)の場合、\(y=0\)のときに答えが出ません。つまり、二次関数は\(x\)軸との交点がありません。
・\(x\)軸に接する場合の答えの出し方
それでは、実際に問題を解いてみましょう。以下の二次関数について、\(x\)軸に接する\(k\)の値は何でしょうか。
- \(x^2+(k-3)x+k\)
\(x\)軸に接するというのは、\(x\)軸との交点が1つであることを意味します。つまり、判別式を利用すると\(D=0\)になります。そこで、\(D=0\)になる\(k\)を求めましょう。以下のようになります。
\(D= b^2-4ac=0\)
代入すると
\((k-3)^2-4×1×k=0\)
\((k^2-6k+9)-4k=0\)
\(k^2-10k+9=0\)
\((k-1)(k-9)=0\)
こうして、\(k=1\)または\(k=9\)のとき、二次関数は\(x\)軸で接するようになります。
放物線と直線の共有点とその個数
ここまでの内容を理解すれば、放物線(二次関数)と直線(一次関数)との共有点の個数や座標を見つけることができます。
二次関数と一次関数の交点を見つける方法としては、連立方程式を解けばいいです。例えば、次の二次関数と一次関数が共有点をもつとき、\(k\)の範囲を求めましょう。
- \(y=x^2\)
- \(y=-x+k\)
この問題を解くため、以下の連立方程式を作ります。
\(\begin{eqnarray} \left\{\begin{array}{l}y=x^2\\y=-x+k\end{array}\right.\end{eqnarray}\)
そこで、\(y=-x+k\)を\(y=x^2\)に代入しましょう。以下のようになります。
\(x^2=-x+k\)
\(x^2+x-k=0\)
この二次方程式が解をもつ場合、二次関数と一次関数は共有点をもちます。解をもつためには、判別式は\(D≧0\)である必要があります。そのため判別式を利用して以下のように計算します。
\(D=b^2-4ac≧0\)
代入すると
\(1^2-4×1×(-k)≧0\)
\(1+4k≧0\)
\(k≧-\displaystyle\frac{1}{4}\)
こうして、\(k≧-\displaystyle\frac{1}{4}\)が答えであるとわかります。
なぜ代入によって放物線と直線の交点がわかるのか
それでは、なぜ代入することによって放物線と直線の交点を求めることができるのでしょうか。これを理解するため、先ほどの連立方程式を確認しましょう。
\(\begin{eqnarray} \left\{\begin{array}{l}y=x^2\\y=-x+k\end{array}\right.\end{eqnarray}\)
その後、\(y=-x+k\)を\(y=x^2\)に代入しました。また連立方程式で代入するというのは、引き算をするのと意味が同じです。以下のように、引き算をすることによって\(y\)を消すことができます。
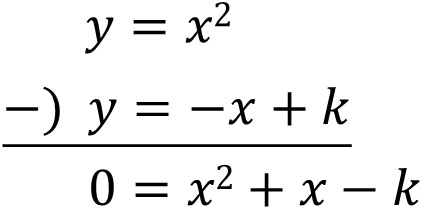
そこで、\(y=x^2\)の関数を\(y=A\)としましょう。また、\(y=-x+k\)の関数を\(y=B\)としましょう。そうすると、以下の新たな関数を作ることができます。
- \(y’=A-B\)
このように新たな関数を作ることによって、ここまで学んできた二次関数のグラフを描くことができます(下図の右側)。
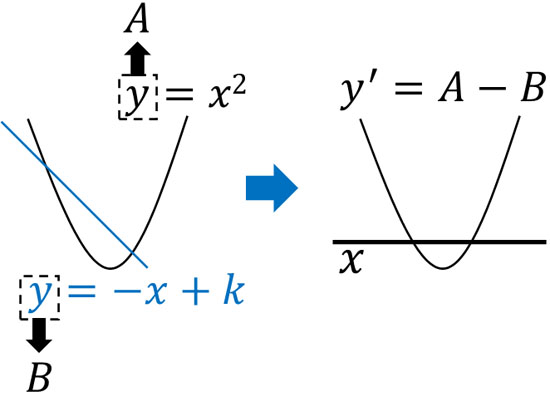
また\(A-B=0(y’=0)\)となる場合、\(A=B\)となります。\(A=B\)というのは、関数Aと関数Bの座標が同じになることを意味します。同じ座標というのは、つまり交点を意味します。
そこで\(y’=A-B\)の関数について、\(y’=0\)になる条件を探します。\(y’=0\)というのは、\(y’=A-B\)の関数が\(x\)軸と共有点をもつことを意味します。そのため判別式を利用することによって、\(y=-x+k\)と\(y=x^2\)が交点をもつ条件を求めることができます。
二次方程式と二次関数で判別式を利用する
二次方程式の答えを出す方法の一つとして解の公式があります。解の公式は式の中に平方根をもちます。そのためルート内の数字がマイナスの場合、その二次方程式は解をもちません。
この性質を利用して、私たちは判別式\(D\)を利用します。\(D>0\)の場合、2つの異なる解をもちます。また\(D=0\)の場合、答えは1つです。一方で\(D<0\)の場合、解はありません。判別式がプラスなのかマイナスなのかによって、答えの数が変わります。
これらの内容を学べば、二次関数で判別式を利用できるようになります。二次関数ではグラフを描きます。\(y=0\)の場合、二次方程式と同じ式になります。そのため、二次関数で判別式を利用することで\(x\)軸との交点の数を見分けるようにしましょう。
二次関数で判別式を利用するケースは多いです。どのようなとき、二次方程式や二次関数で答えが存在するのか判別式を用いて判断しましょう。