関数の極限：極限値の条件や解き方、はさみうちの原理

関数について、特定の値へ極限まで近づけるとき、どのような答えを得られるのか計算できるようになりましょう。

例えば、分数では分母が0になることはありません。ただ関数の極限では、分母が0になる極限の計算がひんぱんに出題されます。なお考え方は数列の極限と同じであり、数列の極限を理解している場合、関数の極限を理解するのは容易です。

また関数の極限では、はさみうちの原理を利用できます。数列の極限と同じ方法により、答えを計算しましょう。

それでは、どのように考えて関数の極限を計算すればいいのでしょうか。分母が0になる場合であっても、極限を利用する場合は答えを得ることができます。そこで、計算方法を解説していきます。

1 特定の値に極限まで近づける関数の計算
- 1.1 \(x\)を無限大に大きくする
2 極限値の条件を利用して関数の係数を得る
- 2.1 関数の一方からの極限と答えの違い
- 2.2 関数の極限とはさみうちの原理
3 関数の極限を計算する

特定の値に極限まで近づける関数の計算

関数で特定の値に極限まで近づける場合、関数へ値を代入するのとほぼ意味が同じです。例えば\(\displaystyle \lim_{ x \to 2 } (x^2-3)\)は\(f(x)=x^2-3\)に2を代入するのと意味が同じであり、答えは1です。

ただ、この例だと計算が非常に簡単です。そのため、関数の極限では分母が0になる計算を学びます。極限というのは、特定の値へ極限まで近づけるものの、実際に分母が0になるわけではありません。そのため、一見すると分母が0になると思えたとしても、約分することで分母が0になるのを防げるケースがあります。

例題として、以下の問題を解いてみましょう。

\(\displaystyle \lim_{ x \to 2 } \displaystyle\frac{x^2-3x+2}{x-2}\)

\(x\)に2を代入すると\(\displaystyle\frac{0}{0}\)となります。そこで、以下のように因数分解することで分母を消しましょう。

\(\displaystyle \lim_{ x \to 2 } \displaystyle\frac{x^2-3x+2}{x-2}\)

\(=\displaystyle \lim_{ x \to 2 } \displaystyle\frac{(x-2)(x-1)}{x-2}\)

\(=\displaystyle \lim_{ x \to 2 } (x-1)\)

\(=1\)

前述の通り、\(x\)は2に近づくものの2でありません。\(x-2\)は0ではないため、分子と分母を\(x-2\)で割ることができるのです。

\(x\)を無限大に大きくする

なお、\(x\)を無限大に大きくするときの計算をしなければいけないこともあります。この場合、最も大きい係数を利用して式を変形します。例えば、\(\displaystyle \lim_{ x \to \infty } (x^2-5x+2)\)は以下のように計算します。

\(\displaystyle \lim_{ x \to \infty } (x^2-5x+2)\)

\(=\displaystyle \lim_{ x \to \infty } x^2\left(1-\displaystyle\frac{5}{x}+\displaystyle\frac{2}{x^2}\right)\)

\(=∞(1-0+0)\)

\(=∞\)

計算方法は数列の極限と同じです。そのため数列の極限を学んでいる場合、計算方法は既に知っていることになります。

極限値の条件を利用して関数の係数を得る

それでは、極限値の条件を利用して関数の係数を計算しましょう。以下の問題の答えは何でしょうか。

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a\sqrt{x+3}-b}{x-1}=2\)が成り立つとき、\(a\)と\(b\)を求めましょう。

\(x\)に1を代入すると分母が0になります。ただ答えは2であるため、約分できなければいけません。言い換えると、\(x\)に1を代入することで分子の答えが0になる必要があります。この場合、分子と分母を\(x-1\)で割ることができます。

\(\displaystyle \lim_{ x \to 1 } (a\sqrt{x+3}-b)=0\)であるため、以下のように計算しましょう。

\(\displaystyle \lim_{ x \to 1 } (a\sqrt{x+3}-b)=0\)

\(2a-b=0\)

\(b=2a\)

そこで\(b=2a\)を代入すると、以下のように計算できます。

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a\sqrt{x+3}-b}{x-1}=2\)

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a\sqrt{x+3}-2a}{x-1}=2\)

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a(\sqrt{x+3}-2)}{x-1}=2\)

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a(x+3-4)}{(x-1)(\sqrt{x+3}+2)}=2\)

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a(x-1)}{(x-1)(\sqrt{x+3}+2)}=2\)

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{a}{\sqrt{x+3}+2}=2\)

\(\displaystyle\frac{a}{4}=2\)

\(a=8\)

\(a=8\)であるため、\(b=16\)です。こうして、関数の係数を得ることができました。

関数の一方からの極限と答えの違い

なお極限の計算をするとき、どちら側から値に近づくのかによって答えが変化するケースがあります。わかりやすい例は分数関数です。分数関数では、プラス側とマイナス側について、どちら側から値に近づくのかによって答えが変化します。

このとき\(\displaystyle \lim_{ x \to 1+0 }\)であれば、1.00001のように、1に限りなく近いものの、1よりも大きい値を指します。一方で\(\displaystyle \lim_{ x \to 1-0 }\)であれば、1に限りなく近いものの、1よりも小さい値を指します。それでは、以下の式の答えは何でしょうか。

\(\displaystyle \lim_{ x \to 1+0 } \displaystyle\frac{x+3}{x-1}\)

分子はプラスの値であり、分母はプラスの値です。そのため、\(\displaystyle \lim_{ x \to 1+0 } \displaystyle\frac{x+3}{x-1}=∞\)が正解です。一方、以下の問題の答えは何でしょうか。

\(\displaystyle \lim_{ x \to 1-0 } \displaystyle\frac{x+3}{x-1}\)

この場合、分子はプラスの値であり、分母はマイナスの値です。そのため、\(\displaystyle \lim_{ x \to 1+0 } \displaystyle\frac{x+3}{x-1}=-∞\)となります。このような答えを得られる理由としては、以下のように分数関数のグラフを描けば容易に理解できます。

\(\displaystyle\frac{x+3}{x-1}=\displaystyle\frac{4}{x-1}+1\)

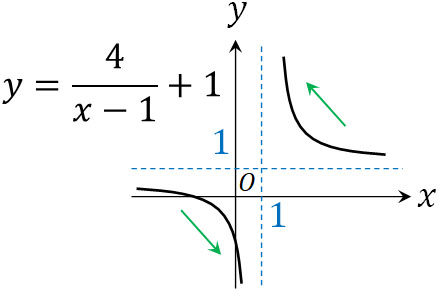
関数の極限では、プラスとマイナスのどちら側から近づくのかによって答えが変わるケースがある事実を学びましょう。

関数の極限とはさみうちの原理

数列の極限では、はさみうちの原理を利用することによって答えを得ることができます。これは、関数の極限も同様です。極限の計算を直接するのが難しい場合、はさみうちの原理を利用することによって答えを得ましょう。

それでは、\(\displaystyle \lim_{ x \to \infty } \displaystyle\frac{sinx}{x}\)の答えは何でしょうか。

\(-1≦sinx≦1\)であるため、\(-\displaystyle\frac{1}{x}≦\displaystyle\frac{sinx}{x}≦\displaystyle\frac{1}{x}\)です。そのため、\(x\)の値を無限大に大きくすると左辺も右辺も0になります。こうして、\(\displaystyle \lim_{ x \to \infty } \displaystyle\frac{sinx}{x}=0\)とわかります。

数列の極限で利用するはさみうちの原理は関数の極限でも利用することができます。