一次式と余りの関係を表す定理に剰余の定理があります。新たな内容ではなく、既にあなたが知っている事実を定理にした内容が剰余の定理です。
ただ、剰余の定理を知っていないと問題を解けないことが多いです。そこで、一次式と商、余りの関係を学ばなければいけません。これらの関係性を理解することにより、値を代入するときに得られる余りがわかります。
また、剰余の定理で余りがゼロになるとき、因数定理を利用できます。特に高次式の因数分解をするとき、因数定理が役に立ちます。
それでは、どのように剰余の定理と因数定理を利用すればいいのでしょうか。剰余の定理と因数定理の利用法を解説していきます。
もくじ
一次式の割り算と余りの関係
まず、剰余の定理とは何かを学びましょう。わり算をすると、余りを得ることができます。一次式を利用して割り算をするとき、余りの数を容易に得られる方法が剰余の定理です。
以下が剰余の定理です。
- 整式\(P(x)\)に対して一次式\((x-a)\)で割るとき、余りは\(P(a)\)となる。
なお、一次式として\((x-a)\)を利用するのではなく、より一般的な一次式として\((ax+b)\)を利用することは多いです。この場合、剰余の定理を利用して以下のように表すことができます。
- 整式\(P(x)\)に対して一次式\((ax+b)\)で割るとき、余りは\(P\left(-\displaystyle\frac{b}{a}\right)\)となる。
つまり余りを得るとき、整式に対して割り算をする必要はありません。\(x\)に値を代入することによって、余りを得ることができます。それでは、以下の問題の答えは何でしょうか。
- \(P(x)=x^2+ax+4\)を\(x+2\)で割ると3余ります。\(a\)の値は何ですか。
剰余の定理を利用すると、\(x=-2\)を代入したとき、3が余ることになります。つまり、\(P(-2)=3\)です。そこで、以下のように計算しましょう。
\(P(-2)=4-2a+4=3\)
\(-2a=-5\)
\(a=\displaystyle\frac{5}{2}\)
こうして、\(a=\displaystyle\frac{5}{2}\)とわかりました。一次式の割り算をするとき、剰余の定理を利用することで余りの数を得ることができるのです。
商、余りを式で表す:剰余の定理の証明
それでは、剰余の定理は何を意味しているのでしょうか。先ほど記した剰余の定理に関する公式を覚える必要はなく、剰余の定理の意味を学びましょう。
割り算をするとき、必ず割る数、商、余りがあります。商を\(Q(x)\)、余りを\(R\)とすると、整式\(P(x)\)と一次式\((ax+b)\)との関係は以下のようになります。
- \(P(x)=(ax+b)Q(x)+R\)
この式を作れることについては、問題なく理解できると思います。このとき、\(x=-\displaystyle\frac{b}{a}\)を代入すると、\((ax+b)=0\)になります。つまり、以下のようになります。
- \(P\left(-\displaystyle\frac{b}{a}\right)=R\)
こうして、整式\(P(x)\)に対して一次式\((ax+b)\)で割るとき、余り\(R\)は\(P\left(-\displaystyle\frac{b}{a}\right)\)になると証明することができました。剰余の定理の証明は非常に簡単であり、新たな内容を学んでいるわけではありません。
つまり剰余の定理というのは、「一次式(割る数)が0となる値を\(P(x)\)に代入するときに得られる余り」を指します。
一次式が0になればいいため、一次式\((x-a)\)で割るとき、\(x-a=0\)となる\(x\)を\(P(x)\)へ代入すればいいです。つまり、一次式\((x-a)\)で割るときの余りを得たい場合、\(P(a)\)を計算しましょう。
また一次式\((ax+b)\)で割るとき、\(ax+b=0\)となる\(x\)を\(P(x)\)へ代入しましょう。そのため、\(P\left(-\displaystyle\frac{b}{a}\right)\)を計算します。これが剰余の定理です。剰余の定理が何を意味しているのか学べば、公式を覚える必要はないとわかります。
例えば\(P(x)=x^2+ax+4\)を\(2x+3\)で割る場合、以下のように表すことができます。
- \(P(x)=(2x+3)Q(x)+R\)
\(2x+3=0\)の解は\(-\displaystyle\frac{3}{2}\)です。そのため、\(P\left(-\displaystyle\frac{3}{2}\right)\)によって余り\(R\)を得ることができます。剰余の定理について本質を学べば、公式を覚える必要はありません。
因数定理:余りが0の場合、因数分解できる
先ほど、\(P(x)\)へ代入することによって余りを計算できることを解説しました。それでは一次式\((x-a)\)で割るとき、\(P(a)=0\)の場合はどのように考えればいいのでしょうか。
\(P(a)=0\)の場合、余りがないことを意味しています。つまり\((x-a)\)は\(P(x)\)の因数です。言い換えると、\((x-a)\)を利用して因数分解することができます。これが因数定理です。
例えば、\(x^2+3x+2\)の因数分解はどのようにすればいいでしょうか。これまでの知識を利用して、以下のように因数分解できます。
- \(x^2+3x+2=(x+2)(x+1)\)
このとき、因数定理を利用して因数分解することもできます。\(P(x)=x^2+3x+2\)について、\(x\)に代入することで答えが0になる値を見つけましょう。そうすると、\(P(-1)=0\)となります。\(x=-1\)、つまり\(x+1=0\)となるため、\(P(x)\)は\(x+1\)を因数にもちます。
このように考え、因数定理を利用することで因数分解できるようになります。
高次式の因数分解を行う
二次方程式の場合、因数定理を利用せずに因数分解するのが一般的です。一方で三次式や四次式など、高次式では因数分解が大変です。そこで因数定理を利用して因数分解しましょう。因数定理を利用すれば、どの式が因数になるのか容易に判断できます。
それでは、以下の式を因数分解しましょう。
- \(x^3+4x^2+x-6\)
\(x\)に何を代入すると、答えが0になるでしょうか。ランダムに値を代入することにより、答えが0になるケースを見つけましょう。
\(P(x)=x^3+4x^2+x-6\)について、\(P(1)=0\)になるとわかります。\(x=1\)を変形すると、\(x-1=0\)です。つまり、\(P(x)\)は\(x-1\)を因数にもちます。そこで\(x-1\)を利用し、係数が合うように因数分解しましょう。
因数分解するとき、以下のように割り算をすることで商を得ましょう。
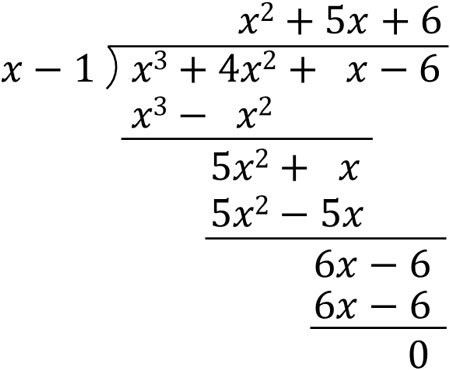
こうして、以下のように因数分解することができます。
\(x^3+4x^2+x-6=\)\((x-1)(x^2+5x+6)\)
なお、この式をさらに因数分解しましょう。
\((x-1)(x^2+5x+6)=\)\((x-1)(x+2)(x+3)\)
ヒントなしで高次式の因数分解をするのは難しいです。そこで因数定理を利用して、どの一次式を利用して割り算が可能なのか調べましょう。
因数分解により、高次式の値を計算する
なお、ここまでの知識は高次式の計算にも役立ちます。複雑な計算であっても、因数分解することによって計算を簡単にできるのです。
それでは、実際に練習問題を解いてみましょう。\(x=1+\sqrt{2}i\)のとき、以下の式の答えは何でしょうか。
- \(P(x)=x^4-4x^3+2x^2+8x-9\)
\(x=1+\sqrt{2}i\)を代入して計算する場合、複雑な計算となります。そこで、式の次数を下げることによって計算を簡略化しましょう。
次数を下げるため、\(x=1+\sqrt{2}i\)を利用して割る数を作ります。方針としては、根号と虚数単位\(i\)を消しましょう。以下のように計算します。
\(x=1+\sqrt{2}i\)
\(x-1=\sqrt{2}i\)
\((x-1)^2=2i^2\)
\(x^2-2x+1=-2\)
\(x^2-2x+3=0\)
こうして、\(x=1+\sqrt{2}i\)を\(x^2-2x+3=0\)へ変換することができました。次に、\(P(x)\)に対して\(x^2-2x+3\)で割るとき、商\(Q(x)\)と余り\(R\)を利用して表しましょう。
- \(P(x)=(x^2-2x+3)Q(x)+R\)
そこで、\(Q(x)\)と\(R\)を求めましょう。以下のように割り算によって計算します。
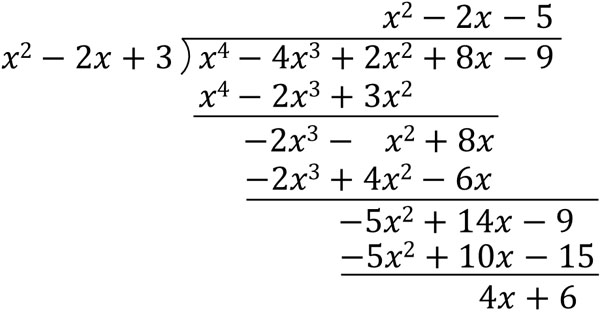
こうして、以下のように式を変形できます。
\(P(x)=(x^2-2x+3)(x^2-2x-5)\)\(+4x+6\)
前述の通り、\(x=1+\sqrt{2}i\)の場合、\(x^2-2x+3=0\)です。そのため、\((x^2-2x+3)(x^2-2x-5)=0\)です。つまり、あなたが計算すればいいのは余りの部分だけです。
\(P(1+\sqrt{2}i)=0+4(1+\sqrt{2}i)+6\)
\(=10+4\sqrt{2}i\)
こうして、答えは\(10+4\sqrt{2}i\)とわかりました。次数を下げずに計算すると、計算過程が複雑です。そこで剰余の定理を利用して、次数を下げることで計算を簡略化しましょう。
・複素数であっても恒等式は成り立つ
なお、先ほどの計算では複素数を用いました。恒等式は実数だけでなく、複素数であっても成り立ちます。そのため虚数を含む式であっても、恒等式に複素数を代入することで計算しましょう。
剰余の定理と因数定理を使いこなす
新たな公式を覚える必要はないものの、理解するべき内容に剰余の定理があります。割る数について、商と余りを利用して式を作るのです。これにより、割り算をしなくても余りの数を得ることができます。
公式を覚えても剰余の定理を利用できるようになることはありません。そこで、剰余の定理が何を意味しているのか学びましょう。
なお、剰余の定理で余りが0になる場合、因数定理を利用できます。余りが0であれば、その一次式は因数となります。そのため高次式の因数分解をする場合、因数定理が役に立ちます。
一次式と商、余りの関係を利用する定理が剰余の定理と因数定理です。これらの定理が何を意味しているのか学び、定理を利用することで問題を解けるようになりましょう。