通常、光(電磁波)が物体に当たっても波長が変化することはありません。ただ電磁波の中でも、X線を物体に当てて散乱させると、波長が長くなることが知られています。これをコンプトン効果(コンプトン散乱)といいます。
なぜコンプトン散乱が起こるのかを説明するとき、光量子仮説が利用されます。つまり、光は波だけでなく、粒子としての性質をもつというわけです。
コンプトン効果が起こることを理解するためには、光が粒子であることを利用して、運動量保存則を利用することになります。そのため、公式を利用することによって粒子の運動量を計算しましょう。また、エネルギー保存則を利用しての計算も必要になります。
それでは、X線の散乱ではどのように波長が変化するのでしょうか。公式を利用することにより、粒子の運動量を計算する方法を解説していきます。
もくじ
光量子仮説を実験で証明したコンプトン効果
アインシュタインが光量子仮説を提唱し、光は波だけでなく、粒子としての性質をもつことが説明されました。光量子仮説により、光電効果を説明することができます。
なお、光が粒子であるのであれば、光は運動量をもつとアインシュタインは考えました。この考えを証明した実験がコンプトン散乱です。
通常、波が反射するとき、波長や振幅、速さが変化することはありません。固定端反射によって位相が変化することはあるものの、その他の要素に変化はないのです。ただ光の中でも、X線については、物体に当たって散乱すると散乱前よりも波長が長くなります。
そこで、物理学者であるコンプトンは次のように考えました。
- 光(電磁波)は粒子としての性質をもつ。X線も電磁波であるため、粒子としての性質をもつはずだ。
そこで、彼はX線の光子が粒子としてふるまうことを利用してコンプトン散乱を説明したわけです。
コンプトン効果の理論
それでは、どのように考えてコンプトンはコンプトン効果の説明をしたのでしょうか。公式を利用して運動量保存やエネルギー保存の計算をする前に、彼が考えた理論を確認しましょう。
「X線によって起こる散乱というのは、X線光子と物体が衝突することによって起こる」とコンプトンは考えました。X線光子はエネルギーをもつため、X線光子と物体が衝突することによって、エネルギーの一部が物体に移動します。
アインシュタインが提唱した光量子仮説では、光子がもつエネルギー\(E\)は以下の公式によって計算できます。
- \(E=hν=h\displaystyle\frac{c}{λ}\)
公式を確認してわかる通り、電磁波(X線)のエネルギー\(E\)が減少する場合、波長\(λ\)は長くなる必要があります。これが、コンプトン効果によってX線の波長が長くなる理由です。
光子の運動量を得る公式
それでは、散乱によってX線の波長がどれくらい長くなるのか計算しましょう。実験結果と計算結果が合致する場合、理論が正しいと証明されることになります。
力学で物体が衝突するとき、利用されるのが運動量保存の法則です。アインシュタインは粒子の運動量についても述べています。プランク定数を\(h\)、光の速さを\(c\)とするとき、振動数\(ν\)、波長\(λ\)の光子がもつ運動量\(p\)は以下になります。
- \(p=\displaystyle\frac{hν}{c}=\displaystyle\frac{h}{λ}\)
なお物理では、単位を一致させることが重要です。力学では、速さ\(v\)、質量\(m\)の物体がもつ運動エネルギーは\(\displaystyle\frac{1}{2}mv^2\)[J]です。また光子のエネルギーは\(E=hν\)であり、単位は同様にJ(ジュール)です。
一方、運動量は\(mv\)であるため、\(\displaystyle\frac{1}{2}mv^2\)[J]に対して\(v\)[m/s]で割ることによって運動量の単位を得ることができます。同様に\(hν\)[J]に対して光速\(c\)[m/s]で割ることにより、単位を合わせることができます。
また波で学んだ公式である\(v=fλ\)より、\(c=νλ\)です。そのため、\(ν=\displaystyle\frac{c}{λ}\)です。そこで\(ν=\displaystyle\frac{c}{λ}\)を\(p=\displaystyle\frac{hν}{c}\)へ代入することにより、\(p=\displaystyle\frac{h}{λ}\)を得ることができます。
\(x\)軸方向と\(y\)軸方向で運動量保存の式を作る
それでは、静止している質量\(m\)の電子に波長\(λ\)のX線が衝突する場面を考えましょう。散乱後のX線の角度は\(Φ\)であり、波長は\(λ’\)へ変化するとします。また電子ははね返されることによって、角度θにて速さ\(v\)で動きます。
この場合、以下の図を作ることができます。
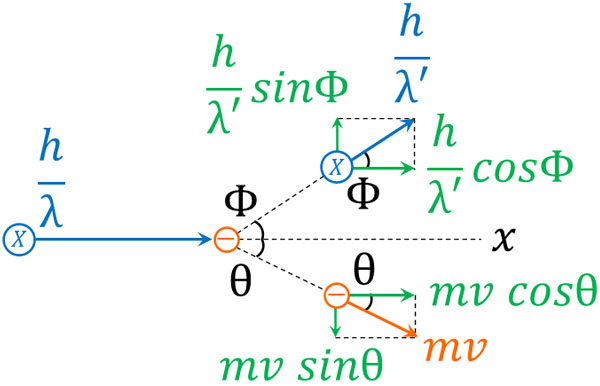
そこで、\(x\)軸方向と\(y\)軸方向で運動量保存の式を作りましょう。
- \(x\)軸方向:\(\displaystyle\frac{h}{λ}=\displaystyle\frac{h}{λ’}cosΦ+mv·cosθ\)
- \(y\)軸方向:\(\displaystyle\frac{h}{λ’}sinΦ=mv·sinθ\)
これらの式に加えて、エネルギー保存則を利用して式を作ります。通常、2つの物体が衝突するときは力学的エネルギー保存則を利用できません。衝突により、音や熱としてエネルギーが消費されるため、衝突の前後で運動エネルギーは一致しないのです。
しかし光子と電子の衝突では、弾性衝突によって音や熱などによるエネルギーの損失がないと仮定してエネルギー保存則を利用します。力学的エネルギー保存則を利用すると、以下の式を作れます。
- \(\displaystyle\frac{hc}{λ}=\displaystyle\frac{hc}{λ’}+\displaystyle\frac{1}{2}mv^2\)
こうして、合計で3つの式を作ることができました。
運動量保存則とエネルギー保存則を利用して公式を導出する
それでは先ほどの式を利用して、コンプトン効果が起こった後の波長の長さを計算しましょう。\(sin^2θ+cos^2θ=1\)であるため、以下の式をつくれます。
\((mg)^2·sin^2θ+(mg)^2·cos^2θ=(mg)^2\)
\((mg·sinθ)^2+(mg·cosθ)^2=(mg)^2\)
先ほどの計算より、\(\displaystyle\frac{h}{λ}=\displaystyle\frac{h}{λ’}cosΦ+mv·cosθ\)、\(\displaystyle\frac{h}{λ’}sinΦ=mv·sinθ\)であるため、以下のように計算しましょう。
\((mg)^2=(mg·sinθ)^2+(mg·cosθ)^2\)
\((mg)^2=\left(\displaystyle\frac{h}{λ’}sinΦ\right)^2+\left(\displaystyle\frac{h}{λ}-\displaystyle\frac{h}{λ’}cosΦ\right)^2\)
\((mg)^2=\displaystyle\frac{h^2}{λ’^2}sin^2Φ+\displaystyle\frac{h^2}{λ^2}\)\(-\displaystyle\frac{2h^2}{λλ’}cosΦ\)\(+\displaystyle\frac{h^2}{λ’^2}cos^2Φ\)
\((mg)^2=\displaystyle\frac{h^2}{λ’^2}(sin^2Φ+cos^2Φ)+\displaystyle\frac{h^2}{λ^2}\)\(-\displaystyle\frac{2h^2}{λλ’}cosΦ\)
\((mg)^2=\displaystyle\frac{h^2}{λ’^2}+\displaystyle\frac{h^2}{λ^2}\)\(-\displaystyle\frac{2h^2}{λλ’}cosΦ\)
\((mg)^2=h^2\left(\displaystyle\frac{1}{λ^2}+\displaystyle\frac{1}{λ’}-\displaystyle\frac{2}{λλ’}cosΦ\right)\) – ①
次に、力学的エネルギー保存則を利用して得た式を以下のように変形しましょう。
\(\displaystyle\frac{hc}{λ}=\displaystyle\frac{hc}{λ’}+\displaystyle\frac{1}{2}mv^2\)
\(\displaystyle\frac{hc}{λ}-\displaystyle\frac{hc}{λ’}=\displaystyle\frac{1}{2}mv^2\)
\((mv)^2=\displaystyle\frac{2mhc}{λ}-\displaystyle\frac{2mhc}{λ’}\)
\((mv)^2=2mhc\left(\displaystyle\frac{1}{λ}-\displaystyle\frac{1}{λ’}\right)\) – ②
①と②を利用することにより、以下の計算をすることができます。
\(2mhc\left(\displaystyle\frac{1}{λ}-\displaystyle\frac{1}{λ’}\right)=\)\(h^2\left(\displaystyle\frac{1}{λ^2}+\displaystyle\frac{1}{λ’}-\displaystyle\frac{2}{λλ’}cosΦ\right)\)
\(2mhc\displaystyle\frac{λ’-λ}{λλ’}=\)\(h^2\left(\displaystyle\frac{λ’^2+λ^2}{λ^2λ’^2}-\displaystyle\frac{2}{λλ’}cosΦ\right)\)
この式に対して、両辺に\(λλ’\)をかけましょう。
\(2mhc(λ’-λ)=\)\(h^2\left(\displaystyle\frac{λ’^2+λ^2}{λλ’}-2cosΦ\right)\)
この式に対して、両辺を\(2mhc\)で割りましょう。
\(λ’-λ=\displaystyle\frac{h}{2mc}\left(\displaystyle\frac{λ’^2+λ^2}{λλ’}-2cosΦ\right)\)
なお\(λ’-λ\)というのは、コンプトン散乱によって生じる波長の変化\(Δλ\)を表します。そこで、以下のように式を変えましょう。
\(Δλ=\displaystyle\frac{h}{2mc}\left(\displaystyle\frac{λ’^2+λ^2}{λλ’}-2cosΦ\right)\)
また、\(λ’^2+λ^2\)は\((λ’-λ)^2+2λλ’\)へ変形できます。そこで、以下のように式を変えます。
\(Δλ=\displaystyle\frac{h}{2mc}\left(\displaystyle\frac{(λ’-λ)^2+2λλ’}{λλ’}-2cosΦ\right)\)
\(Δλ=\displaystyle\frac{h}{2mc}\left(\displaystyle\frac{(λ’-λ)^2}{λλ’}+2-2cosΦ\right)\)
なお\(Δλ=λ’-λ\)について、\(Δλ\)の値が非常に小さいのであれば、その二乗である\((λ’-λ)^2\)は限りなくゼロに近い値であり、無視することができます。そこで、\((λ’-λ)^2=0\)と考えましょう。そうすると、式は以下のようになります。
\(Δλ=\displaystyle\frac{h}{2mc}(2-2cosΦ)\)
\(Δλ=\displaystyle\frac{h}{mc}(1-cosΦ)\)
こうして、コンプトン効果の式である\(Δλ=\displaystyle\frac{h}{mc}(1-cosΦ)\)を得ることができました。公式を確認すると、X線が電子へ衝突することによって波長が長くなるとわかります。
コンプトン散乱を得る公式を覚えても意味がないため、運動量保存則と力学的エネルギー保存則を利用して、式を導き出せるようになりましょう。
X線を用いたコンプトン散乱の原理と光の粒子性を学ぶ
光は波であるものの、波では説明できない現象が存在します。その一つがコンプトン効果(コンプトン散乱)です。光を粒子と考えなければ、X線が電子に当たって散乱するとき、波長が変化する理由を説明できないのです。
光量子仮説では、光はエネルギーだけでなく、運動量をもつと考えます。X線を光子と考え、運動量保存則と力学的エネルギー保存則を利用することにより、衝突後の波長の変化を計算できます。
そこで、粒子に関する運動量の公式を利用できるようになりましょう。また、コンプトン効果の公式を導き出せるようになりましょう。
実験によって現象が確認されている場合、理論や数式によって説明できれば、物理では多くの人に受け入れられます。コンプトンは光量子仮説を利用することにより、数式と共にコンプトン効果を説明したのです。光電効果とは異なる方法で光の粒子性を説明できる現象がコンプトン効果です。






