原子を学ぶとき、重要な内容の一つがX線の発生です。電子を高速で陽極に衝突させることにより、X線を発生させることができるのです。
X線には連続X線と特性X線(固有X線)があります。そこで、X線がもつエネルギーを計算できるようになりましょう。
またX線には波としての性質があります。つまり、X線は干渉によって互いに強め合います。X線回折は別名でブラッグ反射と呼ばれています。ブラッグ反射を利用することにより、結晶構造の解析に役立ちます。
それでは、X線の性質や公式には何があるのでしょうか。X線のエネルギーの計算方法やブラッグ反射の式を含めて解説していきます。
もくじ
波長の短い電磁波がX線
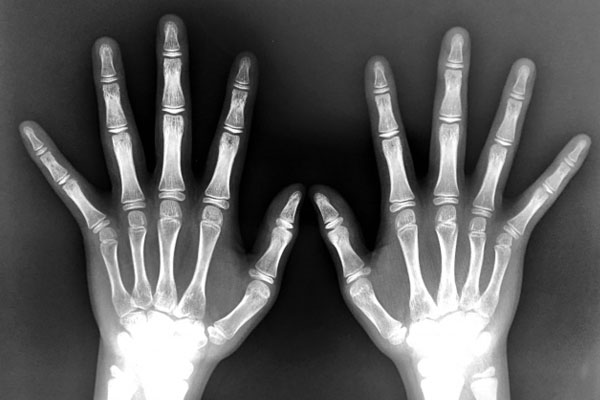
ノーベル物理学の最初の受賞者はドイツの物理学者であるレントゲンです。彼はX線を発見し、X線の利用は医療診断で欠かせない技術となっています。
X線は皮膚や筋肉を透過するものの、骨を透過しません。そのため、人体にメスを入れなくても体内の様子を観察できるのです。謎の放射線として発見されたため、X線と名付けられました。
X線は電磁波の一種であり、光(電磁波)は波長によってエネルギーが異なります。例えば可視光や赤外線、紫外線であれば、以下の波長になります。
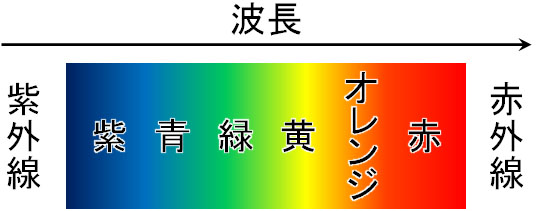
紫外線は日焼け(皮膚の炎症)を起こす原因になることからわかる通り、高いエネルギーをもっているとわかります。つまり、波長の短い波であるほどエネルギーが高いです。
X線は紫外線よりも短い波長の波です。また波長\(λ\)が短いというのは、振動数\(ν\)が大きいことを意味しています。また振動数\(ν\)が大きいと、その分だけエネルギー\(E\)も高くなります。
| X線 | 紫外線 | 赤外線 | |
| 波長\(λ\) | 短い | 短い | 長い |
| 振動数\(ν\) | 大 | 大 | 小 |
| エネルギー\(E\) | 大 | 大 | 小 |
なお、紫外線よりもX線のほうが波長は短く、振動数とエネルギーは大きいです。X線は放射線の一種であるため、紫外線よりも高いエネルギーをもつのは容易に理解できます。
X線のスペクトルと公式:連続X線と特性X線(固有X線)
それでは、どのようにX線を発生させるのでしょうか。陰極線(電子の集まり)に対して高い電圧を加えると、電子は加速します。「加速した電子を陽極(金属)と衝突させると、X線を生じる」という事実をレントゲンは発見しました。
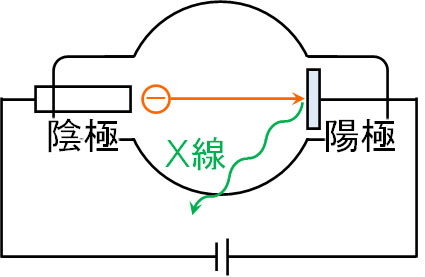
このとき発生するX線にはさまざまな波長が含まれます。可視光にさまざまな波長の光が含まれているのと同じように、多くの種類の波長をもつX線が発生するのです。そこで、発生するX線の波長と強度をグラフにしましょう。
X線の波長とX線の強度の関係をスペクトルといいます。X線のスペクトルは以下のようになります。
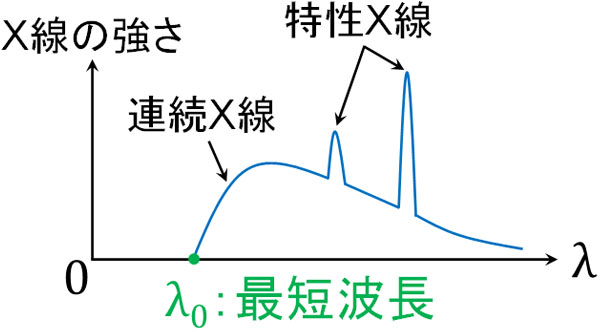
X線の強度(強さ)というのは、X線の明るさと考えましょう。X線光子で考える場合、X線光子の数がX線の強度に該当します。特定の波長について、どれだけの明るさ(X線光子の数)を得られたのかをX線の強度は表しているのです。
このとき、グラフで滑らかな曲線部分を連続X線といいます。それに対して、グラフで鋭いピークとなっている部分を特性X線(または固有X線)といいます。
なお、グラフで最も短い波長\(λ_0\)を最短波長といいます。光子がもつエネルギーは\(E=h\displaystyle\frac{c}{λ}\)で表すことができます。そのため最短波長\(λ_0\)というのは、最もエネルギーが高いX線であるとわかります。
最短波長では、電子がもつ運動エネルギーをすべて受け取り、X線のエネルギーに変換されることになります。そのためエネルギー保存則が成り立ちます。電子の電気量は\(e\)であり、電圧を\(V\)とすると、エネルギーは\(eV\)です。そのため、以下の式を作ることができます。
- \(eV=h\displaystyle\frac{c}{λ_0}\)
また、この式を以下のように変形すると最短波長\(λ_0\)を計算できます。
- \(λ_0=\displaystyle\frac{hc}{eV}\)
それでは、最短波長で「すべての運動エネルギーがX線のエネルギーへと変換される」と考えるのはなぜなのでしょうか。また、連続X線や特性X線を生じるとき、どのような現象が起こっているのでしょうか。これらをより詳しく確認しましょう。
連続X線と特性X線の発生の仕組み
まず、連続X線を生じるときに起こる現象を説明します。電子が金属内を通過するとき、電子が原子と衝突することなく、電子の進路が曲がる場合、電子はエネルギーの一部を失います。言い換えると、電子のスピードが遅くなることによって運動エネルギーが失われ、失われたエネルギーはX線として放射されます。
この現象によって発生するX線が連続X線です。電子がもつ運動エネルギーの減少分がX線のエネルギーになるため、金属内での電子の速さ(電子の進路が曲げられた後の速さ)が\(v’\)の場合、X線光子がもつエネルギー\(E=hν\)との関係は以下のようになります。
- \(\displaystyle\frac{1}{2}mv^2-\displaystyle\frac{1}{2}mv’^2=hν\)
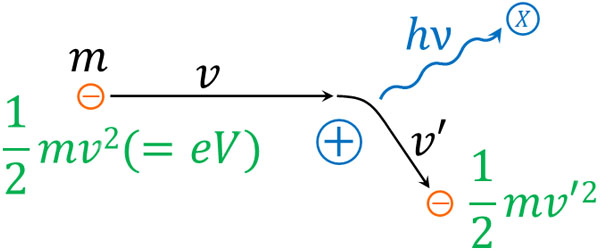
なお最短波長\(λ_0\)では、エネルギー\(E=hν=h\displaystyle\frac{c}{λ_0}\)が最大になります。言い換えると、\(\displaystyle\frac{1}{2}mv’^2\)がゼロになります。そのため、\(eV=h\displaystyle\frac{c}{λ_0}\)が成り立つのです。
・特性X線の発生の仕組み
それでは、特性X線はどのようにして発生するのでしょうか。陰極から発せられた電子のすべてが曲がるわけではなく、一部は陽極原子と衝突します。このとき電子によって、原子が保有している電子を弾き飛ばします。
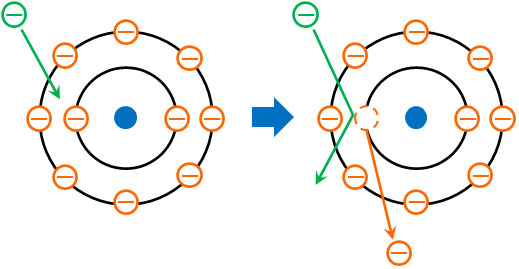
電子は内側の電子殻から順に格納されます。陽子はプラスの電荷をもち、電子はマイナスの電荷をもつため、互いに近くにあるほうがエネルギーは低くなり、安定します。
ただ高速の電子によって、電子殻の内側に存在する電子が弾き飛ばされる場合、原子は不安定になります。この場合、電子殻の外側に存在していた電子が電子殻の内側へ移動します。つまり、電子は不安定な場所(外側の電子殻)から安定な場所(内側の電子殻)へと移動します。
電子が内側の電子殻へ移動するためには、余分なエネルギーを放出しなければいけません。このとき、X線として電子はエネルギーを放出します。
特性X線の強さというのは、電子殻のエネルギー差によって生まれます。外側の電子殻と内側の電子殻でエネルギーに差があるほど、特性X線のエネルギーは大きくなります。
連続X線と特性X線(固有X線)では、X線が発生する仕組みがまったく異なります。そのため、連続X線と特性X線を分けて考えなければいけません。
電子の加速電圧とX線グラフの関係
先ほど記したX線のスペクトルについて、加える電圧を高くすることにより、電子のスピードを上げる場合はどのようなグラフになるのでしょうか。電子の加速電圧とX線グラフの関係を確認しましょう。
例えば電圧を上げて電子のスピードを上げるとグラフは以下のように変化します。
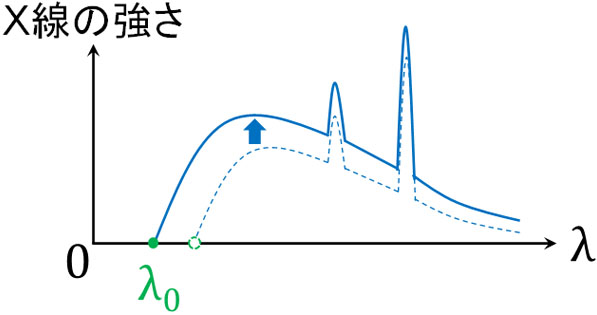
このようにX線の強さが大きくなり、最短波長\(λ_0\)が短くなります。ただ、特性X線を発する波長は変化しません。
電圧を大きくすると、エネルギー\(eV\)が大きくなるため、その分だけ電子の運動エネルギーが高くなることでX線の強さは大きくなります。また先ほど解説した通り\(eV=h\displaystyle\frac{c}{λ_0}\)が成り立つため、電圧を上げると最短波長\(λ_0\)の値は小さくなります。
一方、特性X線は電子殻のエネルギー差によって生まれるため、特性X線の波長に変化はありません。あくまでも、X線の強さが大きくなるだけです。
X線の波動性:X線の回折と干渉
なおX線は電磁波の一種であるため、可視光と同様に波としての性質をもちます。波である場合、回折したり、ほかの波と干渉したりします。そこで、X線の回折と干渉について確認しましょう。
波の干渉で重要な実験としてヤングの実験が知られています。スリットを利用することにより、明暗の線を作る実験がヤングの実験です。
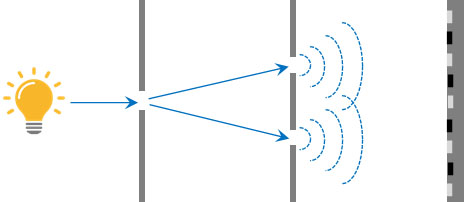
ただX線の波長は非常に短く、可視光に比べて波長の長さは1000分の1ほどです。そのためX線の波長に比べてスリット幅が非常に大きく、スリットを利用しても回折・干渉現象を観察することはできません。
そこで食塩の結晶など、特定の物質によって構成されている結晶を利用しましょう。結晶を利用すれば、X線による回折・干渉が起こることが知られています。結晶内の原子の間隔はX線の波長とほぼ同じであるため、結晶であればX線を散乱させることができるのです。
結晶によって表れる、X線による回折・干渉の像をラウエ斑点といいます。規則的に原子が並ぶことによって結晶となっており、結晶にX線が当たることで散乱し、干渉を起こすのです。実際にこの現象をスクリーンに映すと、以下のようになります。
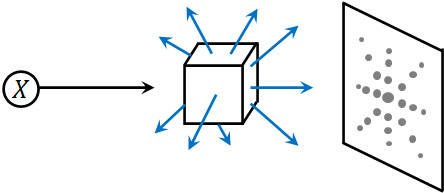
干渉によってラウエ斑点を得ることができるため、X線には波動性があると証明されています。
X線が強め合う条件:ブラッグ反射の条件(ブラッグの式)
干渉が起こるとき、散乱した波が強め合うことになります。それでは、どのような条件でX線が強め合うのでしょうか。
結晶では原子が規則正しく並んでいます。原子にX線が当たると、X線は散乱します。このとき結晶の間隔を\(d\)、X線と結晶面との角度を\(θ\)とすると、以下の図を作ることができます。
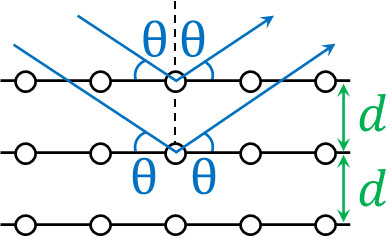
波が強め合う条件を得るためには、経路差を計算しなければいけません。そこで以下の図を作ると、経路差は\(2dsinθ\)であるとわかります。
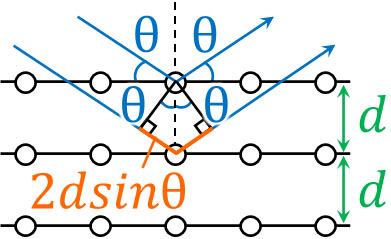
なお位相が同じ場合、半波長\(\displaystyle\frac{λ}{2}\)の偶数倍であれば、波は強め合うことになります。そのため以下の条件のとき、X線は干渉によって強め合います。
- \(2dsinθ=\displaystyle\frac{λ}{2}×2m\)(\(m=0,1,2…\))
この条件をブラッグ反射の条件(ブラッグの式)といいます。X線回折を用いた結晶構造の解析では、ブラッグの式は非常に重要です。
原子間隔がわかっている場合、ブラッグの式を利用することによってX線の波長がわかります。またX線の波長がわかっている場合、結晶の原子間隔を測定できます。そのため、ブラッグ反射の条件は結晶構造の解析でひんぱんに利用されるのです。
なおここまで、光量子仮説を用いてX線のエネルギーを解説してきました。また、ブラッグ反射の条件を利用することによってX線の波動性を解説してきました。これはつまり、X線には粒子性と波動性が存在することを意味しています。
事実、コンプトン効果はX線を利用するときに起こります。そのため、X線には粒子性があります。いずれにしても、X線は他の光(電磁場)と同様に粒子性と波動性をもちます。
X線の特徴とX線回折・干渉の条件を知る
X線を利用することにより、医療診断で利用されるレントゲン写真を撮影できます。電子に対して高圧電圧をかけることによってX線を発生させることができるのです。
このとき、X線には連続X線と特性X線(固有X線)の2種類があります。連続X線と特性X線は発生メカニズムが異なります。そのため高い電圧をかけることで電子の速度を加速させるとき、最短波長は変化するものの、特性X線が表れる波長に変化はありません。
なおX線には波動性があり、結晶に当たることによって回折・干渉現象が起こります。波の強め合いが起こるときの式をブラッグの式といいます。ブラッグ反射の条件は結晶構造解析で重要であり、原子間隔を測定できます。
X線の粒子性と波動性を利用することにより、X線が関わる物理現象を説明できます。粒子性と波動性の両方を学び、これらの現象を理解しましょう。






