コンデンサーでの電気量保存の法則とキルヒホッフの法則の利用

電荷を蓄積しているコンデンサーを含む回路を利用して、計算問題を解かなければいけないことは多いです。このとき、問題の解き方があります。

回路に複数のコンデンサーが存在する場合、電気量保存の法則を利用しましょう。コンデンサーによって独立している場所がある場合、電気量保存の法則により、電気量の総和は同じになります。

それに加えて、キルヒホッフの法則を利用しましょう。回路を一周する場合、電圧$V$はゼロになります。コンデンサーではオームの法則ではなく、公式として$Q=CV$を利用します。そこで、この公式とキルヒホッフの法則を利用して式を作りましょう。

それでは、具体的にどのようにして式を作り、答えを得ればいいのでしょうか。電荷を蓄積しているコンデンサーを含む回路について、電気量保存の法則とキルヒホッフの法則を利用する手順を解説していきます。

電荷を蓄積しているコンデンサーを含む回路の計算手順

電荷を蓄積しているコンデンサーを回路に含むケースは多く、このときの計算方法は決まっています。以下の2ステップによって電気量や電圧（電位差）を計算します。

• 電気量保存の法則を利用して式を作る
• キルヒホッフの第二法則を利用して式を作る

それぞれの詳細を確認していきましょう。

電気量保存の法則：コンデンサーの独立場所は電気量の総和が同じ

電気を学ぶとき、すべての人が電気量保存の法則を学びます。電気量保存の法則はコンデンサーにも当てはまります。つまり、電荷が勝手に生まれたり消えたりすることはないのです。具体的には、電荷を蓄積しているコンデンサーでは、回路で独立している部分は電気量の総和が同じになります。

充電により、コンデンサーに電荷が蓄積します。このときコンデンサーには電位差があります。電圧は電気的な高さであり、イメージとしては崖のようになっています。電荷は崖を自由に登ったり下りたりすることはできません。

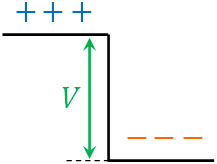
つまり、電荷の移動は必ず導線に沿って行われます。

それでは、以下のように10Cの電荷が蓄積しているコンデンサー$C_1$と4Cの電荷が蓄積しているコンデンサー$C_2$を考えてみましょう。

この場合、回路内で独立している部分（導線がつながっていない部分）の電気量の総和は常に同じです。具体的には、以下の部分を足すと合計は-6Cです。

$-10+4=-6$

それでは、スイッチを入れることにより、下図のように$C_1$の電気量が12Cになった場合、$C_2$の電気量はどのように変化するでしょうか。

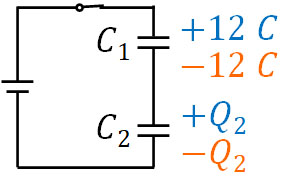
電気量保存の法則より、独立している部分の電気量の合計は-6Cです。そのため、以下の式を作ることができます。

$-12+Q_2=-6$

$Q_2=6$

こうして、$C_2$の電気量は6Cと計算できます。電気量の計算をするとき、電気量保存の法則を利用しましょう。

キルヒホッフの法則を利用して式を作る

なお回路にコンデンサーが存在する場合、キルヒホッフの第二法則を利用することによって式を作りましょう。回路を一周する場合、電位差がゼロになる法則がキルヒホッフの第二法則です。

なお、コンデンサーは2枚の金属板によって構成されています。そのため電源とは異なり、正極と負極が明確に決まっていません。回路の構造によって正極板になったり、負極板になったりします。そこで、キルヒホッフの法則を利用する前にマークを書き加えることによって正極板と負極板を区別しましょう。

例えば以下のように、電源の起電力が$V$、コンデンサーの電位差がそれぞれ$V_1$、$V_2$となっている回路を考えてみましょう。

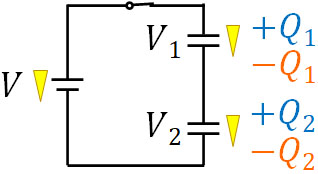
どのようなマークを利用しても問題ないですが、電位の低いほうから高いほうへ登っていくイメージにより、三角形を利用するとわかりやすいです。上図の場合、三角形でとがっている部分が低電位、三角形の底が高電位です。

この場合、キルヒホッフの法則より以下の式を作ることができます。

$V+(-V_1)+(-V_2)=0$

なおコンデンサーの公式より、$Q=CV$であるため、$V=\displaystyle\frac{Q}{C}$です。そこで、$V=\displaystyle\frac{Q}{C}$を利用して先ほどの式に代入し、計算しましょう。

電荷の蓄積に関するコンデンサーの練習問題

それでは、実際に練習問題を解いてみましょう。練習問題を解くことにより、コンデンサーで起こる現象を理解できるようになります。

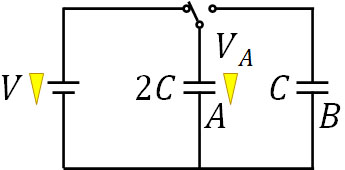
電圧$V$の電池、電気容量$2C$のコンデンサーA、電気容量$C$のコンデンサーBが下図のように配置されています。最初、AとBに電荷は存在しません。

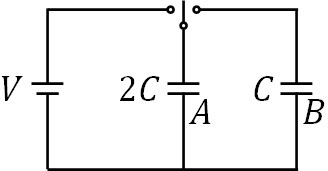
1. スイッチを左に一回入れる場合、コンデンサーAに蓄積される電気量$Q_A$はいくらですか。
2. (1)の操作後、スイッチを右に一回入れる場合、コンデンサーBに蓄積される電気量$Q_B$はいくらですか。
3. (2)の操作後、スイッチを左に一回、次に右に一回入れる場合、AとBに蓄積される電気量はそれぞれいくらですか。
4. (1)と(2)の操作を無限回行う場合、コンデンサーAとコンデンサーBの電位差はいくらになりますか。

電気量保存の法則とキルヒホッフの法則を利用して問題を解きましょう。

キルヒホッフの法則を利用し、電荷量を計算する

1) スイッチを左に一回入れる場合、コンデンサーAに蓄積される電気量$Q_A$はいくらですか

まず、電圧を計算しましょう。コンデンサーAの電圧を$V_A$とすると、以下のようになります。

$V+(-V_A)=0$

$V_A=V$

なお、電源（電池）に直接つながっているため、キルヒホッフの法則を利用しなくても、$V_A=V$とわかります。またコンデンサーの公式より、$Q_A=2CV$と計算できます。そのため、コンデンサーAの電気量は$Q_A=2CV$です。

電気量保存の法則とキルヒホッフの法則とを利用する

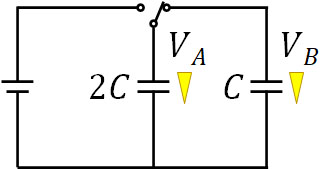
2) (1)の操作後、スイッチを右に一回入れる場合、コンデンサーBに蓄積される電気量$Q_B$はいくらですか

(1)の操作をすることにより、電荷を蓄積しているコンデンサーを作ることができました。次に、スイッチを右に入れます。この場合、導線は電源（電池）につながっておらず、独立しています。そこで、電気量保存の法則を利用して式を作りましょう。

なお、スイッチを右に入れた後の電気量をそれぞれ$Q_A’$、$Q_B’$とします。電気量保存の法則より、以下の計算をしましょう。

$Q_A=Q_A’+Q_B’$

$2CV=Q_A’+Q_B’$

また前述の通り、$Q=CV$であるため、$V=\displaystyle\frac{Q}{C}$です。そのためキルヒホッフの法則より、以下の式を作れます。

$V_A+(-V_B)=0$

$\displaystyle\frac{Q_A’}{2C}-\displaystyle\frac{Q_B’}{C}=0$

$Q_A’-2Q_B’=0$

$Q_A’=2Q_B’$

そこで、$Q_A’=2Q_B’$を$2CV=Q_A’+Q_B’$に代入しましょう。

$2CV=Q_A’+Q_B’$

$2CV=2Q_B’+Q_B’$

$Q_B’=\displaystyle\frac{2}{3}CV$

こうして、$Q_B’=\displaystyle\frac{2}{3}CV$と計算できました。また$Q_B’=\displaystyle\frac{2}{3}CV$であるため、$Q_A’=\displaystyle\frac{4}{3}CV$です。

同じ操作を繰り返す場合の計算方法

3) (2)の操作後、スイッチを左に一回、次に右に一回入れる場合、AとBに蓄積される電気量はそれぞれいくらですか

それでは、先ほどの操作を再び行う場合はどのようになるのでしょうか。スイッチを左に一回入れる場合、コンデンサーAの電位差は$V$となるため、電気量は再び$Q_A=2CV$となります。

その後、スイッチを右に入れます。先ほどの違いとしては、コンデンサーBは既に電気量として$\displaystyle\frac{2}{3}CV$が蓄積されています。また、電位差もあります。そこで、同様に電気量保存の法則とキルヒホッフの法則を利用して式を作りましょう。

・電気量保存の法則より

$2CV+\displaystyle\frac{2}{3}CV=Q_A’+Q_B’$

$\displaystyle\frac{8}{3}CV=Q_A’+Q_B’$

なおキルヒホッフの法則より、$V_A+(-V_B)=0$であるため、$Q_A’=2Q_B’$になると先ほど計算しました。そこで、$Q_A’=2Q_B’$を$\displaystyle\frac{8}{3}CV=Q_A’+Q_B’$に代入しましょう。

$\displaystyle\frac{8}{3}CV=Q_A’+Q_B’$

$\displaystyle\frac{8}{3}CV=2Q_B’+Q_B’$

$Q_B’=\displaystyle\frac{8}{9}CV$

こうして、$Q_B’=\displaystyle\frac{8}{9}CV$とわかりました。また$Q_B’=\displaystyle\frac{8}{9}CV$であるため、$Q_A’=\displaystyle\frac{16}{9}CV$です。

無限回、操作を行う場合はスイッチが存在しない状態と同じ

4) (1)と(2)の操作を無限回行う場合、コンデンサーAとコンデンサーBの電位差はいくらになりますか

スイッチを左に入れ、その後にスイッチを右に入れる操作を無限回行う場合、どのように考えればいいのでしょうか。仮に、1秒間に百万回の速さでスイッチを切り返る場合、実質的に下図のように導線がつながっている状態と考えることができます。

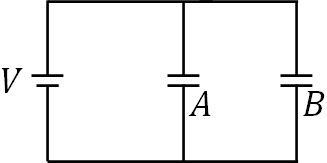
電源の起電力が$V$であり、コンデンサーが並列に存在しているため、計算しなくてもコンデンサーAとコンデンサーBの電位差（答え）はそれぞれ$V$とわかります。

それでは、計算によっても証明してみましょう。無限回、スイッチを切り替えるので、スイッチが左にある場合とスイッチが右にある場合では、コンデンサーBに蓄積されている電気量に変化はありません。理由としては、完全に充電されているからです。つまり、スイッチの切り替え前後でコンデンサーBに存在する電気量はいずれの場合も$Q_B$です。

またスイッチを左に入れ、電源と接続することにより、コンデンサーAの電位差は$V$となります。そのため、電気量保存の法則を利用して以下の式を作れます。

$2CV+Q_B=Q_A’+Q_B$

$Q_A’=2CV$

また前述の通り、キルヒホッフの法則より$Q_A’=2Q_B’$です。そのため、以下のように計算できます。

$Q_A’=2Q_B’$

$2CV=2Q_B’$

$Q_B’=CV$

コンデンサーBの電気容量は$C$であるため、$Q_B’=CV$の場合、電位差は$V$です。同様に考えると、コンデンサーAの電位差は$V$です。こうして、コンデンサーAとコンデンサーBの電位差（電圧）は両方とも$V$であると計算できました。

電荷の蓄積があるコンデンサーの計算方法は決まっている

物理では計算方法が決まっているケースがよくあります。その一つが「電荷の蓄積のあるコンデンサー」を含む回路です。

電荷の蓄積がある場合、回路内で独立している部分に着目しましょう。この場合、電気量保存の法則が成り立ちます。電気量保存の法則では、電気量の総和が必ず等しくなります。

また回路では、一周することによって必ず電位差がゼロになります。これをキルヒホッフの第二法則といいます。そこでキルヒホッフの第二法則を利用して、電位差の合計がゼロになるように式を作りましょう。

その後、2つの式を利用することによってコンデンサーに蓄積している電気量の計算が可能になります。計算方法を理解し、問題を解けるようになりましょう。