波の干渉条件で重要な内容の一つにくさび形空気層があります。2枚のガラスを利用することにより、明暗の線を作ることができるのです。

くさび形空気層の問題を解くとき、解き方を知っていれば正解を得ることができます。一方、公式を暗記して解き方を理解していない場合、正解を得ることはできません。公式を覚えても意味がないのは、波の干渉条件に共通しています。

くさび形空気層では、経路差の計算は非常に簡単です。ただ角度を利用して計算したり、屈折率の違いによる反射を考慮したりしなければいけません。

それでは、どのようにくさび形空気層の問題を解けばいいのでしょうか。公式の意味や経路差の計算方法、波の干渉条件を解説していきます。

くさび形空気層では、2枚のガラスで明線と暗線が作られる

まず、くさび形空気層の構造を学びましょう。2枚のガラスを利用し、紙など非常に薄い物体を利用することで生じるすき間をくさび形空気層といいます。

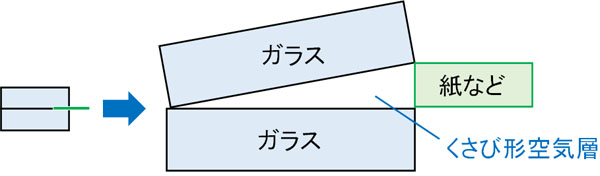
2枚のガラスを利用してすき間を作り、真上から見ると、明暗の縞模様が表れます。以下のような模様になります。

波の干渉によって明暗の線が表れます。光は波の一種であるため、干渉によって縞模様が観察されるのです。そこで、どのように明線と暗線が作られるのか計算できるようにしましょう。

光路差は空気層の幅の2倍：tanθを用いて経路差を表す

波が強め合う（または弱め合う）ためには、2つの波が必要になります。くさび形空気層では、波の干渉が起こるときは以下の部分で反射する2つの光を考えましょう。

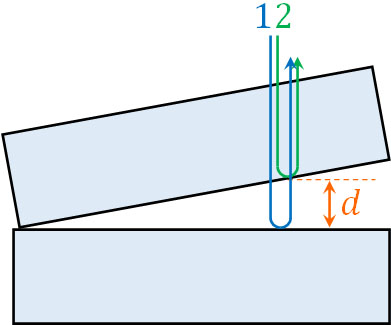
2つの光の距離の差（光路差）を計算すれば、波の干渉条件を得ることができます。くさび形空気層のすき間が\(d\)の場合、2倍した値（\(2d\)）が光路差であるとわかります。そのため、非常に簡単に2つの光の経路差（光路差）を計算できます。

ヤングの実験や回折格子の実験のように、面倒な計算をしなくても光路差を得られるのがくさび形空気層です。

・tanθを利用して経路差を出す

なお実際にくさび形空気層の計算問題を解くとき、角度を利用しなければいけない場面が存在します。以下の図について、角度θを利用して\(d\)を変形しましょう。

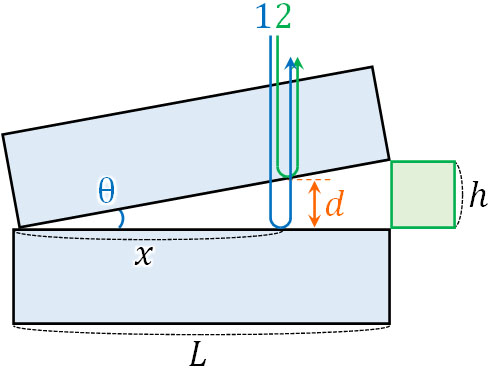
図より、tanθは以下のようになります。

  • \(tanθ=\displaystyle\frac{d}{x}=\displaystyle\frac{h}{L}\)

そのため、\(d=\displaystyle\frac{xh}{L}\)になります。つまり、2つの光の光路差を\(\displaystyle\frac{2xh}{L}\)と表記することもできます。

屈折率による反射の違い：自由端反射と固定端反射による位相

くさび形空気層を学ぶとき、屈折率による反射の違いを理解しなければいけません。反射には自由端反射と固定端反射が存在するため、反射の種類によって位相が変化するのです。

空気（真空）では屈折率が1です。一方、ガラスは空気よりも屈折率が高いです。つまり、ガラスは空気中（真空中）よりも光が進みにくく、波が伝わりにくいです。

そのため光が空気からガラスへ進むとき、固定端反射となります。反射するとき、屈折率の大きい媒質が固定された壁のように機能するのです。こうして固定端反射をする場合、波の位相は逆転します。

一方でガラスから空気へ進むときに反射する場合、空気は屈折率が低く、波は振動しやすいです。そのため自由端反射となり、位相の逆転は起こりません。

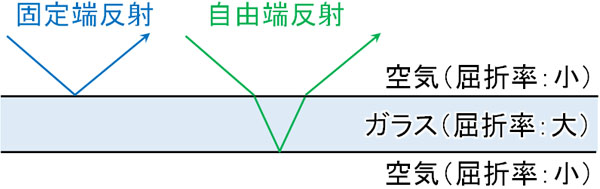そこでくさび形空気層について、反射の種類を確認しましょう。2つの光を確認すると、一方は自由端反射であり、一方は固定端反射であるとわかります。つまり、反射によって2つの光は逆位相になります。

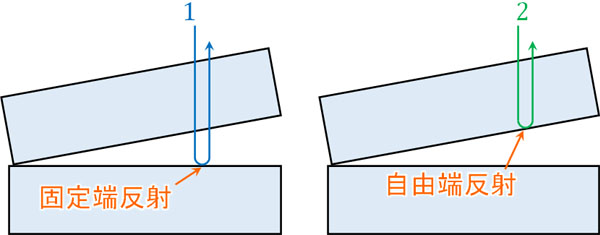
2つの光が逆位相になるため、半波長の奇数倍であれば強め合い、半波長の偶数倍であれば弱め合うとわかります。

波が強め合う条件と弱め合う条件

ここまでの内容を理解すれば、明線と暗線の干渉条件を出せます。2つの光の経路差は\(2d\)や\(\displaystyle\frac{2xh}{L}\)であるため、以下のようになります。

【強め合う条件（明線の条件）】

  • \(2d=\displaystyle\frac{λ}{2}×(2m+1)\) （\(m=0,1,2…\)）
  • \(\displaystyle\frac{2xh}{L}=\displaystyle\frac{λ}{2}×(2m+1)\) （\(m=0,1,2…\)）

【弱め合う条件（暗線の条件）】

  • \(2d=\displaystyle\frac{λ}{2}×2m\) （\(m=0,1,2…\)）
  • \(\displaystyle\frac{2xh}{L}=\displaystyle\frac{λ}{2}×2m\) （\(m=0,1,2…\)）

    こうして、明線と暗線の条件を得ることができました。

    明線（または暗線）の間隔を計算する

    次に、明線（または暗線）の間隔を計算しましょう。前述の通り、明線の条件は以下になります。

    • \(\displaystyle\frac{2xh}{L}=\displaystyle\frac{λ}{2}×(2m+1)\) （\(m=0,1,2…\)）

    そこで、以下のように式を変形しましょう。

    • \(x=\displaystyle\frac{λL(2m+1)}{4h}\)

    次に、\(m\)番目と\(m+1\)番目の線について間隔を計算しましょう。以下のようになります。

    \(Δx=\displaystyle\frac{λL(2m+3)}{4h}\)\(-\displaystyle\frac{λL(2m+1)}{4h}\)

    \(Δx=\displaystyle\frac{λL}{2h}\)

    こうして、明線の間隔は\(\displaystyle\frac{λL}{2h}\) とわかります。なお暗線の間隔も同じ値になるため、暗線の間隔も\(\displaystyle\frac{λL}{2h}\) です。

    スクリーンをガラスの下に置く場合の位相の変化

    ここまで、真上からくさび形空気層を見る場合について確認しました。それではスクリーンをガラスの下に置き、真下からくさび形空気層を確認する場合はどのようになるのでしょうか。2つの光の経路差は\(2d\)で共通しています。

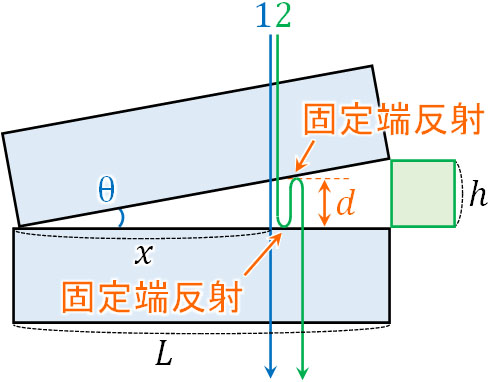
    なお一つの光は真下に透過するため、位相の変化はありません。またもう一方の光を確認すると、2ヵ所で固定端反射をしています。ガラスは空気中よりも屈折率が大きいため、波は振動しにくく、空気からガラスへ進むときに反射する場合は逆位相になるのです。

    2回の固定端反射をしているため、結果として2つの光は同位相になります。そのため、この場合の明線条件と暗線条件は以下のようになります。

    【強め合う条件（明線の条件）】

    • \(2d=\displaystyle\frac{λ}{2}×2m\) （\(m=0,1,2…\)）
    • \(\displaystyle\frac{2xh}{L}=\displaystyle\frac{λ}{2}×2m\) （\(m=0,1,2…\)）

    【弱め合う条件（暗線の条件）】

    • \(2d=\displaystyle\frac{λ}{2}×(2m+1)\) （\(m=0,1,2…\)）
    • \(\displaystyle\frac{2xh}{L}=\displaystyle\frac{λ}{2}×(2m+1)\) （\(m=0,1,2…\)）

    このように、真上から確認する場合に対して、真下から確認すると明線条件と暗線条件が反対になります。

    くさび形空気層に関する練習問題

    それでは、くさび形空気層に関する練習問題を解きましょう。以下の問題の答えは何でしょうか。

    • 以下の図について、上のガラスを固定し、下のガラスをゆっくりと下に移動させました。真上から確認するとき、明線に変化が表れました。

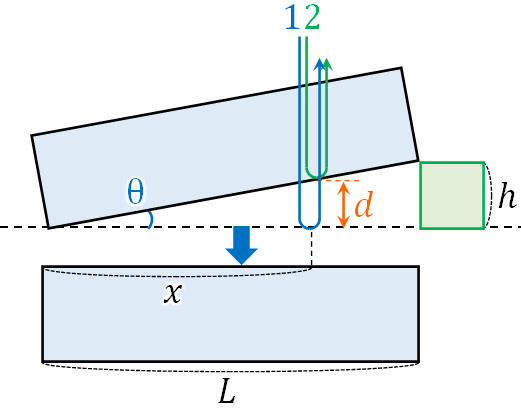
    1. 下のガラスを動かす前に位置\(x\)に存在した明線は左右のどちらに移動しましたか。明線の移動距離も求めましょう。
    2. 明線の間隔\(Δx\)はどのように変化しますか。
    3. ガラスの移動による明線の移動距離が\(l\)のとき、ガラスの下降距離を求めましょう。

    1) 下のガラスを動かす前に位置\(x\)に存在した明線は左右のどちらに移動しましたか。明線の移動距離も求めましょう

    ガラスを下に移動させた距離を\(Δd\)とします。この場合、2つの光の経路差（光路差）は\(2(d+Δd)\)です。

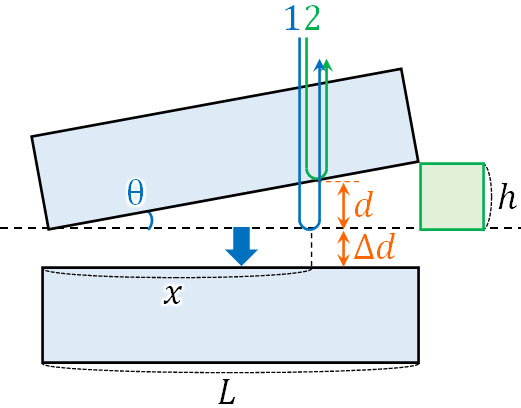
    また前に解説した通り、\(tanθ=\displaystyle\frac{d}{x}=\displaystyle\frac{h}{L}\)です。
    そのため、\(d=\displaystyle\frac{xh}{L}\)です。つまり、2つの光の光路差は以下のようになります。

    \(2(d+Δd)\)

    \(=2\left(\displaystyle\frac{xh}{L}+Δd\right)\)

    \(=\displaystyle\frac{2xh}{L}+2Δd\)

    そのため、明線の条件は以下になります。

    • \(\displaystyle\frac{2xh}{L}+2Δd\)\(=\displaystyle\frac{λ}{2}×(2m+1)\) （\(m=0,1,2…\)）

    そこで、位置\(x\)を確認しましょう。以下のようになります。

    \(\displaystyle\frac{2xh}{L}+2Δd=\displaystyle\frac{λ}{2}×(2m+1)\)

    \(\displaystyle\frac{2xh}{L}=\displaystyle\frac{λ}{2}×(2m+1)-2Δd\)

    \(x=\displaystyle\frac{λL(2m+1)}{4h}-\displaystyle\frac{LΔd}{h}\)

    こうして、ガラスを下に動かすことによって得られる明線の位置がわかりました。なお以前に計算した通り、ガラスを動かさない場合、\(x\)の位置は以下になります。

    \(x=\displaystyle\frac{λL(2m+1)}{4h}\)

    2つの答えを比較すると、ガラスを下に移動させることにより、\(x\)の位置は\(-\displaystyle\frac{LΔd}{h}\)ずれているとわかります。つまり、\(x\)の位置は左へ\(\displaystyle\frac{LΔd}{h}\)移動します。

    2) 明線の間隔\(Δx\)はどのように変化しますか

    明線の条件を利用し、\(m\)番目と\(m+1\)番目の線について間隔を計算しましょう。以下のようになります。

    \(x=\displaystyle\frac{λL(2m+3)}{4h}-\displaystyle\frac{LΔd}{h}\)\(-\left(\displaystyle\frac{λL(2m+1)}{4h}-\displaystyle\frac{LΔd}{h}\right)\)

    \(Δx=\displaystyle\frac{λL}{2h}\)

    先ほどの結果と今回の計算結果を比較すると、「明線の間隔に変化はない」とわかりました。

    3) ガラスの移動による明線の移動距離が\(l\)のとき、ガラスの下降距離を求めましょう

    これまでの計算結果より、ガラスを下へ\(Δd\)移動させることにより、\(x\)の位置が左へ\(\displaystyle\frac{LΔd}{h}\)ずれるとわかっています。明線の移動距離が\(l\)であるため、以下の式を作りましょう。

    \(l=\displaystyle\frac{LΔd}{h}\)

    \(Δd=\displaystyle\frac{lh}{L}\)

    こうして、ガラスの移動距離\(Δd\)は\(\displaystyle\frac{lh}{L}\)と計算できました。

    くさび形空気層の構造と干渉条件を計算する

    波の干渉条件の中でも、くさび形空気層は光路差の計算が容易です。ただくさび形空気層で明線または暗線の条件を得るとき、屈折率を考慮しましょう。反射場所によって自由端反射と固定端反射が異なるのです。

    反射の種類を確認すれば、明線条件と暗線条件を出すことができます。公式を覚えても問題を解けないため、必ず公式の出し方を学びましょう。

    なおくさび形空気層の問題を解くとき、真上からではなく、真下にスクリーンを置くケースがあります。また、ガラスを移動させる問題が出されることもあります。こうしたとき、どのように値が変化するのか計算できるようになりましょう。

    公式の出し方や屈折率の違いによる反射の原理を理解すれば、すべての応用問題を解くことができます。なぜ波の干渉が起こるのかを学び、くさび形空気層に関する問題を解けるようになりましょう。