極限を学ぶことにより、関数の連続性がわかります。関数の連続性では、線が途中で途切れているかどうかを確認すればいいです。
ただ、途切れているかどうかでは説明として不十分です。範囲を区切れば、関数が連続しているケースは多いです。そこで、極限を用いることで関数の連続性を定義するのです。
なお、連続関数には性質があります。その一つの性質が中間値の定理です。内容を覚える必要はなく、当たり前のことを述べているにすぎませんが、どのような定理なのか事前に理解する必要があります。
それでは、極限を用いてどのように関数の連続性を確認すればいいのでしょうか。関数の連続性について解説していきます。
もくじ
連続な関数は途中で途切れていない
私たちが極限を学ぶ理由として、微分を学ぶ必要があるからです。微分は極限を利用して定義されます。
また、微分は傾きを得るために利用されます。関数が途切れている場合、途切れている点において、傾きは存在しません。一方で線が連続してつながっている場合、傾きが存在することになります。
このとき、一次関数や二次関数は連続な関数です。
いずれにしても、途中で途切れていない関数は連続な関数といえます。
極限を用いて関数の連続性を定義する
一方、反比例のグラフは多くの部分で連続しているものの、連続していない部分もあります。例えば\(y=\displaystyle\frac{1}{x}\)では、\(x=0\)の部分で途切れています。
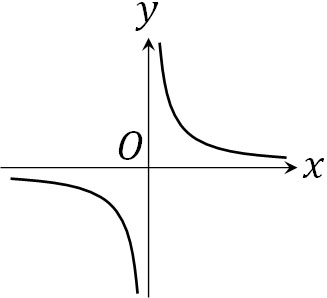
この場合、\(y=\displaystyle\frac{1}{x}\)は\(x=0\)の部分で不連続です。ただその他の部分では連続になっているため、反比例のグラフは特定の区間で連続です。
それでは、極限を用いてどのように連続と不連続を見分ければいいのでしょうか。以下の条件について、いずれか一方を満たしている場合、\(x=a\)のときに不連続となります。
- \(\displaystyle \lim_{ x \to a } f(x)\)に極限がない
- \(\displaystyle \lim_{ x \to a } f(x)=f(a)\)ではない
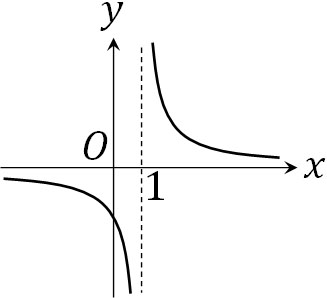
例えば\(\displaystyle \lim_{ x \to 1+0 } \displaystyle\frac{1}{x-1}=∞\)であり、\(\displaystyle \lim_{ x \to 1-0 } \displaystyle\frac{1}{x-1}=-∞\)です。このように\(\displaystyle \lim_{ x \to a+0 } f(x)≠\displaystyle \lim_{ x \to a-0 } f(x)\)のとき、\(x=a\)で極限が存在しないと考えます。
また\(\displaystyle \lim_{ x \to a } f(x)\)について極限が存在しても、\(\displaystyle \lim_{ x \to a } f(x)=f(a)\)でない場合は不連続です。以下のグラフは「極限が存在するものの、\(\displaystyle \lim_{ x \to a } f(x)=f(a)\)ではないケース」に該当します。
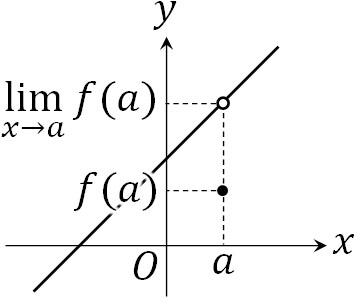
いずれにしても、極限を用いることで関数が連続かどうかを確認できます。
ガウス記号を用いる図形と関数の連続性
関数の連続性を学ぶとき、ガウス記号を用いる関数を習うことがあります。ガウス記号を用いる関数は重要ではないものの、関数の連続性を学ぶときに有用なのです。例として、\(f(x)=[x]\)のグラフを描きましょう。
\(f(x)=[x]\)では、\(n≦x<n+1\)となるとき、\([x]=n\)と定義します。例えば1.23は\(1≦1.23<2\)であるため、\([1.23]=1\)です。同様に考えると、\([0.1]=0\)となり、\([-2.3]=-3\)となります。そのため、以下のグラフになります。

\(f(x)=[x]\)について、例えば\(x=2\)のとき、関数は不連続です。これは、\(\displaystyle \lim_{ x \to 2+0 } f(x)≠\displaystyle \lim_{ x \to 2-0 } f(x)\)であるため、極限が存在しないからです。
関数の連続性を調べる
それでは、練習問題を解くことによって関数の連続性を確認しましょう。以下の関数について、\(x=-1\)での連続性を調べましょう。
- \(f(x)=\displaystyle\frac{x(x+1)}{x^2-1}\)\((x≠-1)\)
- \(f(-1)=\displaystyle\frac{1}{2}\)
以下のように計算します。
\(\displaystyle \lim_{ x \to -1 } \displaystyle\frac{x(x+1)}{x^2-1}\)
\(=\displaystyle \lim_{ x \to -1 } \displaystyle\frac{x(x+1)}{(x+1)(x-1)}\)
\(=\displaystyle \lim_{ x \to -1 } \displaystyle\frac{x}{x-1}\)
\(=\displaystyle\frac{1}{2}\)
\(\displaystyle \lim_{ x \to -1 } \displaystyle\frac{x(x+1)}{x^2-1}\)は極限があり、それに加えて\(\displaystyle \lim_{ x \to -1 } \displaystyle\frac{x(x+1)}{x^2-1}=f(-1)\)です。そのため、\(f(x)\)は\(x=-1\)で連続です。
閉区間で連続な場合、最大値と最小値をもつ
関数が途中で途切れていたとしても、特定の区間では連続であるケースは多いです。このとき、\(x\)の範囲を\(a≦x≦b\)とする場合、この特定の区間を閉区間といいます。
閉区間で関数が連続である場合、関数の両端を含むすべての値で\(y\)の値が存在するため、必ず最小値と最大値があります。これについては、特に説明しなくても理解できると思います。ただ閉区間であっても、関数が連続でない場合、最小値または最大値を得られないケースがあります。
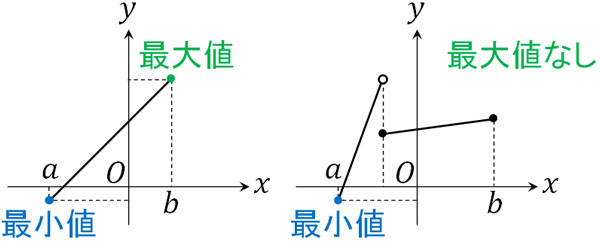
関数の計算をするとき、最小値や最大値を問う問題は多いです。このとき、関数が連続であることは非常に重要なのです。
中間値の定理:閉区間で連続な関数は解をもつ
閉区間で連続な関数について、ほかの性質を学びましょう。関数\(f(x)\)が\(a≦x≦b\)\((a≠b)\)で連続の場合、\(f(a)<k<f(b)\)となる任意の値\(k\)について、\(f(c)=k\)を満たす\(c\)が必ず\(a\)と\(b\)の間にあります。
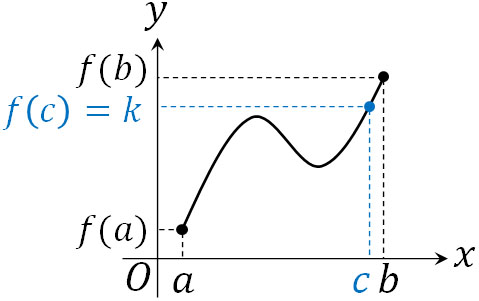
これを中間値の定理といいます。中間値の定理についても、説明しなくても理解できると思います。グラフの形はわからないし、いくつの解をもつのかも不明であるものの、少なくとも一つは解をもつのです。
一方、特定の点で関数が不連続の場合、必ず\(f(c)=k\)を満たす\(c\)が存在するとは限りません。以下のケースが存在するからです。
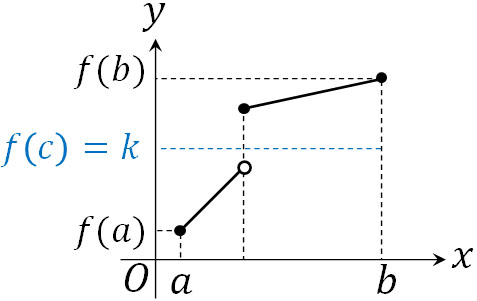
それでは中間値の定理を利用することにより、問題を解いてみましょう。
- \(4^x=3x+2\)について、\(1<x<2\)の間に少なくとも一つの実数解をもつことを示しましょう。
\(f(x)=4^x-3x-2\)としましょう。\(4^x-3x-2=0\)を満たす\(x\)が存在する場合、解をもつことになります。また\(f(1)<0,f(2)>0\)または\(f(1)>0,f(2)<0\)の場合、関数が連続なのであれば、\(1<x<2\)の間で\(4^x-3x-2=0\)となる\(x\)の値が必ず存在します。
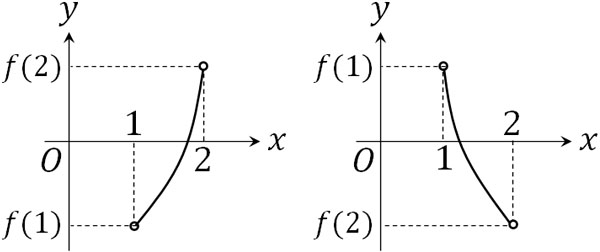
グラフの形は不明であっても、解が存在するかどうかわかればいいです。そこで、\(f(1)\)と\(f(2)\)を計算しましょう。
- \(f(1)=4-3-2=-1\)
- \(f(2)=16-6-2=8\)
\(f(1)<0,f(2)>0\)であるため、\(f(x)=4^x-3x-2\)は\(1<x<2\)の間に少なくとも一つの実数解をもちます。こうして\(4^x=3x+2\)について、\(1<x<2\)の間に少なくとも一つの実数解をもつことを証明できました。
極限を利用して関数の連続性を確認する
関数が連続か不連続かというのは、関数が途切れているかどうかで判断できます。不連続の場合、関数はどこかの値で途切れます。
そこで関数が不連続となる場合について、極限を用いて定義します。\(\displaystyle \lim_{ x \to a+0 } f(x)≠\displaystyle \lim_{ x \to a-0 } f(x)\)のとき、関数は\(x=a\)で不連続です。\(\displaystyle \lim_{ x \to a } f(x)=f(a)\)ではないケースについても、関数は\(x=a\)で不連続です。
なお、関数の連続性には性質があります。閉区間で関数が連続な場合、必ず最小値と最大値があります。また、中間値の定理を利用して解が存在することを証明できるようになりましょう。
関数の計算をするとき、連続な関数をメインで利用して計算してきました。関数の連続性というのは、極限を利用することで表すことができるのです。






