対数の性質：定義や足し算・引き算、底の変換公式

統計データでひんぱんに利用される概念が対数です。指数と対数は親せきの関係であり、指数を対数へ変換することができます。

そこで、対数の計算を行えるようになりましょう。対数の定義と性質を覚えることにより、対数同士の足し算や引き算を行えるようにするのです。また、底の変換公式を利用することにより、対数の底を変えられるようになりましょう。

対数の性質を理解すれば、指数と対数を含む式の計算が可能になります。両辺に対数を加えることによって計算するのです。

それでは、対数の性質には何があるのでしょうか。また、どのように公式を利用しての問題を解けばいいのでしょうか。対数の定義や公式、計算方法を解説していきます。

対数を学ぶ理由は何か？

数字を\(n\)乗する場合、\(n\)の値が大きいと、結果は非常に大きい値になります（または、計算結果は小さい値になります）。例えば\(2^3\)を計算すると答えは8ですが、\(2^{30}\)だと答えは1,073,741,824となり、10億よりも大きい値が答えになります。

そのため指数を利用する統計データでは、図を確認しても何を表しているのか判断するのが難しいです。例えば\(2^5\)や\(2^{10}\)の結果というのは、\(2^{30}\)の結果に比べて非常に小さい値であるため、グラフでは\(2^5\)も\(2^{10}\)も0付近に存在するように見えてしまうのです。

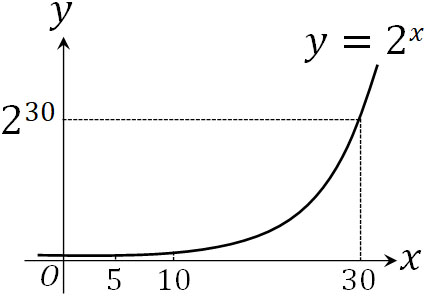
ただ実際の統計データでは、当然ながら小さい値も大きな意味があります。そこで、対数が利用されます。特定の値（底）に対して、何乗したのかを表すのが対数です。例えば\(2^5\)では5乗しており、\(2^{30}\)では30乗しています。

そこで\(y=2^x\)について、両辺に対して対数（\(log_2\)）を加えましょう。この場合、グラフは以下になります。

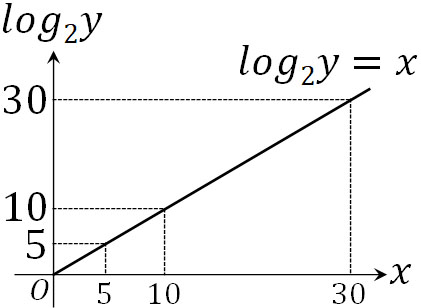
\(y\)軸の値（\(log_2\)\(y\)）が5と30であれば、グラフを確認することで明確に区別できます。指数関数では判断しにくいものの、対数関数であれば区別できるのです。これが、指数関数と同時に対数関数を学ばなければいけない理由です。

統計データで指数が利用されるため、対数も統計データでひんぱんに利用されます。科学実験で対数が利用されるだけでなく、日々のニュースでも対数を利用しているデータが活用されます。

対数の定義と性質：指数と対数の変換

それでは、対数の定義は何なのでしょうか。指数に対して、以下のように対数を定義しましょう。

• \(a^p=m↔p=log_aM\)

※\(a>0\)、\(a≠1\)、\(M>0\)

この定義を覚える必要はありません。対数の性質を学べば、容易に指数を対数へ変えることができるからです。また、対数を指数へ変換する簡単な方法も存在します。

\(log_aM\)について、\(a\)を底、\(M\)を真数といいます。例えば\(log_28\)の底は2、真数は8です。2（底）を何乗すれば、8（真数）になるでしょうか。\(8=2^3\)であるため、2（底）を3乗すれば、8（真数）になります。そのため、\(log_28=log_22^3=3\)です。そこで、以下のように考えましょう。

• \(log_21=log_22^0=0\)
• \(log_22=log_22^1=1\)
• \(log_24=log_22^2=2\)
• \(log_28=log_22^3=3\)
• \(log_216=log_22^4=4\)

それでは、対数の性質を一般化して学びましょう。対数の性質として、指数を対数の前に置けます。

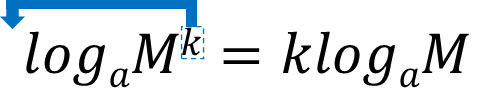
この性質は非常に重要であるため、必ず覚えましょう。また、底を何乗すれば真数になるのかを表すのが底であるため、以下の計算をすることができます。

• \(log_aa=log_aa^1=1\)
• \(log_a1=log_aa^0=0\)
• \(log_a\displaystyle\frac{1}{a}=log_aa^{-1}=-1\)

なお対数を利用するとき、非常に重要な方法があります。それは、両辺に対して任意の底をもつ対数を加えることができることです。そこで\(a^p=M\)について、両辺に\(log_a\)を加えましょう。

\(a^p=M\)

\(\color{red}{log_a}a^p=\color{red}{log_a}M\)

\(plog_aa=log_aM\)

\(p=log_aM\)

式を確認すると、先ほどの定義とまったく同じであることがわかります（\(a^p=m\)\(↔p=log_aM\)）。指数に対して、特定の底をもつ対数を加えられることを学びましょう。

左辺と右辺が同じ値なのであれば、同じ底をもつlogを両辺に加えても、左辺と右辺の値は同じになります。この性質を利用すれば、指数を対数へ変換できるのです。

また、対数を指数へ変換することもできます。この場合、\(log_aa=1\)を利用しましょう。\(p=log_aM\)を指数に変換する場合、以下のように計算します。

\(p=log_aM\)

\(p\color{red}{log_aa}=log_aM\)

\(log_aa^p=log_aM\)

\(a^p=M\)

こうして、対数の定義を覚えることなく、対数を指数へ変換することができました。指数を対数へ変換したり、対数を指数へ変えたりする計算はひんぱんに利用するため、必ず行えるようになりましょう。

対数の足し算と引き算（かけ算と割り算）の計算方法

他に重要な対数の性質が足し算と引き算です。対数同士で足し算や引き算をするとき、どのような計算になるのか学びましょう。具体的には、真数のかけ算は対数の足し算になります。また、真数の割り算は対数の引き算になります。

• \(log_aMN=log_aM+log_aN\)
• \(log_a\displaystyle\frac{M}{N}=log_aM-log_aN\)

これらは対数の性質であり、覚えないと対数の計算をすることができません。そのため、必ず覚える必要があります。それでは、以下の計算をしてみましょう。

• \(4log_2\sqrt{6}-2log_23\)

これまでの説明内容を理解していれば、この式を計算することができます。

\(4log_2\sqrt{6}-2log_23\)

\(=4log_26^{\frac{1}{2}}-2log_23\)

\(=log_26^{\frac{4}{2}}-log_23^2\)

\(=log_26^2-log_29\)

\(=log_236-log_29\)

\(=log_2\displaystyle\frac{36}{9}\)

\(=log_24\)

\(=log_22^2\)

\(=2log_22\)

\(=2\)

こうして、答えは2とわかりました。

・底と真数が同じ場合、足し算が可能

なお底と真数が同じ場合、対数の前にある数字を足しましょう。例えば、以下のようになります。

\(2log_35+3log_35=5log_35\)

対数を利用して足し算をするとき、対数の前にある数字はかけ算ではなく足し算になります。

底の変換公式を使い、対数計算での底を変える

なお、公式を利用することによって対数計算での底を変えることができます。\(a,b,c\)が正の数であり、\(a≠1\)、\(b≠1\)、\(c≠1\)のとき、以下の公式が成り立ちます。

• \(lob_ab=\displaystyle\frac{log_cb}{log_ca}\)

つまり、任意の底をもつ対数（\(log_c\)）を利用することにより、底を変えることができるのです。証明方法は簡単であり、\(a^r=b\)に対して、\(c\)を底とする対数を両辺に取ります。

\(a^r=b\)

\(log_ca^r=log_cb\)

\(rlog_ca=log_cb\)

\(r=\displaystyle\frac{log_cb}{log_ca}\)

また、\(a^r=b\)を\(r=log_ab\)へ変換できます。これは、対数の定義でもあります。

\(a^r=b\)

\(log_aa^r=log_ab\)

\(rlog_aa=log_ab\)

\(r=log_ab\)

そのため、\(lob_ab=\displaystyle\frac{log_cb}{log_ca}\)となります。それでは、次の式を計算してみましょう。

• \((log_29+log_43)log_34\)

方針としては、底をそろえましょう。底をそろえないと、対数同士の足し算や引き算（かけ算や割り算）をすることができないからです。そこで、底の変換公式を利用することによって以下のように計算します。

\((log_29+log_43)log_34\)

\(=\left(log_23^2+\displaystyle\frac{log_23}{log_24}\right)\displaystyle\frac{log_24}{log_23}\)

\(=\left(2log_23+\displaystyle\frac{log_23}{log_22^2}\right)\displaystyle\frac{log_22^2}{log_23}\)

\(=\left(2log_23+\displaystyle\frac{1}{2}log_23\right)\displaystyle\frac{2}{log_23}\)

\(=\displaystyle\frac{5}{2}log_23·\displaystyle\frac{2}{log_23}\)

\(=5\)

こうして、底を2にそろえることによって答えを得ることができました。

指数と対数を含む式の計算

対数の性質を学んで計算方法を理解したら、指数と対数を含む式の計算を行えるようになりましょう。例題として、以下の式の値を計算しましょう。

• \(4^{log_27}\)

これまで説明した通り、指数を対数へ変換することができます。また指数を含む等式では、両辺に対数を加えることによって計算できることが多いです。そこで\(4^{log_27}=M\)と考えて計算しましょう。

計算方法としては、両辺に対数を加えます。どのような底をもつ対数を利用すればいいのか悩みますが、対数の計算では底をそろえるのが一般的です。式に\(log_27\)が存在するため、同様に底が2の対数を利用して計算しましょう。

\(4^{log_27}=M\)

\(log_24^{log_27}=log_2M\)

\(log_27·log_24=log_2M\)

\(log_27·log_22^2=log_2M\)

\(2log_27=log_2M\)

\(log_27^2=log_2M\)

\(log_249=log_2M\)

\(49=M\)

こうして、\(4^{log_27}=49\)とわかりました。ここまで説明した内容を理解していれば、問題なく答えを得ることができます。

対数の性質を学び、計算できるようにする

指数と同様に重要な概念が対数です。指数と対数は親せきであり、指数を対数へ変換することができます。

対数の定義を利用できるようになる必要はありません。ただ対数を利用して、指数を対数へ変えたり、対数を指数へ変換したりできるようになりましょう。

なお対数を利用して計算するとき、底をそろえるのが一般的です。そこで対数を加えるとき、同じ底をもつ対数を利用しましょう。また底の変換公式を利用し、底をそろえられるようになりましょう。この考え方を理解すれば、指数と対数を含む式の計算も可能です。

対数は重要な計算方法であり、利用される場面は多いです。そこで対数の意味を学び、対数を利用して計算できるようになりましょう。