三角関数の極限：公式、置き換え、はさみうちの原理での計算

関数の極限を計算するとき、三角関数の極限を計算しなければいけないことがあります。三角関数の極限の計算では、公式を利用しましょう。公式を利用できない場合であっても、式を変形することによって公式を利用できるようにする必要があります。

三角関数の極限に関する公式は覚えなければいけません。そのつど、証明をすると時間がかかるからです。ただ、どのようにして公式を得るのか理解しましょう。

また、公式を利用することで計算問題を解けるようにならなければいけません。そこで式を変形したり、置き換えを利用したりすることで答えを得ましょう。

それでは、どのように三角関数の極限の問題を解けばいいのでしょうか。公式の証明や利用法を解説していきます。

1 三角関数の極限で利用される公式
- 1.1 公式の証明を行う
2 公式を利用して三角関数の極限を計算する
- 2.1 置き換え・はさみうちの原理を利用する三角関数の極限の計算
3 公式を利用して三角関数の極限を得る

三角関数の極限で利用される公式

三角関数の極限を計算するとき、\(\displaystyle \lim_{ x \to 0 } sin\ x=0\)や\(\displaystyle \lim_{ x \to 0 } cos\ x=1\)は容易に理解できます。それでは、\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ 2x}{x}\)はどのように計算すればいいのでしょうか。

三角関数の極限では公式があり、以下の公式を利用します。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ x}{x}=1\)
\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{x}{sin\ x}=1\)

この公式を利用すれば、以下のように計算できます。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ 2x}{x}\)

\(=\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ 2x}{2x}·2\)

\(=1×2\)

\(=2\)

こうして、答えを得ることができました。

公式の証明を行う

それでは、なぜ先ほど記した公式が成り立つのでしょうか。公式の証明をしましょう。まず、以下のように二等辺三角形である△OABと扇形OABを作ります。

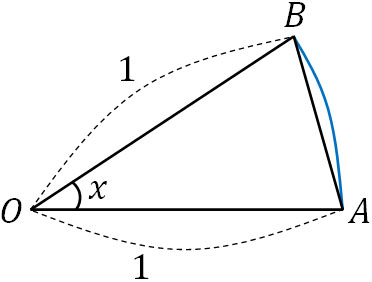
△OABの面積は\(\displaystyle\frac{1}{2}×1×1×sin\ x=\displaystyle\frac{sin\ x}{2}\)です。それでは、扇形OABの面積はいくらでしょうか。扇形の面積は半径\(r\)と中心角\(θ\)で決まります。\(r^2×\displaystyle\frac{θ}{360}\)が扇形の面積になりますが、角度が弧度法の場合、\(r^2×\displaystyle\frac{θ}{2}\)が扇形の面積です。

そのため弧度法を利用すると、上図での扇形の面積は\(1^2×\displaystyle\frac{x}{2}=\displaystyle\frac{x}{2}\)です。△OABの面積よりも扇形の面積のほうが大きいため、以下の関係が成り立ちます。

\(\displaystyle\frac{sin\ x}{2}<\displaystyle\frac{x}{2}\)

次に、以下の図形を作りましょう。

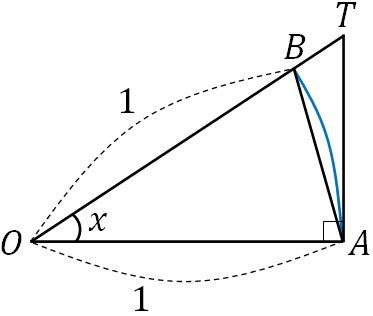
辺ATの長さは\(tanx\)であるため、△OATの面積は\(\displaystyle\frac{tanx}{2}\)です。扇形の面積よりも△OATの面積のほうが大きいため、以下の関係式を作りましょう。

\(\displaystyle\frac{sin\ x}{2}<\displaystyle\frac{x}{2}<\displaystyle\frac{tanx}{2}\)

そこで、以下のように式を変形します。

\(\displaystyle\frac{sin\ x}{2}<\displaystyle\frac{x}{2}<\displaystyle\frac{tanx}{2}\)

\(sin\ x<x<tanx\)

\(\displaystyle\frac{1}{tanx}<\displaystyle\frac{1}{x}<\displaystyle\frac{1}{sin\ x}\)

\(\displaystyle\frac{sin\ x}{tanx}<\displaystyle\frac{sin\ x}{x}<\displaystyle\frac{sin\ x}{sin\ x}\)

\(cosx<\displaystyle\frac{sin\ x}{x}<1\)

\(\displaystyle \lim_{ x \to 0 } cosx=1\)であるため、はさみうちの原理より、\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ x}{x}=1\)です。こうして、公式を証明できました。

・\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{x}{sin\ x}=1\)を得る

なお、先ほど計算した公式を利用して\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{x}{sin\ x}=1\)となることを証明しましょう。以下のように式を変形します。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{x}{sin\ x}\)

\(=\displaystyle \lim_{ x \to 0 } \displaystyle\frac{1}{\displaystyle\frac{sin\ x}{x}}\)

\(=\displaystyle\frac{1}{1}\)

\(=1\)

こうして、\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{x}{sin\ x}=1\)になるとわかりました。

公式を利用して三角関数の極限を計算する

それでは、先ほど証明した公式を利用して三角関数の極限を計算しましょう。以下の問題の答えは何でしょうか。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{tan\ x}{x}\)

以下のように計算しましょう。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{tan\ x}{x}\)

\(=\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ x}{x}·\displaystyle\frac{1}{cos\ x}\)

\(=1×\displaystyle\frac{1}{1}\)

\(=1\)

また、次の問題の答えは何でしょうか。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{1-cos\ x}{x^2}\)

以下のように計算しましょう。

\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{1-cos\ x}{x^2}\)

\(=\displaystyle \lim_{ x \to 0 } \displaystyle\frac{1-cos\ x}{x^2}·\displaystyle\frac{1+cos\ x}{1+cos\ x}\)

\(=\displaystyle \lim_{ x \to 0 } \displaystyle\frac{1-cos^2\ x}{x^2}·\displaystyle\frac{1}{1+cos\ x}\)

\(=\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin^2\ x}{x^2}·\displaystyle\frac{1}{1+cos\ x}\)

\(=1×\displaystyle\frac{1}{1+1}\)

\(=\displaystyle\frac{1}{2}\)

こうして、公式を利用することで三角関数の極限を計算できました。

置き換え・はさみうちの原理を利用する三角関数の極限の計算

一見すると先ほど証明した公式を利用できないケースがあります。この場合、置き換えを利用することで公式を利用できるようにしましょう。つまり、何とかして\(\displaystyle \lim_{ x \to 0 } \displaystyle\frac{sin\ x}{x}=1\)を使うのです。

練習問題として以下の問題を解きましょう。

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{sin\ πx}{x-1}\)
\(\displaystyle \lim_{ x \to \frac{π}{2} } \displaystyle\frac{cos\ x}{2x-π}\)
\(\displaystyle \lim_{ x \to ∞ } xsin\displaystyle\frac{1}{x}\)
\(\displaystyle \lim_{ x \to 0 } x^2sin\displaystyle\frac{1}{x}\)

なお場合によっては、公式を利用せず、はさみうちの原理を利用することで問題を解かなければいけないこともあります。

1) \(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{sin\ πx}{x-1}\)

\(x \to 0\)ではなく、\(x \to 1\)となっています。この場合、\(t=x-1\)とすると、\(x \to 1\)のときに\(t \to 0\)となります。なお\(x=t+1\)であるため、以下のように計算しましょう。

\(\displaystyle \lim_{ x \to 1 } \displaystyle\frac{sin\ πx}{x-1}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{sin\ π(t+1)}{(t+1)-1}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{sin\ (πt+π)}{t}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{-sin\ πt}{t}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{sin\ πt}{πt}·-π\)

\(=-π\)

2) \(\displaystyle \lim_{ x \to \frac{π}{2} } \displaystyle\frac{cos\ x}{2x-π}\)

先ほどと同様に考えて計算しましょう。\(t=x-\displaystyle\frac{π}{2}\)とすると、\(x \to \displaystyle\frac{π}{2}\)によって\(t \to 0\)になります。また、\(x=t+\displaystyle\frac{π}{2}\)です。

\(\displaystyle \lim_{ x \to \frac{π}{2} } \displaystyle\frac{cos\ x}{2x-π}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{cos\ \left(t+\displaystyle\frac{π}{2}\right)}{2t}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{-sin\ t}{2t}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{sin\ t}{t}·-\displaystyle\frac{1}{2}\)

\(=-\displaystyle\frac{1}{2}\)

3) \(\displaystyle \lim_{ x \to ∞ } xsin\displaystyle\frac{1}{x}\)

\(t=\displaystyle\frac{1}{x}\)とすると、\(x \to ∞\)のとき、\(t \to 0\)となります。そのため、以下のように式を変形できます。

\(\displaystyle \lim_{ x \to ∞ } xsin\displaystyle\frac{1}{x}\)

\(=\displaystyle \lim_{ t \to 0 } \displaystyle\frac{sin\ t}{t}\)

\(=1\)

4) \(\displaystyle \lim_{ x \to 0 } x^2sin\displaystyle\frac{1}{x}\)

ここまで、公式を利用することによって答えを得られる式を解説してきました。ただ場合によっては、公式を利用しても答えを得られないケースがあります。この場合、はさみうちの原理を利用することで計算することを考えましょう。

\(-1≦sin\displaystyle\frac{1}{x}≦1\)です。また\(x≠0\)であるため、以下のように計算しましょう。

\(-1≦sin\displaystyle\frac{1}{x}≦1\)

\(-x^2≦x^2sin\displaystyle\frac{1}{x}≦x^2\)

\(\displaystyle \lim_{ x \to 0 } -x^2=0\)であり、\(\displaystyle \lim_{ x \to 0 } x^2=0\)です。そのため、はさみうちの原理より\(\displaystyle \lim_{ x \to 0 } x^2sin\displaystyle\frac{1}{x}=0\)です。