高校数学で学ぶ内容の一つに三角形の定理があります。三角形には必ず外接円や内接円があります。また、三角形には垂心や重心もあります。これらの性質を利用することによって辺の長さを計算したり、証明問題を解いたりするのです。
ただ、それぞれの定理は独立しています。三角形を利用することは共通しているものの、すべての定理の内容を覚えなければいけません。三角形の定理を覚えていない場合、問題を解くことができないのです。
また三角形の定理を利用する問題では、複合問題がひんぱんに出されます。そのため、複数の定理を利用することで問題を解かなければいけないことがよくあります。
それでは、三角形の定理にはどのようなものがあるのでしょうか。三角形がもつ定理について解説していきます。
もくじ
三角形がもつ5つの定理
すべての三角形に共通する定理が存在します。最も重要な図形の一つが三角形であり、数学の問題では三角形がひんぱんに出されます。また前述の通り、三角形の定理を覚えていないと問題を解けないことは多いです。
三角形の定理には主に以下の5つがあります。
- 三角形の外心の定理
- 三角形の垂心の定理
- 三角形の内心の定理
- 三角形の重心の定理
- 中線定理
そこで、これらの定理の内容を覚えましょう。
三角形の外心の定理:三角形の外接円
すべての三角形には外接円があります。以下のように、三角形の外に接する円を必ず描くことができるのです。
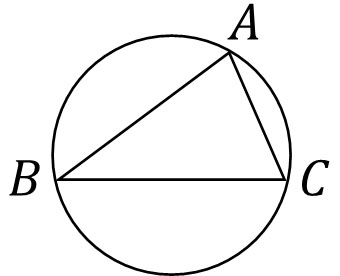
そこで、それぞれの辺について、垂直二等分線を引きましょう。そうすると、垂直二等分線は必ず一点で交わります。より詳しくいうと、垂直二等分線は外接円の中心Oで交わります。
また点Oは外接円の中心であるため、OA=OB=OCです。また三角形にとって、点Oを外心といいます。外接円を基準にすると、点Oは円の中心です。一方、三角形を基準にすると点Oは外心という名前になるのです。

それでは、三角形の外心を利用して問題を解いてみましょう。以下の図で△ABCの外心をOとするとき、\(∠a\)と\(∠b\)の大きさはいくらでしょうか。
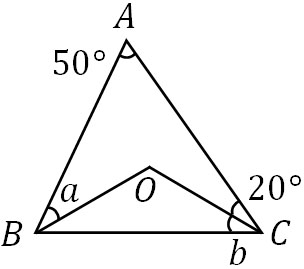
外心Oというのは、外接円の中心でもあります。そのためOA=OB=OCであり、3つの二等辺三角形を作ることができます。以下の図のようになります。
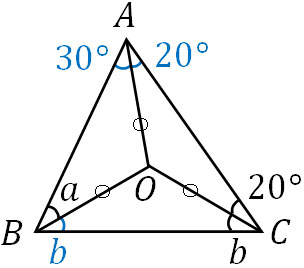
こうして、\(∠a=30°\)とわかります。また三角形の内角の和は180°なので、以下の式を作ることができます。
\(180=60+40+2b\)
\(2b=80\)
\(b=40\)
こうして、\(∠b=40°\)とわかりました。
三角形の垂心の定理:頂点から垂直に線をおろす
先ほど、辺の垂直二等分線を利用しました。次は、それぞれの頂点から辺に対して垂直になるように線を引きましょう。以下のようになります。
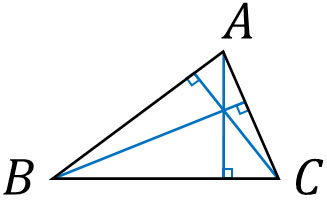
このとき、3つの直線は一点で交わります。この点を垂心といいます。
三角形の定理の中では、三角形の垂心は重要ではありません。垂心を利用して問題を解くケースは少ないです。ただ、垂心の意味を理解しましょう。三角形の垂心を通る直線では、辺と交わる部分は必ず直角になります。
三角形の内心の定理:三角形の内接円
次に三角形の内心を学びましょう。三角形に必ず外接円があるのと同じように、すべての三角形は内接円をもちます。以下のように、三角形の内側に円を作ることができるのです。
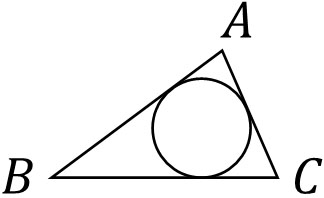
内接円の中心を点Oとします。このとき、三角形の角の二等分線は必ず点Oを通ります。内接円を基準にすると、点Oは円の中心です。一方で三角形を基準にすると、点Oを内心といいます。
また点Oは円の中心であるため、内心から辺に対して垂直に線を引く場合、すべての辺の長さは等しくなります。
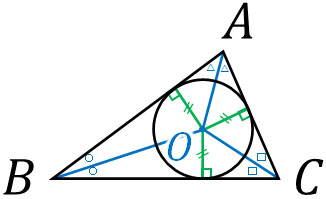
それでは、三角形の内心を利用して問題を解いてみましょう。以下の問題の答えは何でしょうか。
- AB=6、BC=5、AC=4の△ABCがあります。点Oが△ABCの内心の場合、AO:ODを求めましょう。
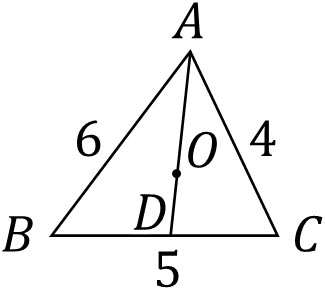
点Oが三角形の内心であるため、∠BAD=∠CADです。角の二等分線の定理より、AB:AC=BD:DCです。そのため、BD:DC=6:4=3:2です。
この結果より、BDの長さを計算しましょう。BD:DC=3:2であるため、BD=3です。
\(BD=5×\displaystyle\frac{3}{5}=3\)
次に△ABDに着目しましょう。
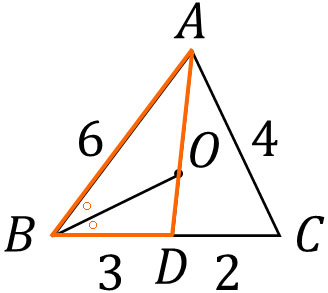
三角形の内心の定理より、∠ABO=∠DBOです。そのため角の二等分線の定理より、BA:BD=AO:ODです。そのため、以下のように答えを得ることができます。
\(BA:BD=6:3=2:1\)\(=AO:OD\)
こうして、AO:OD=2:1であるとわかりました。三角形の内心の定理に加えて、角の二等分線の定理を利用することで今回の問題の答えを得ることができます。
三角形の重心の定理:2:1に内分する点
三角形で重心を利用する定理は重要です。頂点から辺の中点に対して線を引くとき、3点が交わる点を重心といいます。以下の点が重心になります。
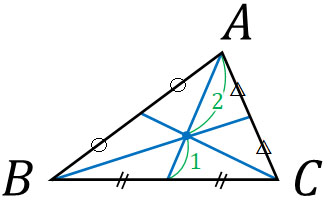
重心を通る線というのは、線の比が必ず2:1になります。これを三角形の重心の定理といいます。それでは、重心を利用した問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 点Oは△ABCの重心です。△OBDの面積が4の場合、△ABCの面積はいくらでしょうか。
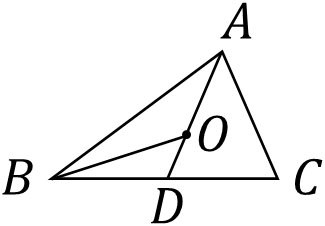
前述の通り、重心を通る直線は辺を二等分します。つまり、BDを2倍するとBCになります。高さは同じであるものの、横の長さが二倍になるため、△OBCの面積は8です。
\(△OBC=4×2=8\)
また点Oは重心なので、AO:OD=2:1です。つまり、AD:OD=3:1です。△OBCと△ABCを比べると、横の長さは同じであるものの、△ABCは3倍の高さがあります。そのため、△ABCの面積は24です。
\(△ABC=8×3=24\)
中線定理(パップスの定理):中点を利用する定理
三角形の頂点と辺の中点を結んだ線に関する定理として中線定理(パップスの定理)があります。馴染みの薄い定理ではあるものの、中線定理を知っていれば、図形の問題が出されたときに解答時間を大幅に短縮できるメリットがあります。
△ABCについて、辺BCの中点をDとするとき、以下の関係が成り立ちます。
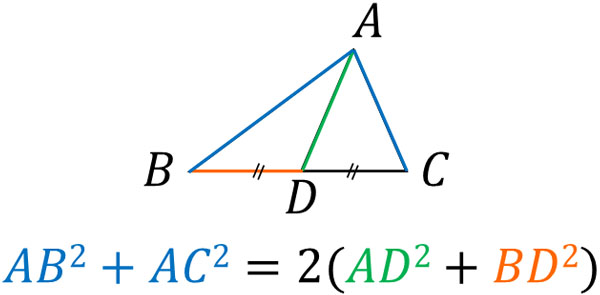
BD=CDなので、\(AB^2+AC^2\)\(=2(AD^2+CD^2)\)も成り立ちます。要は「辺の長さを二乗して足す場合、中線の二乗と底辺の半分の二乗を足し、2倍すると同じ値になる」と覚えましょう。なお、中線定理は三平方の定理や余弦定理、ベクトルなど、さまざまな方法を利用して証明することができます。
それでは、中線定理を利用して問題を解いてみましょう。以下の問題の答えは何でしょうか。
- △ABCについて、点DはBCの中点です。AB=5、AC=3、∠BAC=60°のとき、ADの長さを求めましょう。
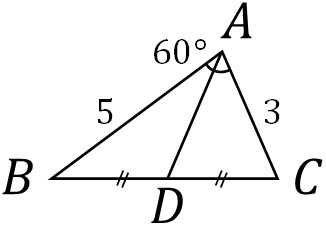
2辺の長さと角度がわかっているため、余弦定理を利用してBCの長さを出しましょう。
\(BC^2=AB^2+AC^2\)\(-2AB×AC×cos60°\)
\(=25+9-30×\displaystyle\frac{1}{2}\)
\(=19\)
\(BC>0\)なので、\(BC=\sqrt{19}\)です。また点DはBCの中点なので、\(BD=\displaystyle\frac{\sqrt{19}}{2}\)です。
次に、中線定理を用いてADの長さを出しましょう。
\(AB^2+AC^2=2(AD^2+BD^2)\)
\(25+9=2(AD^2+\displaystyle\frac{19}{4})\)
\(34=2AD^2+\displaystyle\frac{19}{2})\)
\(4AD^2=68-19\)
\(AD^2=\displaystyle\frac{49}{4}\)
\(AD=\displaystyle\frac{7}{2}\)\((AD>0)\)
こうして、\(AD=\displaystyle\frac{7}{2}\)が答えとわかりました。
三角形の定理を覚え、辺の長さや比を計算する
最も重要な図形の一つが三角形です。高校数学では、三角形の性質を覚えていないと問題を解けない場合が多いです。そこで、ここまで解説した5つの三角形の定理をすべて覚えましょう。
三角形には外心や垂心、内心、重心があります。それぞれ性質が異なるため、どのような特徴があるのか把握しましょう。
また中線定理を覚えていると、計算が楽になる場面が多々あります。中線定理を利用できる場合、積極的に活用しましょう。
三角形の定理を覚えるのは重要です。外心や垂心、内心、重心が何を意味しているのか理解し、中線定理を含めてそれぞれの定理の性質を覚えましょう。






