半透膜を利用することによって生じる圧力を浸透圧といいます。溶媒に溶質を溶かすことによって、半透膜を通して溶媒が移動するのです。
浸透圧は多くの場面で利用されています。例えば料理では、食塩水を利用することによって成分の溶けだしを防ぐことができます。果実酒であれば、アルコールが果物に浸透するのは浸透圧による影響です。
それでは、浸透圧を計算するにはどうすればいいのでしょうか。浸透圧の公式を覚える必要はなく、気体の状態方程式を理解している場合、浸透圧の計算が可能です。
なお浸透圧を理解するとき、半透膜の役割やファントホッフの法則を学ばなければいけません。そこで、浸透圧の性質や特徴を解説していきます。
もくじ
浸透圧で重要な半透膜の役割
浸透圧を理解するためには、半透膜とは何かを学ばなければいけません。半透膜とは、特定の物質は通過できるものの、その他の物質は通過できない膜を指します。より詳しくいうと、水などの溶媒は半透膜を通過できるものの、溶質(塩化ナトリウムなど)は通過できません。
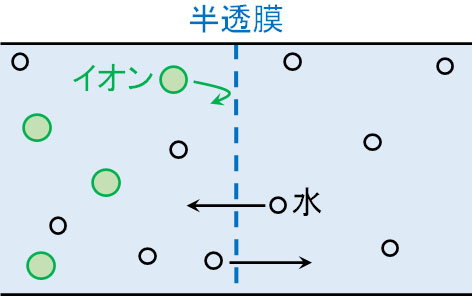
半透膜には非常に小さな穴が開いています。水など非常に小さい分子(溶媒)については、半透膜を通過できます。一方、イオンやグルコースなどの化合物は水よりもサイズが大きく、半透膜を通過できないのです(半透膜の穴の大きさによっては、イオンが通過できるケースもあります)。
浸透圧を生じるためには、半透膜を必ず利用しなければいけません。半透膜を利用することによって、溶媒が移動する圧力を生じるのです。
半透膜を通過する力(圧力)が浸透圧
それでは、半透膜を利用するとなぜ一方方向へ圧力を生じるようになるのでしょうか。まず、以下のように水のみが存在している状態では、浸透圧を生じません。
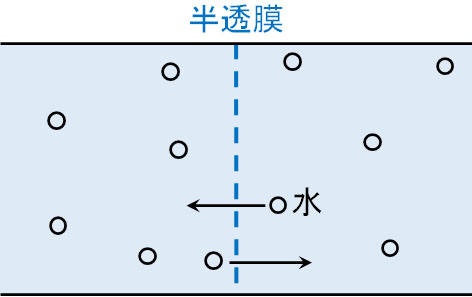
水は自由に半透膜を通過し、左側と右側を行き来することができます。当然、浸透圧は生まれません。
一方、片側に溶質(塩化ナトリウム、グルコースなど)が溶けている場合、浸透圧を生じます。例えばU字管を利用して真ん中を半透膜で区切り、左側に食塩水、右側に純水を入れます。そうすると、右側にある水分子は食塩水のほうへ移動します。
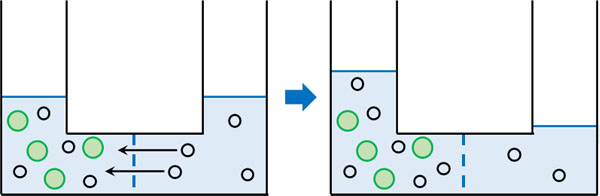
このとき、液面の高さを同じにするためには、左側に圧力をかけなければいけません。圧力をかけることによって両側の液面の高さが同じになる場合、このときの圧力を浸透圧といいます。
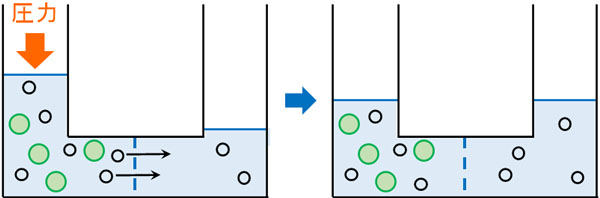
ただ、浸透圧の定義を厳密に利用する必要はありません。「左側と右側で溶質の濃度差を生じているとき、半透膜を通じて生じる圧力が浸透圧」と理解すれば十分です。
溶質を溶かすことで浸透圧を生じる理由
それでは、なぜ浸透圧を生じるのでしょうか。溶媒がどちらに動くのかについて、暗記しても意味がありません。どこに濃度差を生じているのかは提示される問題によって変わります。そこで覚えるのではなく、浸透圧を生じる原理を理解しましょう。原理を理解すれば、覚えなくても浸透圧の向きがわかります。
自然現象を理解するとき、重要なのは分子を可視化することです。実際には分子を見ることができないものの、分子を見ることができると仮定して自然現象を考えるのです。
それでは先ほどと同様に、半透膜で区切って左側に溶質を溶かし、右側に純水が存在している場面を考えましょう。水は自由に半透膜を通過できるため、右側から左側への移動はスムーズです。
一方、左側から右側への水の移動は困難です。左側には塩化ナトリウムやグルコースなどの溶質が溶けています。これらの粒子(溶質)はサイズが大きいため、半透膜の穴をふさぎます。
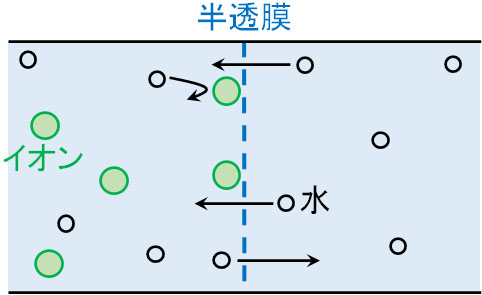
障害物がある場合、物理的に水は左側から右側へ移動することが難しいです。多少、水は左側から右側へ移動することはできるものの、障害物があるため、右側から左側へ移動する水の量のほうが多くなります。
その結果、右側から左側へ溶媒(水)が移動します。これが、浸透圧(溶媒が移動しようとする圧力)を生じる理由です。
・浸透圧は多くの場面で重要
なお、浸透圧による現象は多くの場面で応用されています。例えば、私たちの細胞は半透膜で構成されています。点滴をするとき、純水を私たちの血液に入れると、浸透圧によって細胞内の水は血管内へ流れ出るようになります。こうして、激しい痛みを生じます。
点滴で生理食塩水(体液と同じ浸透圧の食塩水)を利用しているのは、浸透圧を考慮しているからなのです。
また私たちが果実酒を作るとき、アルコールに果実を入れます。果実には多くの成分が含まれている一方、アルコールは溶媒(エタノール)です。そのためアルコールが果物の中へ浸透していき、熟成されます。浸透圧というのは、私たちの生活で重要な自然現象なのです。
ファントホッフの法則を利用する浸透圧の公式
次に、浸透圧を計算できるようになりましょう。浸透圧をπ(Pa)、水溶液の体積をV(L)、物質量をn(mol)、気体定数をR(Pa·L/(K·mol))、温度をT(K)とすると、浸透圧を得る公式は以下になります。
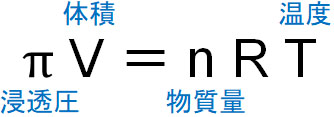
この関係をファントホッフの法則といいます。ファントホッフの法則とは、「上記の公式によって浸透圧を得られること」であると理解しましょう。
なお、化学を学んでいる人であれば、この公式を既に知っています。より詳しくいうと、気体の状態方程式とまったく同じ公式であると気づきます。
気体の状態方程式では、圧力P(Pa)を利用します。そこで圧力Pではなく、浸透圧π(Pa)に変えましょう。両方とも単位はPaであり、Pをπに変換することでファントホッフの法則を得ることができます。そのため、浸透圧の公式を新たに覚える必要はありません。
・電離する化合物は物質量が増加する
なお浸透圧を計算するとき、気体の圧力を計算するときとは異なり、化合物が電離するかどうかを確認しましょう。気体では、化合物は電離しません。一方、溶媒に溶けることによって電離する化合物はたくさんあります。
ファントホッフの法則で利用される物質量というのは、溶液中に溶けている粒子の物質量を表します。
例えば1molのNaClを溶かす場合、合計で2mol(1molのNa+と1molのCl–)のイオンが生成されます。つまり、物質量は2倍になります。これはつまり、1molの塩化ナトリウムを溶かす場合、浸透圧の計算では2molの物質が存在していると考えて計算しなければいけないことを意味しています。
またCaCl2を1mol溶かす場合、合計で3mol(1molのCa2+と2molのCl–)が生成されます。つまり、物質量は3倍になります。気体とは異なり、化合物が溶ける場合、粒子の物質量が増加するケースがあることに注意しましょう。
公式を利用して浸透圧を計算する
それでは、実際に浸透圧を計算してみましょう。公式は気体の状態方程式と同じなので、浸透圧の計算は難しくありません。公式に値を代入することで答えを得ましょう。
例えば、以下の問題の答えは何でしょうか。
- 1.17gのNaClを830mLの水に溶かし、半透膜で区切った管に入れました。27℃のとき、溶液の浸透圧は何Paでしょうか。なおNaClの式量を58.5、気体定数Rを8.3×103(Pa·L/(K·mol))とします。
まず、物質量はいくらでしょうか。NaClの式量は58.5であるため、以下のように計算しましょう。
\(\displaystyle\frac{1.17}{58.5}=0.02\)
NaClの物質量は0.02molです。ただ塩化ナトリウムは水溶液中で電離し、Na+とCl–になります。粒子の数が2倍になるため、浸透圧の計算では0.04molを利用しましょう。
また水溶液の体積0.83L、物質量0.04mol、気体定数8.3×103、温度300Kを公式に当てはめると、以下のように答えを得ることができます。
\(0.83π=0.04×8.3×10^3×300\)
\(π=1.2×10^5\)
こうして、浸透圧は1.2×105Paと計算することができました。
公式を変形し、質量や分子量、モル濃度を利用する
なお気体の状態方程式では、公式を変形することで質量や分子量を用いた式へと変形することができます。ファントホッフの法則は気体の状態方程式とまったく同じであるため、当然ながら同様に質量や分子量を用いた式へ変形できます。
物質量n(mol)というのは、溶質の質量w(g)と分子量Mを用いて\(\displaystyle\frac{w}{M}\)と表すことができます。物質量の計算は化学の基本であるため、これについては問題なく理解できると思います。
そこで、物質量nを\(\displaystyle\frac{w}{M}\)へ変換しましょう。

また浸透圧の計算では、モル濃度C(mol/L)を利用して計算することもあります。物質量n(mol)を溶媒の体積V(L)で割れば、モル濃度を得ることができます。そこで、以下のように公式を変形しましょう。
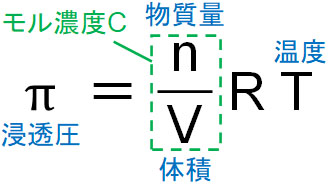
これらの公式を覚える必要はありません。浸透圧の公式(ファントホッフの法則)を利用して、そのつど式を作れるようになりましょう。
浸透圧の公式を変形し、答えを得る
それでは、実際に公式である\(πV=nRT\)を変形して、浸透圧の問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 体温が37℃のとき、人の血液の浸透圧は7.5×105Paです。血液中の溶質のモル濃度(mol/L)はいくらでしょうか。なお、気体定数Rは8.3×103(Pa·L/(K·mol))です。
わからない値はモル濃度(mol/L)です。そこで単位に着目すると、物質量n(mol)に対して溶媒の体積V(L)で割ればいいとわかります。つまり、公式を以下のように変形する必要があります。
\(πV=nRT\)
\(\displaystyle\frac{π}{RT}=\displaystyle\frac{n}{V}\)
\(\displaystyle\frac{n}{V}\)がモル濃度であるため、\(\displaystyle\frac{π}{RT}\)を計算すれば答えを得ることができます。
\(\displaystyle\frac{n}{V}=\displaystyle\frac{7.5×10^5}{8.3×10^3×310}\)
\(\displaystyle\frac{n}{V}≒0.29\)
こうして、0.29mol/Lが答えであるとわかります。
浸透圧は重要な自然現象の一つ
最も身近な自然現象の一つが浸透圧です。料理をするとき、お酒を造るとき、医療サービスを受けるとき、あらゆる場面で浸透圧が利用されています。
半透膜を利用することによって浸透圧を生じるようになります。溶媒に溶質が溶けることによって、浸透圧が生まれるのです。そこで、なぜ溶液の濃さに違いがあると浸透圧を生じるのか理解しましょう。原理を学べば、溶媒がどの方向に移動するのかわかります。
またファントホッフの法則を利用して浸透圧を計算しましょう。それに加えて、公式を変形して質量や物質量、モル濃度を利用した計算を行えるようになりましょう。
浸透圧を得る公式は気体の状態方程式と同じなので、新たな公式を覚える必要はありません。そこで浸透圧を生じる原理を学び、公式を利用できるようになるといいです。






