高校数学では微分を学びます。微分を利用することによって、接線の傾きを知ることができます。それでは、接線の方程式はどのように計算すればいいのでしょうか。微分によって傾きを得た後、公式を利用すると接線の方程式を簡単に得ることができます。
また接線に対して、垂直(90°)に交わる線を法線といいます。接線の方程式を求めることができる場合、法線の方程式を得ることができます。
なおこれら接線や法線の方程式を計算できる場合、より複雑な計算を行えるようにしましょう。2つの曲線に接する線を求めたり、2曲線が接する場合の接線を計算したりするのです。
微分を利用することによって、方程式を計算できるようになります。そこで、どのように接線や法線を出せばいいのか解説していきます。
もくじ
接線の方程式を得るとき、微分を利用して傾きを計算する
微分することによって、接線の傾きを得ることができます。そのため接線の方程式を得たい場合、まずは微分しましょう。
例えば、以下の関数について座標\((2,16)\)の接線の傾きは何でしょうか。
- \(y=2x^3\)
接線の方程式を得るため、微分すると以下のようになります。
- \(y’=6x^2\)
そのため\(x\)座標が2のとき、\(6×2^2=24\)であるため、接線の傾きは24であるとわかります。
座標がわかっている場合の方程式
ただ接線の傾きがわかっても、直線の方程式を得ることはできません。一次関数は\(y=ax+b\)で表されるため、\(b\)の値を知る必要があります。
そこで、座標を利用して方程式を出しましょう。傾きは既にわかっているため、方程式は\(y=24x+b\)です。またこの方程式は座標\((2,16)\)を通るため、\(y=24x+b\)に代入しましょう。以下のようになります。
- \(16=24×2+b\)
次に、\(y=24x+b\)から\(16=24×2+b\)を引きましょう。以下の連立方程式を作るのです。
\(\begin{eqnarray} \left\{\begin{array}{l}y=24x+b\\16=24×2+b\end{array}\right.\end{eqnarray}\)
こうして、以下の式を作ることができます。
\(y-16=24(x-2)\)
この式を計算すると、\(y=24x-32\)が答えであるとわかります。つまり\((2,16)\)を通り、傾きが24の直線になります。
なお先ほど計算したり方程式を確認すると、接線を出すための公式を導くことができます。\(x\)座標が\(a\)の場合、接線の傾きは\(f'(a)\)です。また座標は\((a,f(a))\)なので、接線の公式は以下のようになります。
- \(y-f(a)=f'(a)×(x-a)\)

この公式を利用すれば、連立方程式を利用せずに答えを出すことができます。傾きが24であり、座標\((2,16)\)を通るのであれば、公式に代入することで\(y-16=24(x-2)\)の式を作ることができます。
傾きのみわかっている場合の方程式の出し方
次に、傾きのみわかっているときの一次方程式の出し方を学びましょう。つまり、接点がわかっていないケースです。
例えば、以下の問題の答えは何でしょうか。
- \(y=x^3\)について、傾きが3のときの方程式を求めましょう。
まずは微分しましょう。以下のようになります。
\(y’=3x^2\)
接点の\(x\)座標を\(a\)とすると、接線の傾きは\(3a^2\)とわかります。また傾きは3とわかっているため、以下の式を作ることができます。
\(3a^2=3\)
\(a^2=1\)
\(a=-1,1\)
こうして\(a=-1\)または\(a=1\)のとき、傾きが3になるとわかります。つまり\((-1,-1)\)と\((1,1)\)の座標について、接線を引くと傾きが3の一次方程式を得られます。イメージは以下のようになります。
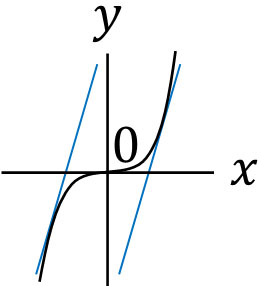
そこで、傾きが3で\((-1,-1)\)または\((1,1)\)を通る直線の方程式を計算しましょう。以下のようになります。
・接点\((-1,-1)\)を通る直線
接線の公式に代入すると
\(y+1=3(x+1)\)
\(y=3x+2\)
・接点\((1,1)\)を通る直線
接線の公式に代入すると
\(y-1=3(x-1)\)
\(y=3x-2\)
こうして、答えを出すことができます。
曲線上にない点を通る場合の答え
それでは、曲線上にない点を通る場合はどのように計算すればいいのでしょうか。この場合、先ほど解説した\(y-f(a)\)\(=f'(a)×(x-a)\)の公式を利用して答えを出しましょう。
例えば、以下の問題の答えは何でしょうか。
- \(y=x^3-5x^2+4x\)に接し、原点を通る直線の方程式を求めましょう。
イメージは以下のようになります。

このように、グラフ上ではない点を通ります。また今回の問題では、直線は原点\((0,0)\)を通ります。なお傾きを出す必要があるため、まずは微分しましょう。以下のようになります。
\(y’=3x^2-10x+4\)
こうして、点\((a,f(a))\)での接線の傾きは\(3a^2-10a+4\)であるとわかります。また\(x\)座標が\(a\)のとき、\(y\)は\(f(a)=a^3-5a^2+4a\)です。そこで、先ほどの公式を利用して以下の式を作りましょう。
\(y-(a^3-5a^2+4a)\)\(=(3a^2-10a+4)(x-a)\)
\(y-a^3+5a^2-4a\)\(=(3a^2-10a+4)x\)\(-3a^3+10a^2-4a\)
\(y=(3a^2-10a+4)x-2a^3+5a^2\)
こうして、点\(a\)を通る一次方程式がわかります。また原点を通るため、直線は\((0,0)\)を通ります。そのため、\(x=0,y=0\)を代入することで以下の式を作れます。
\(-2a^3+5a^2=0\)
この式を解きましょう。以下のようになります。
\(-2a^3+5a^2=0\)
\(-a^2(2a-5)=0\)
こうして、\(a=0\)または\(a=\displaystyle\frac{5}{2}\)になります。
そこで\(y=(3a^2-10a+4)x\)\(-2a^3+5a^2\)について、\(a=0\)と\(a=\displaystyle\frac{5}{2}\)を代入しましょう。
・\(a=0\)のとき
\(y=4x\)
・\(a=\displaystyle\frac{5}{2}\)のとき
\(y=\{3×\left(\displaystyle\frac{5}{2}\right)^2-10×\left(\displaystyle\frac{5}{2}\right)+4\}x+0\)
\(y=(\displaystyle\frac{75}{4}-25+4)x\)
\(y=-\displaystyle\frac{9}{4}x\)
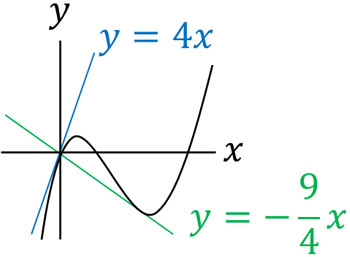
こうして、答えを得ることができます。点\((a,f(a))\)の接線について、公式を利用して方程式を作りましょう。またこの方程式が特定の点を通る場合、その座標を代入しましょう。そうすると、直線の方程式を出すことができます。
法線の方程式を求める方法
なお微分を利用して一次方程式をだす場合、法線の方程式を問われることがあります。法線とは、直線に対して直角に交わる線を指します。接線に対して、法線は以下のようになります。
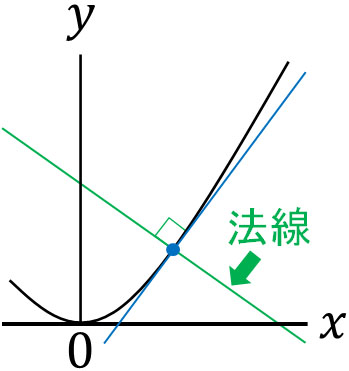
それでは、直角に交わる直線を計算するにはどうすればいいのでしょうか。このとき直角に交わる一次方程式について、「接線と法線の傾きをかけると必ず-1になる」という性質があります。
例えば法線の傾きを\(a\)とする場合、\(y=2x\)に対する法線の傾きは\(2×a=-1\)で計算できます。つまり、法線の傾きは\(a=-\displaystyle\frac{1}{2}\)です。
また\(y=5x\)に対する法線の傾きは\(5×a=-1\)で計算できます。つまり、法線の傾きは\(a=-\displaystyle\frac{1}{5}\)です。このように、直角に交わる直線の傾きをかけると必ず-1になる性質を覚えましょう。そうすると、法線が関わる問題を解けるようになります。
例えば、以下の問題の答えは何でしょうか。
- \(y=x^3+x\)について、点\((1,2)\)を通る法線の方程式を求めましょう。
接線の方程式を計算する方法は既に解説しました。ただ接線ではなく、法線を求めなければいけません。法線の傾きを得るため、微分しましょう。以下のようになります。
\(y=3x^2+1\)
\(x=1\)のとき、接線の傾きは\(3×1^2+1=4\)です。そのため、法線の傾きは\(-\displaystyle\frac{1}{4}\)です。
傾きがわかれば、法線の方程式を得ることができます。点\((a,f(a))\)を通る接線の傾きについて、以下の公式を利用することで得られることを説明しました。
- \(y-f(a)=f'(a)×(x-a)\)
つまり傾きと接点の座標がわかれば、公式に代入することで一次方程式を得ることができます。ただ接線ではなく、法線の方程式を出さなければいけません。そこで接線の傾きではなく、法線の傾きを利用しましょう。
法線の傾きは\(-\displaystyle\frac{1}{4}\)であり、点\((1,2)\)を通るため、以下の式を作ることができます。
\(y-2=-\displaystyle\frac{1}{4}(x-1)\)
\(y=-\displaystyle\frac{1}{4}x+\displaystyle\frac{9}{4}\)
接線の一次方程式を得る公式を利用することによって、法線の方程式を得ることができます。接線の傾きではなく、法線の傾きを代入した後、接点の座標を代入しましょう。そうすると、法線の一次方程式を計算できます。
なお前述の通り、接線の傾きと法線の傾きをかけると-1になります。そのため、法線の傾きは\(-\displaystyle\frac{1}{f'(a)}\)です。つまり、接点の\(x\)座標が\(a\)の場合、法線の方程式は以下の公式によって求めることができます。
- \(y-f(a)=-\displaystyle\frac{1}{f'(a)}×(x-a)\)
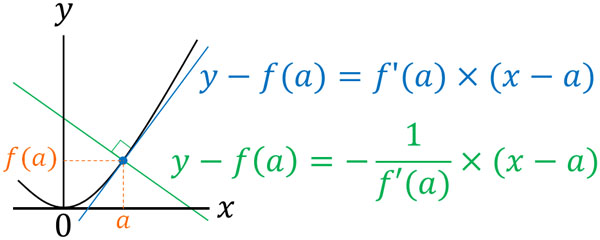
ただ、この公式を覚える必要はありません。接線の方程式を出す公式を理解していれば、公式を変形することで法線の方程式を出す公式に変えることができるからです。
直線が2つの曲線に接する場合の解答
次に、発展的な問題を解けるようになりましょう。直線(一次方程式)が2つの曲線に接するとき、接線の方程式を求めるようにするのです。以下のイメージです。
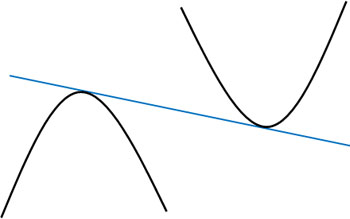
接線の方程式を出す必要があるため、微分しなければいけないことがわかります。それでは、以下の問題の答えは何でしょうか。
- \(y=x^2-6x+5\)と\(y=-x^2\)の関数について、共通する接線の方程式を求めましょう。
まず、\(y=-x^2\)を微分しましょう。以下のようになります。
- \(y’=-2x\)
\(y=-x^2\)の関数について、接点の\(x\)座標を\(a\)とすると、接点は\((a,-a^2)\)になります。傾き(\(-2a\))と接点がわかるため、\(y=-x^2\)の接線を計算できます。以下のようになります。
\(y-(-a^2)=-2a(x-a)\)
\(y+a^2=-2ax+2a^2\)
\(y=-2ax+a^2\)
こうして、\(y=-x^2\)の接線が\(y=-2ax+a^2\)になるとわかりました。また、\(y=-2ax+a^2\)は\(y=x^2-6x+5\)とも接します。2つの関数が接するため、\(y\)の値が同じになる点をもちます。そのため、以下の式を作ることができます。
\(-2ax+a^2=x^2-6x+5\)
\(x^2+(2a-6)x+5-a^2=0\)
また2つの関数が接する条件として、二次関数が重解をもたなければいけません。つまり、判別式がゼロ(\(D=0\))になる必要があります。
\(D=b^2-4ac\)
代入すると、
\((2a-6)^2-4×1×(5-a^2)=0\)
\((4a^2-24a+36)-20+4a^2=0\)
\(8a^2-24a+16=0\)
\(8(a^2-3a+2)=0\)
\(8(a-1)(a-2)=0\)
こうして、\(a=1\)または\(a=2\)のとき、接線\(y=-2ax+a^2\)は\(y=x^2-6x+5\)とも接する(重解をもつ)ようになります。そこで、\(a=1\)と\(a=2\)を\(y=-2ax+a^2\)に代入しましょう。そうすると、以下の答えを得ることができます。
- \(y=-2x+1\)
- \(y=-4x+4\)
こうして、\(y=x^2-6x+5\)と\(y=-x^2\)に接する一次方程式を得ることができます。参考までに、以下のようなイメージになります。
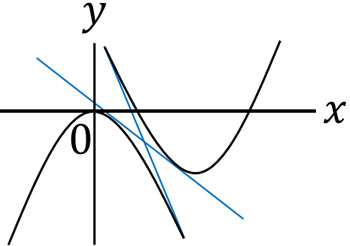
今回の問題について、別の方法を利用して解くこともできます。ただ微分を利用すれば直線の方程式を得ることができるため、計算しやすくなります。
2つの曲線が接するとき、接線の方程式
次に、2つの曲線が互いに接するときの接線の方程式を計算できるようになりましょう。イメージは以下のようになります。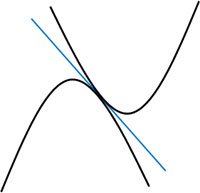
2つの関数を\(f(x)\)と\(g(x)\)とするとき、一つの点で接するので\(f(x)=g(x)\)となります。また接線の傾きは同じなので、\(f'(x)=g'(x)\)となります。この性質を利用して問題を解きましょう。
例えば、以下の問題の答えは何でしょうか。
- \(y=x^3-x^2-12x-1\)と\(y=-x^3+2x^2+a\)が接するとき、\(a\)の値と接線の方程式を求めましょう。
まず、2つの関数を微分しましょう。以下のようになります。
- \(y’=3x^2-2x-12\)
- \(y’=-3x^2+4x\)
接点の\(x\)座標を\(t\)としましょう。接点\(t\)について、接線の傾きは同じであるため、\(f'(t)=g'(t)\)となります。そのため、以下の式を作ることができます。
\(3t^2-2t-12=-3t^2+4t\)
\(6t^2-6t-12=0\)
\(6(t^2-t-2)=0\)
\(6(t+1)(t-2)=0\)
こうして\(t=-1\)または\(t=2\)のとき、\(f'(t)=g'(t)\)になるとわかります。
また一つの点で接するため、前述の通り\(f(t)=g(t)\)です。そのため、以下の式を作ることができます。
\(t^3-t^2-12t-1=-t^3+2t^2+a\)
\(a=2t^3-3t^2-12t-1\)
・\(t=-1\)のとき
\(a=-2-3+12-1=6\)
\(t=-1\)のとき、接線の傾きは\(f'(-1)=-7\)です。また\(f(-1)=9\)であるため、接点の座標は\((-1,9)\)です。そのため、接線の方程式は以下になります。
\(y-9=-7(x+1)\)
\(y-9=-7x-7\)
\(y=-7x+2\)
\(a=6\)のとき2つの曲線は接し、接線の方程式は\(y=-7x+2\)です。
・\(t=2\)のとき
\(a=16-12-24-1=-21\)
\(t=2\)のとき、接線の傾きは\(f'(2)=-4\)です。また\(f(2)=-21\)であるため、接点の座標は\((2,-21)\)です。そのため、接線の方程式は以下になります。
\(y+21=-4(x-2)\)
\(y+21=-4x+8\)
\(y=-4x-13\)
\(a=-21\)のとき2つの曲線は接し、接線の方程式は\(y=-4x-13\)です。こうして、答えを出すことができます。
微分を利用し、接線の方程式を得る
接線の傾きを得るとき、微分は非常に有効です。一次方程式の傾きを利用する問題では、まずは微分することを考えましょう。
微分することによって傾きを得た後、公式を利用することで一次方程式を出すことができます。連立方程式によって直線の方程式を得ることはできるものの、公式を利用するほうが簡単に計算できます。
また傾きと座標を利用して方程式を得られるようになったあと、発展問題を解けるようになりましょう。2つの曲線に接する直線を求めたり、2つのグラフが接するときの接線を得たりするのです。
微分によって接線を得た後、方程式を計算できるようになりましょう。これによって、直線の式がわかるようになります。