関数を利用することにより、特定の値を得ることができます。このとき、関数には逆関数や合成関数があります。
逆関数と合成関数の概念は難しくありません。\(x\)と\(y\)の式を反対にすると逆関数になります。また、2つの関数を組み合わせると合成関数になります。そこで、関数を逆関数や合成関数へ変形できるようになりましょう。
なお、逆関数と合成関数は関係しています。合成関数の性質を学ぶとき、逆関数を利用するのです。そのため、逆関数と合成関数を同時に学ばなければいけません。
それでは、逆関数と合成関数を利用してどのように計算すればいいのでしょうか。逆関数と合成関数について解説していきます。
もくじ
\(y\)の値を決めると\(x\)の値が決まる逆関数
\(x\)の値が決まると、自動的に\(y\)の値が決まる場合、その式を関数といいます。例えば\(y=2x\)は関数であり、\(x\)の値が決まると\(y\)の値が決まります。
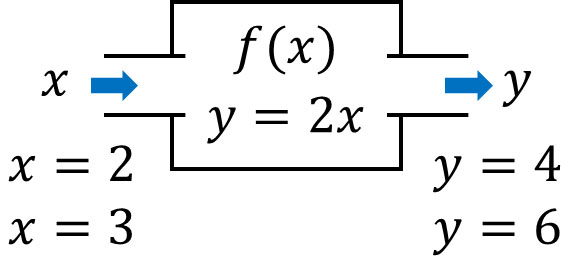
一方、例えば\(x^2+y^2=25\)は関数ではありません。\(x=3\)の場合、\(y=±4\)であり、一つの答えを得られるわけではありません。\(x\)の値が決まると、\(y\)の値が一つだけ決まるのが関数の条件です。
先ほどの例が円関数ではなく、円の方程式と呼ばれているのは、一つの\(x\)と一つの\(y\)が対応していないからなのです。
なお関数では一つの値が明確に決まるため、反対の場合についてもいえます。つまり、\(y\)の値を決めると\(x\)の値が決まります。これを逆関数といいます。関数である場合、逆関数も成り立つケースが多いのです。
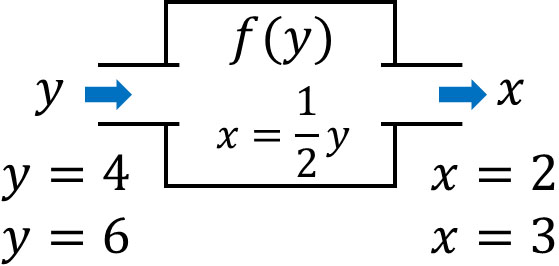
関数\(f(x)\)に対して、逆関数を\(f^{-1}(x)\)と表します。
逆関数を作る方法と条件
それでは、逆関数を作れるようになりましょう。考え方は簡単であり、\(y=…\)の式を\(x=…\)の式へ変形すればいいです。その後、\(x\)と\(y\)を入れ替えましょう。以下の問題の答えは何でしょうか。
- \(y=2x+4\)の逆関数を求めましょう。
以下のように式を変形しましょう。
\(y=2x+4\)
\(2x=y-4\)
\(x=\displaystyle\frac{y}{2}-2\)
次に、\(x\)と\(y\)を入れ替えると\(y=\displaystyle\frac{x}{2}-2\)となります。こうして、逆関数を作ることができました。
なお、すべての関数で逆関数を作れるとは限りません。例えば\(y=x^2\)について、\(x\)の値が決まると\(y\)の値も決まります。ただ、\(y\)の値が決まっても候補となる\(x\)の値は二つ存在するため、一つに決めることができません。この場合、逆関数を作れません。
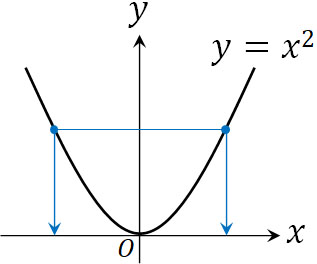
ただし、\(y=x^2\)について\(x\)の範囲を\(x≧0\)に限定する場合、逆関数を作ることができます。
直線\(y=x\)に対称となる逆関数のグラフ
なお、関数と逆関数には「直線\(y=x\)に対して対称になる」という性質があります。先ほど、\(y=2x+4\)の逆関数が\(x=\displaystyle\frac{y}{2}-2\)と解説しました。そこで、以下のように図を作りましょう。
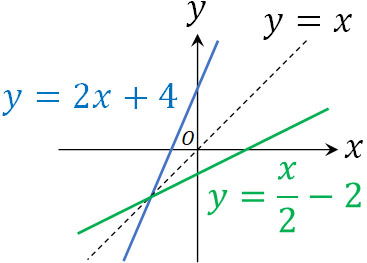
このように確認すると、直線\(y=x\)に対して対称とわかります。
参考までに、指数関数と対数関数は逆関数の関係にあります。例えば、\(y=2^x\)を逆関数にしましょう。
\(y=2^x\)
\(log_2y=log_22^x\)
\(x=log_2y\)
\(x\)と\(y\)を入れ替えると\(y=log_2x\)となります。グラフにすると以下になります。
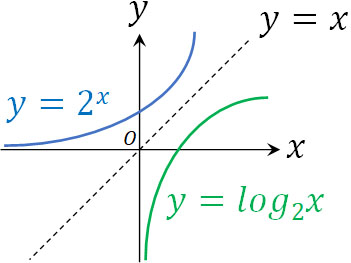
このように、直線\(y=x\)に対して対称となっています。なお\(y=2^x\)では必ず\(y>0\)になります。一方、逆関数である\(y=log_2x\)では必ず\(x>0\)になります。このように、領域についても\(x\)と\(y\)が入れ替わっています。
直線\(y=x\)に対して対称というのは、図形の形だけでなく、領域も\(x\)と\(y\)が入れ替わることを理解しましょう。
2つの関数を組み合わせる合成関数
次に合成関数を学びましょう。合成関数の計算は簡単であり、一つの関数をほかの関数へ代入すればいいです。例えば\(f(x)=x^2\)であり、\(g(x)=x+1\)のとき、合成関数\((f \circ g)(x)\)を以下のように表すことができます。
\((f \circ g)(x)=f(g(x))\)
\(=(x+1)^2\)
このように\(f(x)=x^2\)について、\(x\)へ\(g(x)=x+1\)を代入することで合成関数を得ることができます。
例えば\(y=2^{3x+1}\)というのは、\(f(x)=2^x\)と\(g(x)=3x+1\)を組み合わせ、\((f \circ g)(x)=2^{3x+1}\)にした関数と考えることができます。代入するだけなので、合成関数の概念は簡単です。
合成関数の性質:交換法則と結合法則
それでは、合成関数にはどのような性質があるのでしょうか。合成関数について、以下の性質を学びましょう。
- 交換法則は一般的に成り立たない:\((f \circ g)(x)≠(g \circ f)(x)\)
- 結合法則は成り立つ:\(((f \circ g) \circ h)(x)=(f \circ (g \circ h))(x)\)
例えば\(f(x)=x^2\)、\(g(x)=x+1\)について、以下のようになります。
- \((f \circ g)(x)=(x+1)^2\)
- \((g \circ f)(x)=x^2+1\)
このように、順番を変えると異なる関数になります。これが、一般的に交換法則が成り立たない理由です。
一方で結合法則は成り立ちます。例えば\(f(x)=x^2\)、\(g(x)=x+1\)、\(h(x)=x+2\)について、以下のようになります。
- \((f \circ g)(x)=(x+1)^2\)であるため、\(((f \circ g) \circ h)(x)=(x+3)^2\)
- \((g \circ h)(x)=x+3\)であるため、\((f \circ (g \circ h))(x)=(x+3)^2\)
このように、\(((f \circ g) \circ h)(x)\)\(=(f \circ (g \circ h))(x)\)となります。
逆関数と合成関数の関係
ここまで、逆関数と合成関数を学んできました。それでは、逆関数と合成関数の関係性を学びましょう。例として、\(f(x)=2x+4\)を利用します。この関数の逆関数は先ほど計算した通り\(f^{-1}(x)=\displaystyle\frac{x}{2}-2\)です。
そこで、\((f \circ f^{-1})(x)\)を計算しましょう。
\((f \circ f^{-1})(x)=2×\left(\displaystyle\frac{x}{2}-2\right)+4\)
\((f \circ f^{-1})(x)=x\)
次に、\((f^{-1} \circ f)(x)\)を計算しましょう。
\((f^{-1} \circ f)(x)=\displaystyle\frac{2x+4}{2}-2\)
\((f^{-1} \circ f)(x)=x\)
こうして、\((f \circ f^{-1})(x)\)\(=(f^{-1} \circ f)(x)=x\)になるとわかります。逆関数と合成関数には関係性があるのです。
逆関数と合成関数の性質を学ぶ
数学で必ず学ぶ内容が関数であり、逆関数と合成関数の概念を理解しましょう。逆関数と合成関数の概念は簡単であり、容易に逆関数や合成関数を作ることができます。
逆関数を作るとき、\(x=…\)の式へ変形した後、\(x\)と\(y\)を交換しましょう。これにより、直線\(y=x\)に対して対称な式を得ることができます。\(x\)や\(y\)に範囲がある場合、領域についても\(x\)と\(y\)が入れ替わります。
また合成関数を作るとき、一つの関数を一方の関数に代入しましょう。合成関数では交換法則は成り立たないものの、結合法則は成り立ちます。逆関数を利用して合成関数を作ると、必ず答えが\(x\)になるのも特徴です。
逆関数と合成関数は数学で基本的な内容の一つであり、微分や積分を学ぶときにも役立ちます。そこで、逆関数と合成関数の基本を理解しましょう。






