特定の規則性をもつ数を一列に並べる場合、それを数列といいます。数列で最も基本的な内容が等差数列であり、足し算または引き算を利用して規則性を見つけることになります。
規則性を見つけることができれば、等差数列の公式を利用することによって答えを得ればいいです。公式は必ず覚える必要があるものの、等差数列の公式は難しくありません。なお等差数列を学ぶとき、等差中項や調和数列についても理解しましょう。
また等差数列では、すべての数を足す場合についても計算できるようになる必要があります。等差数列の和にも公式があり、利用できるようになりましょう。
それでは、等差数列の公式には何があるのでしょうか。また、どのように等差数列を計算すればいいのでしょうか。等差数列を利用して計算する方法を解説していきます。
もくじ
等差数列の定義と一般項
特定の規則性をもつ数字の羅列を数列といいます。例えば以下の場合、1から始まり、3ずつ増えていきます。
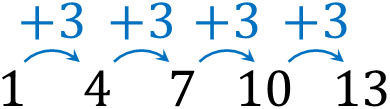
最初の数を初項、足す数を公差といいます。先ほどの数列の場合、初項1、公差3の等差数列になります。また1や4、7など、それぞれの数を項といいます。先ほどの数列では初項(第一項)が1、第二項が4、第三項が7です。
そこで、数列を文字で表しましょう。初項\(a\)、公差\(d\)の等差数列\(\{a_n\}\)について、第\(n\)項の一般項\(a_n\)を以下のように表すことができます。
- \(a_n=a+(n-1)d\)
等差数列では、項が一つ増えるごとに公差\(d\)が加わります。
- \(a_1=a\)
- \(a_2=a+d\)
- \(a_3=a+2d\)
- \(a_4=a+3d\)
- \(…\)
この条件を一般化すると、\(a_n=a+(n-1)d\)になるというわけです。例えば初項1、公差3の等差数列の一般項は以下になります。
\(a_n=1+(n-1)3\)
\(a_n=3n-2\)
初項(\(n=1\))の場合、\(n=1\)を代入すると\(a_1=1\)です。また第二項(\(n=2\))の場合、\(n=2\)を代入すると\(a_2=4\)です。第三項や第四項についても、先ほどの数列と値が一致します。こうして、等差数列の一般項を計算できます。
それでは、以下の問題の答えは何でしょうか。
- 第5項が\(12\)、第12項が\(-2\)の場合、等差数列の一般項を求めましょう。
初項を\(a\)、公差を\(d\)として以下のように式を作りましょう。
- 第5項:\(a+4d=12\)
- 第12項:\(a+11d=-2\)
そこで、連立方程式を解くと\(d=-2\)、\(a=20\)とわかります。そのため、一般項は\(a_n=20-2(n-1)\)\(=22-2n\)とわかります。
等差中項:等差数列の真ん中の一般項
等差数列には規則性があるものの、必ずしも初項を利用して計算するとは限りません。そこで、等差数列の性質を利用して数を計算できるようになりましょう。
3つの数が等差数列として並んでいる場合、中央の項を等差中項といいます。また等差中項を\(a\)、公差を\(d\)とすると、以下のような関係になります。
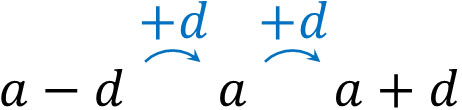
この場合、3つの項を足すと\(3a\)になります。例えば等差数列となっている3つの数があり、3つの数を足して36になる場合、中央の数は12とわかります。\(3a=36\)だからです。
また、等差数列となっている\(p,q,r\)の数があるとします。この場合、等差中項を利用すると以下の関係が成り立ちます。
- \(2q=q+r\)
\(q\)は等差中項です。また\(p=a-d\)、\(q=a\)、\(r=a+d\)であるため、\(2q=q+r\)に代入すると式が成り立つとわかります。等差中項では、これらの性質を利用しましょう。それでは、以下の問題の答えは何でしょうか。
- \(2,a,b\)がこの順番で等差数列を形成しており、3つの数を足して12になる場合、\(a\)と\(b\)を求めましょう。
この問題では\(a\)が等差中項です。等差中項の性質を利用すると、\(3a=12\)です。そのため、\(a=4\)です。また、以下の式が成り立ちます。
\(2a=2+b\)
\(8=2+b\)
\(b=6\)
こうして\(a=4\)、\(b=6\)とわかりました。
調和数列:逆数が等差数列となる計算
なお等差数列の中でも、特殊な数列に調和数列があります。逆数にすることで等差数列になる場合、調和数列といいます。調和数列が\(\{a_n\}\)の場合、\(\left\{\displaystyle\frac{1}{a_n}\right\}\)は等差数列になります。
- 調和数列:\(a_1,a_2,a_3…\)
- 等差数列:\(\displaystyle\frac{1}{a_1},\displaystyle\frac{1}{a_2},\displaystyle\frac{1}{a_3}…\)
言い換えると、逆数にすると等差数列になる場合、その数列を調和数列といいます。それでは、以下の問題の答えは何でしょうか。
- 第5項が\(\displaystyle\frac{1}{3}\)、第9項が\(\displaystyle\frac{1}{5}\)である調和数列の一般項\(a_n\)を求めましょう。
前述の通り、逆数を利用することで等差数列になる場合、調和数列といいます。そこで逆数をとると、第5項は3、第9項は5となります。そこで、以下の式を作りましょう。
- 第5項:\(a+4d=3\)
- 第9項:\(a+8d=5\)
そこで連立方程式を解くと、\(d=\displaystyle\frac{1}{2}\)、\(a=1\)となります。そのため、等差数列の一般項\(\displaystyle\frac{1}{a_n}\)は以下のようになります。
\(\displaystyle\frac{1}{a_n}=1+(n-1)·\displaystyle\frac{1}{2}\)
\(\displaystyle\frac{1}{a_n}=\displaystyle\frac{n+1}{2}\)
等差数列の一般項が\(\displaystyle\frac{n+1}{2}\)であるため、再び逆数を利用することで調和数列に戻しましょう。そのため、調和数列\(a_n\)の一般項は以下のようになります。
- \(a_n=\displaystyle\frac{2}{n+1}\)
こうして、調和数列の一般項を求めることができました。
等差数列の和の公式
ここまで、等差数列の一般項を求める公式や性質を解説してきました。なお、等差数列でひんぱんに出題される内容に等差数列の和があります。等差数列をすべて足すとき、等差数列の和\(S_n\)は以下のようになります。
- \(S_n=\displaystyle\frac{1}{2}n(a+l)\)
等差数列の和の公式は一つであり、この公式を必ず覚えるようにしましょう。
参考までに、2つの同じ等差数列を足し、2で割ることによって公式を得られます。ただ2つの等差数列を足すとき、一方は反対向きにします。初項\(a\)、末項\(l\)(最後の項)、公差\(d\)、項数\(n\)とすると、以下のようになります。
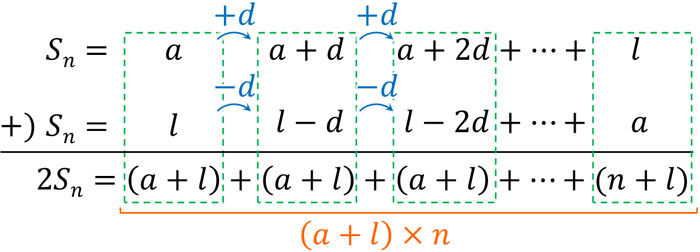
2つの同じ等差数列を足すことにより、\((a+l)\)を\(n\)個作ることができます。そのため、式は以下のようになります。
\(2S_n=n(a+l)\)
\(S_n=\displaystyle\frac{1}{2}n(a+l)\)
こうして、等差数列の和の公式を得ることができました。
ちなみに、公差\(d\)を利用して等差数列の和を計算することもできます。先ほど解説した等差数列の公式(一般項を得る公式)より、末項\(l\)は以下のように表すことができます。
- \(l=a+(n-1)d\)
そこで、\(l=a+(n-1)d\)を\(S_n=\displaystyle\frac{1}{2}n(a+l)\)に代入しましょう。
\(S_n=\displaystyle\frac{1}{2}n(a+l)\)
\(S_n=\displaystyle\frac{1}{2}n\{2a+(n-1)d\}\)
教科書には、\(S_n=\displaystyle\frac{1}{2}n\{2a+(n-1)d\}\)が公式として記されていることが多いです。ただこの公式を覚える必要はなく、\(S_n=\displaystyle\frac{1}{2}n(a+l)\)を利用して作れるようになりましょう。
それでは、以下の問題の答えは何でしょうか。
- 1~1000の整数について、7で割り切れる数をすべて足すといくらになるでしょうか。
7で割り切れる数というのは、言い換えると7の倍数です。つまり初項7、公差7の等差数列です。
- 7, 14, 21, 28, … , 994
なお\(994÷7=142\)であるため、994は第142項です。そこで、等差数列の和の公式を利用して計算しましょう。
\(S=\displaystyle\frac{1}{2}×142(7+994)\)
\(S=71071\)
こうして、答えは71071とわかりました。
条件を確認し、必要な部分の足し算・引き算を行う
なお等差数列の計算をするとき、条件によって必要な部分を足したり引いたりしましょう。例題として、以下の問題を解きましょう。
- 1~100までの整数のうち、2または3の倍数の和を求めましょう。
2の倍数については、初項2、末項100、項数50の等差数列です。そのため、以下のように計算できます。
\(S=\displaystyle\frac{1}{2}×50(2+100)\)
\(S=2550\)
また3の倍数については、初項3、末項99、項数33の等差数列です。そのため、以下のように計算できます。
\(S=\displaystyle\frac{1}{2}×33(3+99)\)
\(S=1683\)
ただ6の倍数の場合、2の倍数であり、かつ3の倍数でもあります。2の倍数の和と3の倍数の和を足すと、6の倍数の和が重なります。そこで、6の倍数の和を引きましょう。
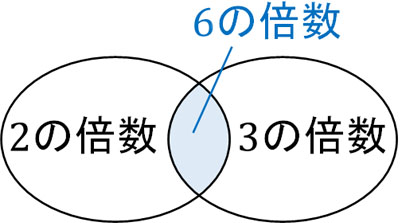
6の倍数については、初項6、末項96、項数16の等差数列です。
\(S=\displaystyle\frac{1}{2}×16(6+96)\)
\(S=816\)
そこで、以下のように足し算と引き算をしましょう。
\(2550+1683-816=3417\)
こうして、答えは3417とわかりました。
等差数列の和の最大
次に、等差数列の和の最大を計算できるようになりましょう。公差が負の数である場合、数は徐々に小さくなります。また、どこかの段階で数列に負の数が並ぶため、等差数列の和が小さくなります。
そこで等差数列の和を最大にするためには、数列で負の数になる前までを足すようにしましょう。それでは、以下の問題の答えは何でしょうか。
- 初項88、公差-6の等差数列について、初項から第\(n\)項までの和を\(S_n\)とするとき、\(S_n\)の最大値を求めましょう。
この数列では、以下のように6ずつ小さくなります。
- 88, 82, 76, 70…
そのため、数列で負の数になる前までを足せば最大になるとわかります。そうすると、\(88-6×(15-1)=4\)であるため、第15項(末項4)までを足せばいいとわかります。そこで、等差数列の和の公式を利用して計算しましょう。
\(S_1\)\(_5=\displaystyle\frac{1}{2}×15(88+4)\)
\(S_1\)\(_5=690\)
こうして、等差数列の和の最大値を得ることができました。
等差数列の公式を覚え、計算を行う
数列で最も基本的な内容が等差数列です。規則性のある数字の羅列が数列であり、等差数列では公差が同じです。
等差数列では、公式を利用して一般項を表すことができます。また等差数列の性質を利用すれば、等差中項や調和数列を利用することもできます。等差中項と調和数列は意味を理解していないと問題を解けないため、それぞれどのような数列なのか学びましょう。
なお等差数列で覚えなければいけない公式が等差数列の和です。等差数列の各項をすべて足すことにより、どのような値を得られるのか計算できるようになる必要があります。
数列で最初に学ぶ内容が等差数列です。数列が何を表しているのか理解して、規則性を見つけることで答えを得ましょう。