二次関数では下に凸、または上に凸のグラフになります。三次関数についても、デコボコのグラフとなります。
それでは、三次関数で\(y\)の値がどのように増減するのか調べるにはどうすればいいのでしょうか。これには微分を利用します。また微分することによって、極大値と極小値を求めることができます。
極大と極小の部分では、グラフの傾きはゼロになります。そのため、微分によって三次関数のグラフの形を調べることができるのです。
微分によって三次関数のグラフの形をどのように知るのかについて、解説していきます。
もくじ
微分によって三次関数の増減と極大・極小を調べる
傾きを知るために新たな関数を得る方法が微分です。微分することによって、傾きを得ることができます。
微分することによって関数\(f'(x)\)を得た後、\(f'(x)\)に値を代入することによって傾きがわかります。以下のように、\(f'(x)\)の値(傾き)がプラス、ゼロ、マイナスの場合、元の関数である\(f(x)\)は以下のようになります。
- \(f'(x)\)の値がプラス:\(f(x)\)は増加
- \(f'(x)\)の値がゼロ:\(f(x)\)の増加はゼロ
- \(f'(x)\)の値がマイナス:\(f(x)\)は減少
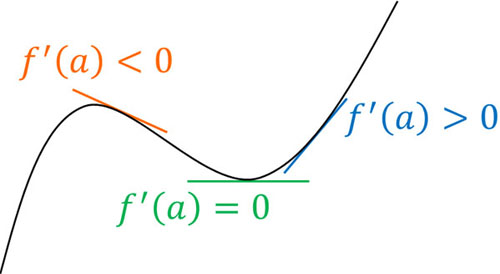
傾きがプラスであれば、\(f(x)\)が増加するのは当然です。また傾きがマイナスであれば、当然ながら\(f(x)\)は減少します。
なお三次関数のグラフを描くとき、重要な場所が\(f'(x)=0\)になる部分です。\(f'(x)=0\)の場合、傾きがゼロになります。傾きがプラスからマイナスになる場合、その部分を極大といいます。また傾きがマイナスからプラスに変わる場合、その部分を極小といいます。
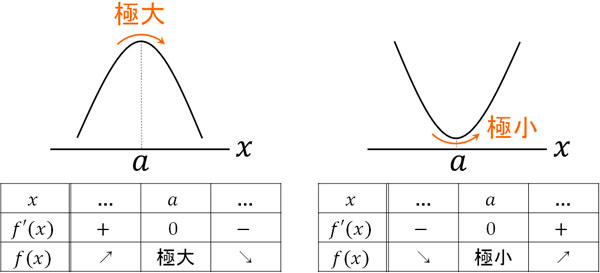
いずれにしても三次関数で増減を調べるとき、\(f'(x)=0\)に着目するようにしましょう。
極大値と極小値を見つけてグラフを描く
\(f'(x)=0\)で傾きがゼロになり、グラフの極大または極小が表れることを理解すれば、三次関数のグラフを描くことができます。
例えば、以下の三次関数のグラフはどのような形になるでしょうか。
- \(f(x)=x^3-\displaystyle\frac{9}{2}x^2+6x\)
三次関数のグラフを描くためには、まず微分しなければいけません。微分すると以下のようになります。
- \(f'(x)=3x^2-9x+6\)
次に因数分解することによって、\(f'(x)=0\)となる部分を探しましょう。
\(f'(x)=3x^2-9x+6\)
\(f'(x)=3(x^2-3x+2)\)
\(f'(x)=3(x-1)(x-2)\)
こうして\(x=1\)または\(x=2\)のとき、三次関数の傾きがゼロになるとわかります。次に、極大値\(f(1)\)と極小値\(f(2)\)を計算しましょう。以下のようになります。
\(f(1)=\displaystyle\frac{5}{2}\)
\(f(2)=8-18+12=2\)
そのため、以下のようなグラフを描くことができます。
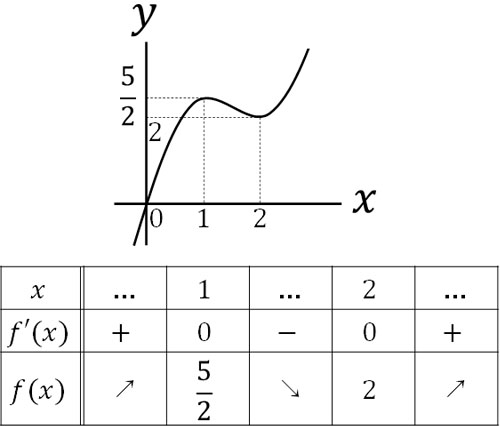
\(f(x)=x^3-\displaystyle\frac{9}{2}x^2+6x\)のグラフは原点を通ります。そこで原点を通り、\((1,\displaystyle\frac{5}{2})\)が極大値となり、\((2,2)\)が極小値となるグラフを描きましょう。そうすると、三次関数のグラフを描けるようになります。
極値をもたない三次関数のグラフの形
なお場合によっては、極値をもたない三次関数もあります。例えば、以下の三次関数のグラフの形はどのようになるでしょうか。
- \(f(x)=-\displaystyle\frac{1}{3}x^3+3x^2-9x+10\)
まずは微分してみましょう。以下のようになります。
- \(f'(x)=-x^2+6x-9\)
次に、\(f'(x)=0\)になる部分を調べるために因数分解しましょう。
\(f'(x)=-x^2+6x-9\)
\(f'(x)=-(x^2-6x+9)\)
\(f'(x)=-(x-3)^2\)
こうして、\(x=3\)のとき傾きがゼロになるとわかります。ただ\(f'(x)=0\)となる部分が一ヵ所のみです。そのため、この三次関数は極値をもちません。
なお、\(f(3)\)は以下のようになります。
\(f(3)=-9+27-27+10=1\)
また\(x=3\)以外、\(f'(x)<0\)です。そのため、グラフの形は以下になります。
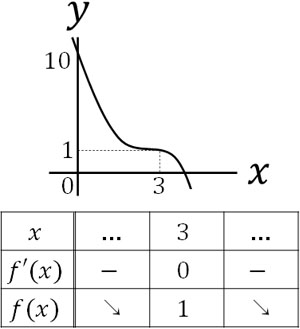
三次関数によっては、このように極値がないケースがあることを理解しましょう。
参考までに、三次関数のグラフを描けるようになれば、四次関数のグラフを描くことも可能です。微分することによって極大値と極小値の値を出し、グラフを描くのです。三次関数でも四次関数でも、グラフの描き方は同じです。
三次関数でのグラフの対称性
なお三次関数のグラフには対称性があります。つまり点対称となる場所があるのです。この事実を確かめてみましょう。
例として、以下の関数の対称性を確認しましょう。
- \(f(x)=x^3-6x^2+9x+2\)
この関数を微分すると、以下のようになります。
- \(f'(x)=3x^2-12x+9\)
次に極大値と極小値を調べるため、因数分解しましょう。
\(f'(x)=3x^2-12x+9\)
\(f'(x)=3(x^2-4x+3)\)
\(f'(x)=3(x-1)(x-3)\)
こうして、\(x=1\)のときに極大値、\(x=3\)のときに極小値になるとわかります。また、\(f(1)\)と\(f(3)\)の値は以下のようになります。
\(f(1)=1-6+9+2=6\)
\(f(3)=27-54+27+2=2\)
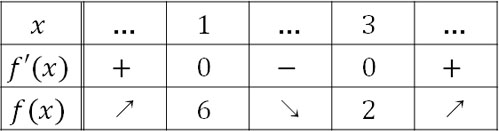
三次関数に対称性がある場合、極大値と極小値の中点は三次関数上になければいけません。そこで、極大値と極小値の中点を調べましょう。
極大値の座標は\((1,6)\)であり、極小値の座標は\((3,2)\)です。そのため、極大値と極小値の中点をMとすると、Mの座標は\((2,4)\)です。
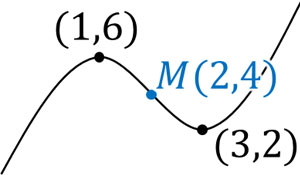
次に、三次関数\(y=f(x)\)はMに対して点対称であることを示しましょう。
\(y=f(x)\)上にある座標は\((x,y)\)と表すことができます。また座標M\((2,4)\)について、座標\((x,y)\)と対称な点の座標を\((A,B)\)とすると、以下のように表すことができます。
- \(\displaystyle\frac{x+A}{2}=2\)
- \(\displaystyle\frac{y+B}{2}=4\)

そのため、以下のように表すことができます。
- \(x=4-A\)
- \(y=8-B\)
そこで、\(y=x^3-6x^2+9x+2\)に代入しましょう。以下のようになります。
\(8-B=(4-A)^3-6(4-A)^2\)\(+9(4-A)\)\(+2\)
\(8-B=(64-48A+12A^2-A^3)\)\(-6(16-8A\)\(+A^2)\)\(-9A+38\)
\(8-B=-A^3+12A^2-57A+102\)\(+(-96+48A-6A^2)\)
\(8-B=-A^3+6A^2-9A+6\)
\(B=A^3-6A^2+9A+2\)
\(f(x)=x^3-6x^2+9x+2\)について、\(f(A)=B\)になるとわかります。つまり、点\((A,B)\)は\(f(x)\)上にあります。そのため、曲線\(y=f(x)\)は点Mに対して対称であり、三次関数は点対称となるポイントがあるとわかります。
数学の問題で三次関数の対称性を問われることがあります。このときは中点の性質を利用して、三次関数が点対称の性質をもつことを証明しましょう。
三次関数が極値をもつ条件:判別式の利用
ただすべての三次関数が極値をもつわけではありません。三次関数によっては、極大値や極小値をもたないことがあります。それでは、三次関数が極値をもつかどうかを見分けるにはどのようにすればいいのでしょうか。
三次関数を微分すると、二次関数を得ることができます。また\(f'(x)\)の二次関数について、\(f'(x)=0\)の解が2つある場合、三次関数の増減が変化します。つまり、極大値と極小値をもつとわかります。
一方、\(f'(x)=0\)の解が1つの場合、傾きが0になる部分はあるものの、極大値や極小値がありません。つまり、極値はありません。
\(f'(x)=0\)となる解が一つもない場合(虚数解)では、傾きが0になる部分がありません。つまりグラフは常に増加または減少をしていることになり、三次関数は極値をもちません。

つまり判別式を利用すれば、三次関数の形を判断できます。例えば、以下の問題の答えは何でしょうか。
- \(f(x)=x^3+ax^2+ax+1\)が極値をもつ\(a\)の値の範囲を求めましょう。
極値をもつかどうかは、微分することによって得られる関数につて、判別式を利用して判断します。そこで、まずは微分しましょう。以下のようになります。
- \(f'(x)=3x^2+2ax+a\)
次に、判別式(\(D\))を利用して解を2つもつ範囲を計算しましょう。以下のようになります。
\(D=b^2-4ac\)
代入すると、
\((2a)^2-4×3×a\)
\(4a^2-12a\)
つまり、\(4a^2-12a>0\)になれば2つの解をもつことになります。そこで、以下のように因数分解しましょう。
\(4a^2-12a>0\)
\(4a(a-3)>0\)
こうして、答えは\(a<0,3<a\)とわかります。\(a<0,3<a\)の場合、判別式(\(D\))は正の値になるため、傾きがゼロになる部分が2カ所あります。そのため、三次関数は極値をもつようになります。
三次関数の極大値と極小値の和または差では、解と係数の関係を利用する
なお場合によっては、三次関数の極大値と極小値について、和または差を求める問題が出されることがあります。極大値と極小値の座標について、足したり引いたりするのです。
この場合、極大値と極小値の値を計算するのは面倒です。そこで「三次関数の極大値と極小値を利用し、足し算や引き算をする問題」では解と係数の関係を利用しましょう。解と係数の関係についておさらいすると、二次関数の答えがαとβのとき、以下の性質があります。
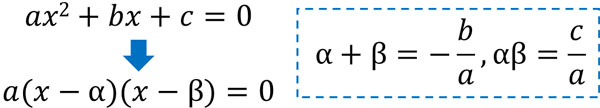
この性質を利用することによって答えを出しましょう。例えば、以下の問題の答えは何でしょうか。
- \(f(x)=x^3+ax^2+ax+1\)が\(x=α,β\)\((α<β)\)で極値をもつとき、\(f(α)+f(β)=2\)となる\(a\)の値を求めましょう。
極値をもつかどうかを確かめるとき、微分した後に得られる関数を確認しなければいけません。そこで、以下のように\(f(x)\)を微分しましょう。
- \(f'(x)=3x^2+2ax+a\)
またこの関数について、\(a<0,3<a\)のときに判別式(\(D\))が正の値になると先ほど計算しました。つまり、極値をもつためには\(a<0,3<a\)でなければいけません。
次に、解と係数の関係を利用しましょう。\(f'(x)=3x^2+2ax+a\)について、2つの答えを\(α,β\)とすると、以下の関係性となります。
- \(α+β=-\displaystyle\frac{2}{3}a\)
- \(αβ=\displaystyle\frac{1}{3}a\)
そこで、実際に\(f(α)+f(β)\)を計算してみましょう。\(f(x)=x^3+ax^2+ax+1\)に対して、\(x\)にαとβを代入し、足し算をするのです。
\(f(α)+f(β)\)
\(=α^3+aα^2+aα+1\)\(+β^3+aβ^2\)\(+aβ+1\)
\(=α^3+β^3+a(α^2+β^2)\)\(+a(α+β)\)\(+2\)
因数分解すると、以下のようになります。
\((α+β)^3\)\(-3αβ(α+β)\)\(+a(α+β)^2\)\(-2aαβ\)\(+a(α+β)\)\(+2\)
\(α+β=-\displaystyle\frac{2}{3}a\)であり、\(αβ=\displaystyle\frac{1}{3}a\)なので、因数分解した式に代入しましょう。
\(\left(-\displaystyle\frac{2}{3}a\right)^3\)\(-3×\left(\displaystyle\frac{1}{3}a\right)×\left(-\displaystyle\frac{2}{3}a\right)\)\(+a×\left(-\displaystyle\frac{2}{3}a\right)^2\)\(-2a×\left(\displaystyle\frac{1}{3}a\right)\)\(+a×\left(-\displaystyle\frac{2}{3}a\right)\)\(+2\)
\(=\displaystyle\frac{4}{27}a^3-\displaystyle\frac{2}{3}a^2+2\)
\(f(α)+f(β)=2\)であるため、以下の式を作ることができます。
\(\displaystyle\frac{4}{27}a^3-\displaystyle\frac{2}{3}a^2+2=2\)
\(2a^3-9a^2=0\)
\(a^2(2a-9)=0\)
そのため\(a=0,\displaystyle\frac{9}{2}\)のとき、\(f(α)+f(β)=2\)となります。
ただ前述の通り、三次関数が極値をもつためには\(a<0,3<a\)でなければいけません。そのため\(a=0\)は条件を満たすことができず、答えではありません。つまり、答えは\(a=\displaystyle\frac{9}{2}\)になります。
極大値と極小値を利用して足し算または引き算をする場合、解と係数の関係が役に立ちます。極大値と極小値の値がわからなくても、解と係数の関係を利用すれば答えを出すことができるのです。
不等式の証明を微分を用いて行う
また三次関数の不等式を証明する場合、微分を利用することで証明することもあります。微分を利用することによって、常に値が正の数になることを証明するのです。
例えば、以下の三次不等式の証明をしましょう。
- \(0≦x\)のとき、\(x^3+9x≧6x^2\)となる
不等式の証明では、大小の差を比較します。引き算を利用するとき、最小値が常に正(または0)であるとわかると、不等式を証明できます。そこで、不等式を以下のように変えましょう。
\(x^3+9x≧6x^2\)
\(x^3-6x^2+9x≧0\)
\(f(x)=x^3-6x^2+9x\)と考えて微分すると以下のようになります。
\(f'(x)=3x^2-12x+9\)
\(f'(x)=3(x^2-4x+3)\)
\(f'(x)=3(x-1)(x-3)\)
こうして、\(x=1,3\)のときに極値となります。また、\(x=1\)と\(x=3\)のときの値は以下のようになります。
\(f(1)=1-6+9=4\)
\(f(3)=27-54+27=0\)
そのため\(0≦x\)のとき、以下のようになります。
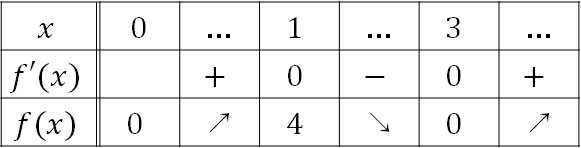
\(0≦x\)のとき、\(f(x)≧0\)となります。そのため、\(x^3+9x≧6x^2\)を証明することができました。
三次関数の極大値と極小値を微分によって求める
三次関数のグラフを描くとき、必ず微分するようにしましょう。極大値と極小値の座標を得るためには、微分することによって傾きがゼロになる部分を見つける必要があります。極大値と極小値がわかれば、グラフを描けるようになります。
ただすべての三次関数で極値があるわけではありません。場合によっては、極大値や極小値をもたないケースもあります。極値があるかどうかを調べるためには、判別式を利用しましょう。
また三次関数のグラフについて、対称性が問われたり、極大値と極小値の和(または差)を問われたりすることがあります。また、三次不等式の証明をしなければいけないこともあります。これらの発展問題についても解けるようにしましょう。
微分することで傾きを知ることができれば、三次関数のグラフの形がわかります。これによって、あらゆる関数のグラフを描けるようになります。