高校数学で学ぶ分野に微分と積分があります。難しい分野の一つでもあり、大学物理を学ぶ人で最も利用する分野でもあります。
そもそも、微分や積分とは何なのでしょうか。微分と積分の概念は難しくなく、中学数学を理解している場合、微分や積分が何なのか理解できます。またなぜ微分や積分が重要であり、どのようなときに利用されるのかわかります。
多くの人で「微分や積分を学ぶのは意味がない」と思うのは、利用する場面を理解できないからです。ただ世の中の現象は微分と積分で説明できることが多いです。
微分と積分を学ぶ前に、なぜこれらの分野が重要なのか理解しなければいけません。そこで微分と積分が何なのかについて、中学数学のみを利用して解説していきます。
もくじ
微分と積分で重要な関数の概念
万有引力の法則を発見した人物としてアイザック・ニュートンが知られています。また彼は物理学者でもあり、数学者でもあります。ニュートンが物理学者と数学者の両方の側面をもつことからも、物理は数学と密接に関係していることがわかります。
数学では、「ニュートンの最も大きな功績が微分・積分の発見」といわれています。
それでは微分・積分を理解する前に、まずは関数を学びましょう。関数とは、一つの数字を入れることによって、答えが出てくる式を指します。
関数は\(y=f(x)\)と記されます。記号を見ると、難しく感じるかもしれません。ただ概念は簡単であり、\(y=f(x)\)は何らかの式を表します。例えば\(y=2x\)の場合、\(2x\)が\(f(x)\)に該当します。また\(x\)に2を代入すると、答えとして4が出てきます。また\(x\)に3を代入すると、答えとして6が出てきます。
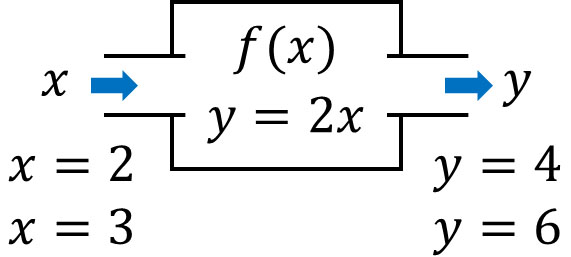
関数によって式はそれぞれ異なり、一次関数かもしれないですし、二次関数かもしれません。つまり\(y=f(x)\)というのは、\(y=2x\)かもしれないし、\(y=x^2+4x-2\)かもしれません。いずれにしても、数字を入力することで答えが出てくるのが関数です。
また\(f(3)\)というのは、\(x=3\)のときの答えを表しています。例えば関数が\(y=2x\)の場合、\(f(3)=2×3=6\)となります。これが関数の概念です。
時間経過と共に変化する軌道や速さを計算する
それでは、どのようなときに微分や積分が利用されるのでしょうか。微分・積分が特に利用されるのは、時間経過と共に変化する場合です。
昔は戦争をするとき、大砲が頻繁に利用されていました。ただ、大砲の軌道は放物線を描きます。これはつまり、時間によって進行方向が変わることを意味します。

また車を発進させるとき、止まっている状態から徐々に速度が速くなっていきます。この場合、時間によって速度が異なります。それでは、変化する速度をどのように計算すればいいのでしょうか。
微分・積分を学ぶ前では、私たちは常に同じ状態の場面を考えます。例えば車が同じ速度で走っていると仮定するとき、一次関数を利用することによって時間・距離・速度を計算することができます。速度が同じ場合、進む距離や到着時間がわかるのです。
ただ実際には、速度は変化します。時間経過と共に軌道や速度が変化する場合、変化を知るための数学が必要です。そこでニュートンによって微分・積分が発見されました。つまり微分・積分というのは、変化するものを調べるための学問なのです。
放物線の傾き(接線)が速さになる
それでは変化する物体について、どのようにしてある一点の様子を知ることができるのでしょうか。時間経過と共に変化するわかりやすい例として二次関数があります。二次関数では、以下のように曲線となります。
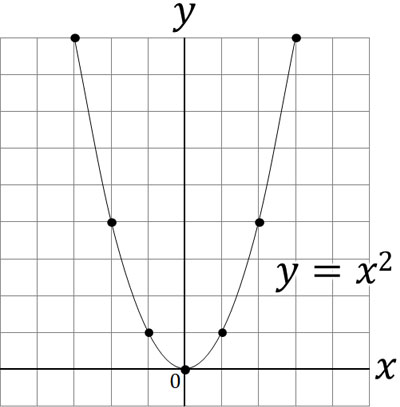
二次関数では、大砲の軌道や車の速度と同じように放物線のグラフになります。車を発進させる場合では、時間経過と共に車のスピードが上昇することで二次関数となります。
例えば\(x\)軸を時間(秒)、\(y\)軸を進んだ距離(m)とすると、\(y\)の変化量(進んだ距離)に対して\(x\)の変化量(経過した時間)を割ることによって速度を計算できます。
例えば、\(y=x^2\)のグラフでは、車が発信して1~3秒のときの平均速度はいくらでしょうか。グラフを確認すると、座標は\((1,1)\)と\((3,9)\)です。つまり、2秒経過することで8m進んでいます。そのため、1~3秒の間の平均速度は毎秒4mです。
- \(\displaystyle\frac{8}{2}=4\)
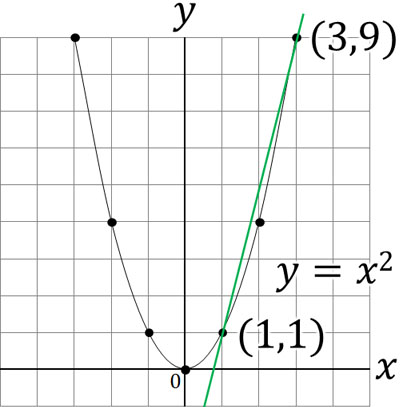
つまり\(x\)軸が時間、\(y\)軸が距離を表すとき、2点を結ぶ線は平均速度を表しています。要は、傾きは速度であると理解しましょう。
一瞬に動く傾きを測定し、グラフの傾きを計算する
ただ二次関数のグラフ(放物線のグラフ)では、時間経過と共に速度が変わります。また私たちが知りたいのは、2点を結ぶ直線の傾き(速さ)ではなく、ある特定のポイントでの速さを知りたいです。そのためには、どのようにすればいいでしょうか。
先ほど、\((1,1)\)と\((3,9)\)の2点を利用して平均速度を求めました。そこで一つの点を基準にして、少しだけ時間が経過した場面を考えましょう。
例えば\(y=x^2\)の関数があるとします。h秒が経過すると、\((x,x^2)\)の座標から\((x+h,(x+h)^2)\)に移動します。このとき、\(x\)軸の変化は以下になります。
\((x+h)-x=h\)
また、\(y\)軸の変化は以下になります。
\(f(x+h)-f(x)\)
\(=(x+h)^2-x^2\)
\(=x^2+2hx+h^2-x^2\)
\(=2hx+h^2\)

そのため、h秒経過するときの平均速度は以下の式によって表されます。
- \(\displaystyle\frac{2hx+h^2}{h}=2x+h\)
ここで、hの値を限りなく0に近づけてみましょう。hを0.000000001秒にするのです。そうすると、2点間の平均速度ではあるものの、hの値が非常に小さいため、実質的に一点での速度を表していることになります。
またhの値は非常に小さく、ほぼ0であるため\(h≒0\)と考えることができます。なお、hを限りなく小さくして0に近づけることを\(\displaystyle \lim_{ h \to 0 }\)と表現します。そのため、以下のように計算します。
- \(\displaystyle \lim_{ h \to 0 } 2x+h=2x\)
こうして\(y=x^2\)の関数では、特定の座標の傾きが\(2x\)になるとわかります。\(y=x^2\)の関数について、\(x=3\)のときの傾き(速さ)は\(2×3=6\)です。また\(x=4\)のときの傾き(速さ)は\(2×4=8\)です。傾きを計算できる新たな関数を導き出すことによって、速さを求めることができるのです。
このように、傾きを計算できる新たな関数を導き出すのが微分です。微分とは、傾きを計算するための数学なのです。
箱の容量が最大になる体積を微分によって計算する
なお実際に微分をするとき、先ほどのような面倒な計算はしません。つまり、h秒が経過したときの傾きを計算、\(\displaystyle \lim_{ h \to 0 }\)を利用して傾きを出すことはしません。そうではなく、公式を利用します。
例えば\(f(x)=ax^n\)を微分するとき、以下のようになります。
- \(f'(x)=a×nx^{n-1}\)
※\(f'(x)\)とは、\(f(x)\)を微分することを意味します。
例えば\(x^3\)であれば、微分すると以下のようになります。
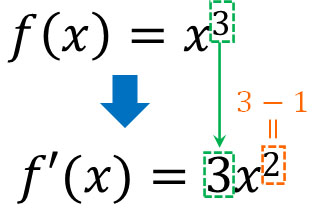
同じように、公式を利用して\(y=f(x)=x^2\)を微分すると、\(y’=2x\)になります。先ほど例として\(y=x^2\)を微分しましたが、公式を利用することによって簡単に\(y’=2x\)を得ることができるのです。
またどのような関数であっても、微分することによって特定のポイントの傾きを出すことができます。そのため、非常に多くの分野で微分が利用されているのです。
それでは、実際に微分を利用してみましょう。以下の問題の答えは何でしょうか。
- 一辺が30cmの紙があります。紙の四隅を\(x\)cm切り取るとき、完成される体積は\(y\)cm3になります。体積が最大になるように切り取るには、紙を何センチ切り取ればいいでしょうか? また、\(y\)の最大値はいくらですか?
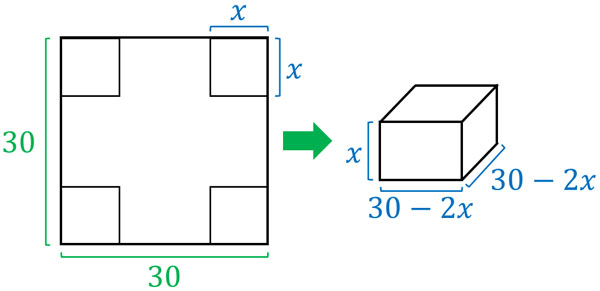
体積の計算式は以下になります。
\(x(30-2x)(30-2x)\)\(=4x^3-120x^2+900x\)
この関数について、\(y\)が最大になる\(x\)の値は何でしょうか。一辺の長さは30cmであるため、\(0<x<15\)です。そこでグラフを描くと、以下のようになります。
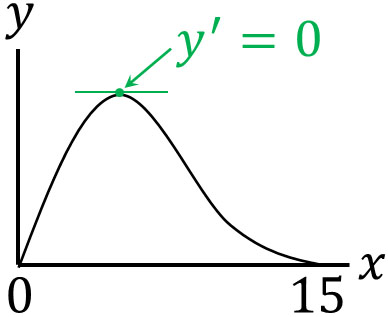
このようにグラフを描くと、傾きが0のときに\(y\)が最大になるとわかります。\(x\)の値が増えると、\(y\)の値が増えます。ただ、ある時点から\(x\)の値が増加するにしたがって、\(y\)の値が減少していきます。そのため、グラフの傾きを調べることによって\(y\)の最大値がわかります。
この問題を解くため、\(f(x)=4x^3-120x^2+900x\)を微分しましょう。以下のようになります。
\(f(x)’=4×3x^2-120×2x+900\)
\(f(x)’=12x^2-240x+900\)
こうして、微分することで新たな関数を得ることができます。次に、\(f'(x)=0\)になる\(x\)の値を見つけましょう。そこで因数分解をします。以下のようになります。
\(f'(x)=12x^2-240x+900\)
\(f'(x)=12(x^2-20x+75)\)
\(f'(x)=12(x-5)(x-15))\)
こうして\(x=5\)または\(x=15\)のとき、傾きが0になるとわかります。ただ\(0<x<15\)なので、\(x=5\)のみが答えです。
\(f(x)=4x^3-120x^2+900x\)の式では、\(x=5\)で傾きが0になります。つまり\(x=5\)のとき、\(y\)が最大になります。そこで\(x\)に5を代入しましょう。
\(f(5)=4×5^3-120×5^2+900×5\)\(=2000\)
こうして、体積の最大は2000cm3になるとわかります。
微分を学ぶとき、なぜ微分が必要になるのか理解できない人がほとんどです。ただ、あなたは微分を利用することによって体積の最大値を求めることができました。そのため、なぜ微分が多くの場面で利用されるのか少しは理解できたと思います。
面積を計算するのが積分
微分を学んだ後、必ず習うことになるのが積分です。微分を理解するというのは、積分を理解するのと意味が同じです。
積分は面積を計算することを意味します。そこで、関数の面積の計算をしてみましょう。例えば\(y=2x\)のグラフでは、直線の下の面積はいくらでしょうか。この関数では、横の長さが\(x\)、たての長さが\(2x\)になります。そのため、面積は以下のように計算できます。
- \(x×2x×\displaystyle\frac{1}{2}=x^2\)
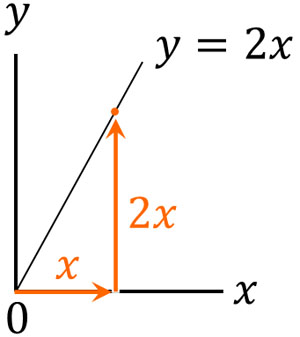
一次関数の面積を出すとき、特に難しいことを考えることなく計算することができます。
曲線の関数で面積はどのように計算するのか
一方で曲線の場合はどのように面積を計算すればいいのでしょうか。例えば、\(y=3x^2\)の面積はどのように計算するのでしょうか。
積分が発見される以前、曲線の面積をどのように計算していたかというと、以下のように曲線の下に多くの長方形を敷きつけることによって計算していました。
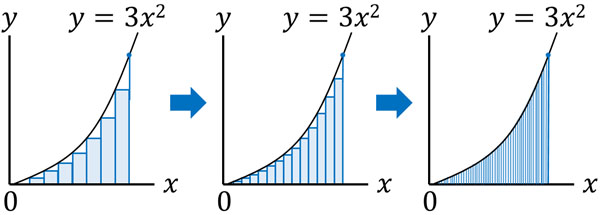
長方形であれば、横とたての長さをかけることによって面積を計算できます。ただ横幅の大きい長方形では、曲線の面積を正確に計算することはできません。一方で横幅が非常に短い長方形を作り、たくさん敷き詰めれば、曲線の下の面積がいくらなのか計算することができます。
正確な値を出すことはできないものの、近似値を計算できるというわけです。
この方法によって計算すると、\(y=3x^2\)の二次関数では、\(x=1\)のときの面積が1になると計算できます。また同じ方法で面積を計算すると、\(x\)が2のときに面積は8になります。\(x\)が3のとき、面積は27になります。
こうして小さい長方形を敷き詰め、面積を計算していくと、面積を計算できる新たな関数として\(y=x^3\)を得ることができます。いずれにしても長方形を利用することによって、面積を計算できることを理解しましょう。
微分と積分は逆の関係にある
面積の計算について、ここまでの話をまとめると以下のようになります。
- \(y=2x\)の面積:\(x^2\)
- \(y=3x^2\)の面積:\(x^3\)
これらの式を見て、何か気づくことはないでしょうか。\(y=x^2\)を微分すると、\(y=2x\)になります。一方、\(y=2x\)を積分すると\(y=x^2\)になります。
また\(x^3\)を微分すると、\(y=3x^2\)になります。一方、\(y=3x^2\)を積分すると\(y=x^3\)になります。
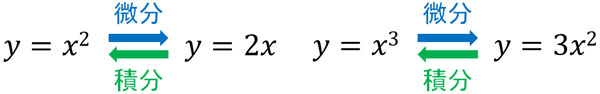
このように、微分と積分は逆の関係になっています。すべての関数について、この関係が成り立つと理解しましょう。
微分の逆が積分であるため、微分の公式を利用することによって積分の公式を作ることができます。例えば\(f(x)=x^n\)を積分する場合、以下のようになります。
- \(\displaystyle\frac{1}{n+1}x^{n+1}+C\)
Cは定数であり、重要ではないので無視をしてもらって問題ありません。微分すると定数Cは消えるため、積分の公式ではCを加えるようになっています。いずれにしても、微分の逆をすることによって積分の公式を作ることができます。
微分と積分で理解する円と球の公式
ここまでの内容を理解すれば、円の公式と球の公式の謎が解けるようになります。私たちは以下の円の公式を習いました。
- 円周の長さ:直径\(×π=2πr\)
- 円周の面積:半径\(×\)半径\(×π=πr^2\)
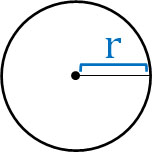
円周の長さを出す公式(\(2πr\))について、rを基準に積分してみましょう。そうすると、円の面積を出す公式(\(πr^2\))になります。また円の面積を出す公式を微分すると、円周の長さを求める公式になります。
先に解説した通り、曲線の下の面積を計算するとき、横幅が非常に短い長方形を寄せ集めることによって、面積の計算をしました。同じように考えると、円の面積というのは、わずかな厚さをもつ円周を非常にたくさん寄せ集めることによって計算できます。
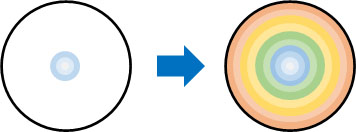
円周の長さと円の面積を計算するとき、微分と積分を理解していれば、互いの関係性を理解できるようになります。
次に球の公式を確認しましょう。球の表面積と球の体積を出す公式は以下になります。
- 球の表面積:\(4πr^2\)
- 球の体積:\(\displaystyle\frac{4}{3}πr^3\)
球の表面積を出す公式について、rに着目して積分しましょう。そうすると、球の体積を出す公式になります。また球の体積を出す公式を微分すると、球の表面積を出す公式になります。
わずかな厚さをもつ球について、表面積(球の殻)を何枚も重ねるとどうなるでしょうか。薄い表面が重なることによって、最終的に球の体積になります。そのため球の表面積を積分すると、球の体積を得ることができるのです。
ロケットの位置は微分・積分で計算できる
それでは、微分と積分が有効であることをさらに理解しましょう。大学物理では微分と積分が頻繁に利用されます。力学や熱、電磁気、原子とすべての物理で微分・積分が活躍します。物理というのは、数学でもあるのです。
先ほど解説した通り、距離を微分すると速さになります。また速さを積分すると、距離になります。
それでは、速さを微分するとどうなるのでしょうか。速さを微分する場合、加速度を求めることができます。また加速度を積分すると、速さを出せます。
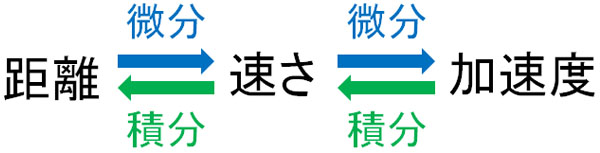
高校物理を習っていない場合、加速度が何かわからないかもしれません。加速度というのは、どれだけ加速するのかを意味します。加速度が正の値の場合、時間経過と共にスピードは速くなります。
それでは、ロケットを打ち上げるとします。空中にある物体は放物線を描くことからわかる通り、二次関数のグラフとなります。仮にロケットを打ち上げるとき、経過時間\(x\)秒と進む距離(高度)\(y\)mの関係が\(y=10x^2\)の場合、\(x\)秒後の速度や加速度はいくらでしょうか。
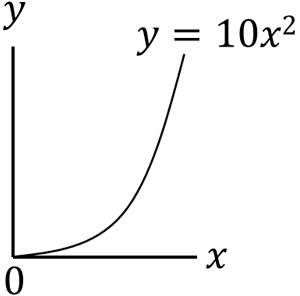
距離(高度)を求めることができる関数を微分すれば、速さを計算できる新たな関数を得ることができます。そこで、\(y=10x^2\)を微分すると以下のようになります。
- \(y’=20x\)
そのため、例えば10秒後の速度は毎秒200mです。また、20秒後の速度は毎秒400mです。こうして、速度を計算することができます。
次に加速度を計算しましょう。速さを微分すると加速度になります。\(y’=20x\)を微分すると以下のようになります。
- \(y”=20\)
こうして、加速度は20m/s2であり一定です。同じ加速度にて、スピード上昇していくというわけです。
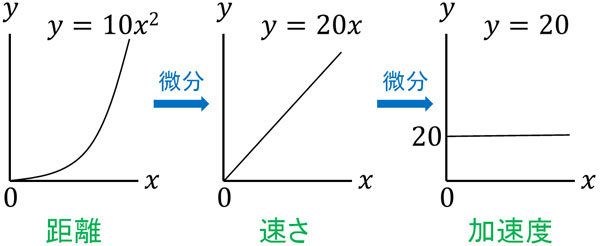
このように微分を利用することによって、将来の速度や加速度を計算できるようになります。
高校物理で微分・積分を利用することはほぼないかもしれません。ただ物理の公式というのは、微分・積分を利用することによって導くことができます。また物理現象を微分と積分で説明できるという事実は、私たちの身の回りは微分と積分で成り立っていることが多いことを意味しています。
もちろん力学や電磁気、熱、原子などの物理分野だけでなく、統計学や金融、経済についても微分と積分で説明できるケースが多いです。あらゆる分野で利用されるため、微分と積分を私たちは高校数学で学ぶのです。
微分と積分の概要を理解する
微分・積分とは何かについて、できるだけわかりやすく解説してきました。ここまでの内容であれば、中学数学を理解している人であれば全員が微分・積分が何を意味しているのか分かると思います。
数学を学ぶとき、問題を解くことばかり考えがちです。そのため、なぜ微分や積分が重要なのか理解できない人が多いです。ただ、私たちの周辺には微分と積分で説明できる現象が多いです。「車や飛行機が発進する」「空中を飛んでいる鳥」など、これらは微分と積分で現象を説明できます。
また微分と積分の概要を学ぶとき、ここまで解説したように簡単な数学によって理解できます。微分は傾きを計算するための方法であり、積分は面積を計算するための方法です。また、微分と積分は逆の関係にあります。
これらを理解すれば、微分と積分の基本がわかります。微分と積分には公式があるため、公式を利用することによってグラフの傾きまたは面積を計算できるようになります。






