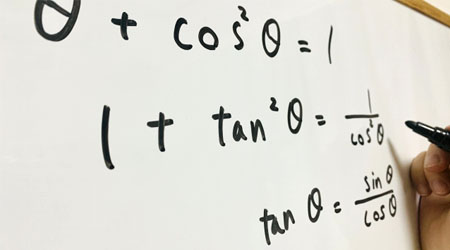三角比を利用することによって図形の面積を計算することができます。sinθを利用することによって、三角形のたての長さを出すことができます。その後、面積を計算するのです。なお三角比の値を出すためには、正弦定理や余弦定理を利用することもあります。
三角形の面積を計算することができれば、四角形や五角形など、多角形の面積を計算できるようになります。多角形の面積では、三角形を利用して計算できます。なお三角比と図形の面積では、ヘロンの公式を学びます。ただ、重要ではない公式なので覚えなくてもいいです。
また三角比と図形の問題では、円が関わる問題を出されることがあります。三角形が関わる円には外接円と内接円があり、どのように半径を出せばいいのか理解しましょう。
三角比では図形と一緒に問題を出されます。そこで、どのように辺の長さや面積を計算すればいいのか解説していきます。
もくじ
sinθで三角形のたての長さと面積を計算する
三角比を利用することによって、三角形の面積を計算することができます。公式としては以下になります。
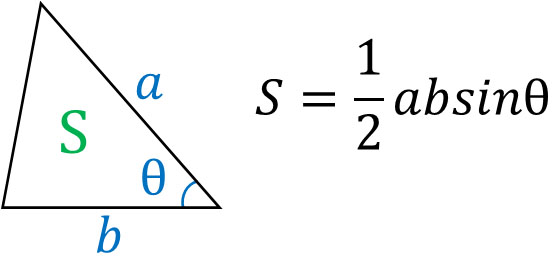
2辺とその間にある角度がわかっている場合、sinθを利用することによって三角形の面積を計算することができます。それでは、なぜこの公式が成り立つのでしょうか。
この公式については、覚えてもいいし覚えなくてもいいです。たとえ公式を覚えなかったとしても、三角形の面積を計算することができるからです。
\(a×sinθ\)によって、三角形のたての長さを出すことができます。また、三角形の面積を出す公式は以下になります。
- 面積 = 横 × たて ÷ 2
そのため、横の長さ(\(b\))とたての長さ(\(a×sinθ\))をかけた後、2でわることによって三角形の面積を計算できます。
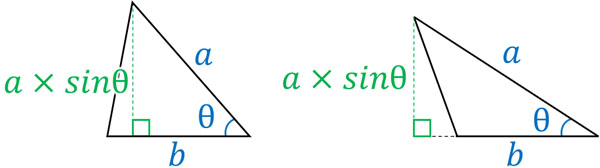
3つの角がすべて鋭角の三角形であっても、鈍角をもつ三角形であっても、三角形の面積は\(S=\displaystyle\frac{1}{2}absinθ\)を利用することによって計算できます。
・三角形の面積を計算する
それでは、実際に三角形の面積を計算してみましょう。以下の三角形の面積はいくらでしょうか。
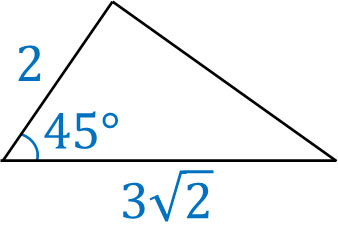
この三角形のたての長さは\(2×sin45°=\displaystyle\frac{2}{\sqrt{2}}\)です。また、横の長さは\(3\sqrt{2}\)です。そのため、面積は以下のようになります。
- \(\displaystyle\frac{2}{\sqrt{2}}×3\sqrt{2}×\displaystyle\frac{1}{2}=3\)
こうして、三角形の面積を計算できます。
多角形の面積の計算方法
次に四角形や五角形など、多角形の面積を計算できるようにしましょう。多角形の面積を計算するとき、方法としては「三角形を利用して面積を計算する」ことがあります。
例えばABとDCが平行となる以下の台形について、面積はいくらでしょうか。
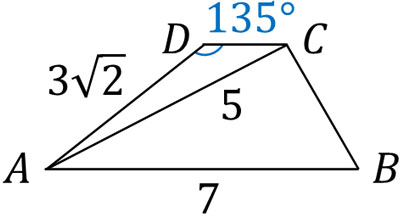
まず、DCの長さを計算しましょう。余弦定理より、以下のようになります。
\(5^2=(3\sqrt{2})^2+DC^2-2×3\sqrt{2}×DC×cos135°\)
\(25=18+DC^2+6DC\)
\(DC^2+6DC-7=0\)
\((DC-1)(DC+7)=0\)
辺の長さであるため、\(DC>0\)です。そのため、DC=1です。次に、台形の縦の長さを計算しましょう。以下のように図を作れば、\(3\sqrt{2}×sinA\)\(=3\sqrt{2}×sin45°\)によってたての長さがわかります。
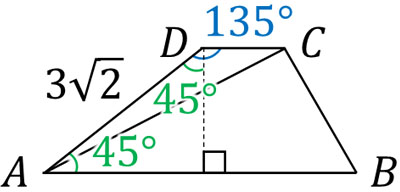
\(3\sqrt{2}×sin45°=3\)です。そのため、台形の面積を出す公式を利用することによって、以下のように計算できます。
\((1+7)×3×\displaystyle\frac{1}{2}=12\)
こうして、三角形を利用することによって台形の面積を計算できます。四角形や五角形、六角形など、多角形の面積は正弦定理と余弦定理を利用して計算するようにしましょう。
ヘロンの公式で面積を計算する
なお三角比を利用して図形の面積を出すとき、ヘロンの公式を習います。\(2s=a+b+c\)とするとき、三角形の面積(S)は以下の公式を利用することによって計算できます。
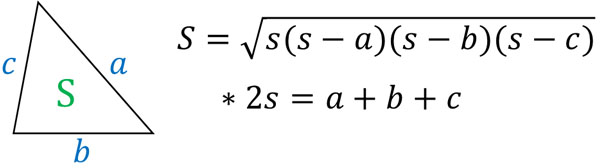
ヘロンの公式を利用すれば、角度がわからなかったとしても、3つの辺を利用することによって面積を出すことができます。
余弦定理を使い、ヘロンの公式を無視する
ただヘロンの公式は複雑です。また利用する場面は少なく、この公式を覚える意味はありません。もちろんヘロンの公式を覚えてもいいですが、ほぼ役に立ちません。そこで3辺の長さが与えられている面積の問題では余弦定理を利用しましょう。
余弦定理であれば、3辺を利用することによってcosθの値を得ることができます。またcosθがわかれば、sinθの値もわかります。そのため、三角形の面積を計算できます。
例えば、以下の三角形の面積はいくらでしょうか。
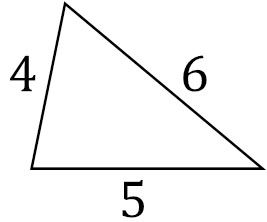
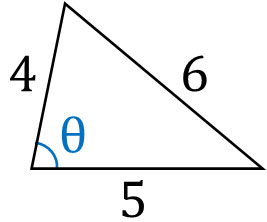
ヘロンの公式を利用すれば、簡単に面積を計算できます。ただ前述の通りヘロンの公式を覚える必要はないため、余弦定理を利用して計算しましょう。以下のようになります。
\(6^2=5^2+4^2-2×4×5×cosθ\)
\(36=25+16-40cosθ\)
\(40cosθ=5\)
\(cosθ=\displaystyle\frac{1}{8}\)
こうして、cosθの値を出すことができました。
次にsinθの値を出します。\(sin^2θ+cos^2θ=1\)であるため、以下のように計算できます。
\(sin^2θ+\displaystyle\frac{1}{64}=1\)
\(sin^2θ=\displaystyle\frac{63}{64}\)
\(0°<θ<180°\)であるため、\(sinθ>0\)。
\(sinθ=\displaystyle\frac{3\sqrt{7}}{8}\)
次に、三角形の面積を計算しましょう。\(sinθ=\displaystyle\frac{3\sqrt{7}}{8}\)、横の長さは5であるため、これまで説明した知識を利用すると以下の式を作ることができます。
\(\displaystyle\frac{1}{2}×5×4×sinθ\)
\(10×\displaystyle\frac{3\sqrt{7}}{8}\)
\(=\displaystyle\frac{15\sqrt{7}}{4}\)
こうして、ヘロンの公式を利用しなくても三角形の面積を計算できます。
三角形の内接円の面積と半径
なお図形の問題を解くとき、三角形に内接する円が出題されるケースがあります。以下のように、三角形の内側に接する円を内接円といいます。
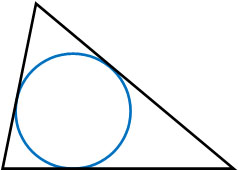
内接円の問題では、三角形の面積を計算したり、内接円の半径を計算したりします。内接円の面積\(S\)を計算するとき、公式があります。内接円の半径を\(r\)とすると、以下の公式が成り立ちます。
- \(S=\displaystyle\frac{1}{2}r(a+b+c)\)
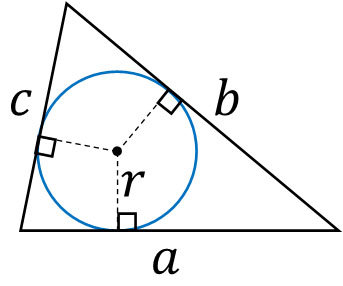
ただ、この公式は覚えないようにしましょう。理由としては、簡単に公式を作ることができるからです。以下のように三角形を分割して、3つの面積を計算してみましょう。
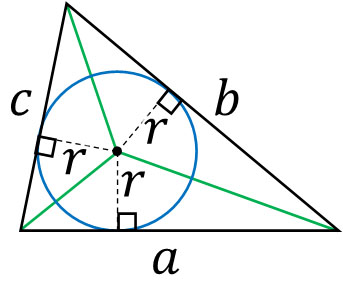
円の中心から三角形の各辺までの距離は等しいです。また接線に対して円の中心から線を引くと、直角になります。そこで、それぞれの三角形について面積を計算しましょう。そうすると、先ほどの公式を作ることができます。
\(\displaystyle\frac{1}{2}ar+\displaystyle\frac{1}{2}br+\displaystyle\frac{1}{2}cr\)
\(=\displaystyle\frac{1}{2}r(a+b+c)\)
公式の作り方を理解していれば、先ほどの公式を覚える必要はありません。
内接円は三角形の面積、外接円は正弦定理で半径を求める
なお三角形は必ず内接円と外接円をもちます。内接円の半径を計算するとき、必ず三角形の面積を利用しましょう。先ほど解説した公式には、内接円の半径が含まれています。そのため、内接円の半径を計算できるのです。
一方で外接円の半径を計算する場合、正弦定理を利用しましょう。正弦定理には、公式の中に外接円の半径が含まれています。
例えば以下の三角形について、内接円の半径と外接円の半径はいくらでしょうか。
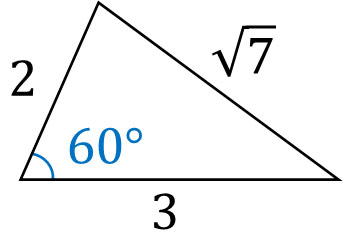
内接円の半径を出すため、三角形の面積を計算しましょう。以下のようになります。
\(\displaystyle\frac{1}{2}×3×2×sin60°\)
\(=3×\displaystyle\frac{\sqrt{3}}{2}\)
\(=\displaystyle\frac{3\sqrt{3}}{2}\)
次に、内接円の半径を計算しましょう。内接円の半径を\(r\)とすると、以下のように式を作れます。
\(\displaystyle\frac{3\sqrt{3}}{2}=\displaystyle\frac{1}{2}×2r+\displaystyle\frac{1}{2}×3r+\displaystyle\frac{1}{2}×\sqrt{7}r\)
\(3\sqrt{3}=2r+3r+\sqrt{7}r\)
\(3\sqrt{3}=r(5+\sqrt{7})\)
\(r=\displaystyle\frac{3\sqrt{3}}{5+\sqrt{7}}\)
有理化すると
\(r=\displaystyle\frac{3\sqrt{3}(5-\sqrt{7})}{(5+\sqrt{7})(5-\sqrt{7})}\)
\(r=\displaystyle\frac{15\sqrt{3}-3\sqrt{21}}{18}\)
\(r=\displaystyle\frac{5\sqrt{3}-\sqrt{21}}{6}\)
次に外接円の半径を計算してみましょう。先ほど述べた通り、外接円の半径を計算するときは正弦定理を利用します。以下の式を作りましょう。
\(\displaystyle\frac{\sqrt{7}}{sin60°}=2R\)
\(\sqrt{7}÷\displaystyle\frac{\sqrt{3}}{2}=2R\)
\(\sqrt{7}×\displaystyle\frac{2}{\sqrt{3}}=2R\)
\(\displaystyle\frac{\sqrt{7}}{\sqrt{3}}=R\)
有理化すると
\(R=\displaystyle\frac{\sqrt{21}}{3}\)
こうして、外接円の半径を計算できます。計算をするとき、内接円の半径と外接円の半径では利用する公式が異なることを理解しましょう。
三角比を利用し、図形の面積と円の半径を求める
多くの場面で三角比が利用されます。sinθやcosθを利用することによって、三角形の辺の長さだけでなく、図形の面積を求めることができるのです。
解説した公式としては、三角形の面積を出す公式やヘロンの公式、内接円の半径を出す公式があります。ただ、これらの公式を覚える必要はありません。これらの公式は作ることができます。そのため、絶対に覚えなければいけない公式ではありません。
そこで問題が出されたとき、辺の長さや角度を利用して面積(または円の半径)を計算しましょう。また辺の長さや角度がわからない場合、正弦定理や余弦定理を利用するといいです。
三角比を利用すれば、三角形のたての長さを得ることができます。そのため三角形の面積を計算できます。そこから発展させれば、ヘロンの公式なしに面積を計算したり、内接円の半径を導くことができたりします。どのようにして公式を作ればいいのか理解しましょう。