直線の方程式を得ることは重要です。傾きと切片がわかれば、直線の方程式を作ることができます。そこで、ほかの方法によっても直線の方程式を得られるようになりましょう。
点を通る直線であれば、傾きがわかれば直線の方程式を得られます。また2点を通る直線についても、直線の方程式を作ることができます。それに加えて、平行条件と垂直条件を利用して直線の方程式を計算しましょう。
これらの内容を利用することにより、2直線の交点を通る直線を計算できたり、定点を通る直線を得ることができたりします。
それでは、どのように考えて直線の方程式を計算すればいいのでしょうか。直線の方程式の作り方や2直線の関係を解説していきます。
もくじ
直線の方程式と点を通る直線
直線の方程式は既に学んでいます。傾き\(a\)、切片\(b\)の直線は\(y=ax+b\)によって表すことができます。
それでは傾き\(a\)の直線について、点A\((x_1,y_1)\)を通る直線はどのように表せばいいでしょうか。切片を計算することによって直線を得ることは可能です。ただ計算が面倒であり、計算なしに直線の式を作れるようになりましょう。傾きと座標を利用すると、直線の方程式は以下のようになります。
- \(y-y_1=a(x-x_1)\)
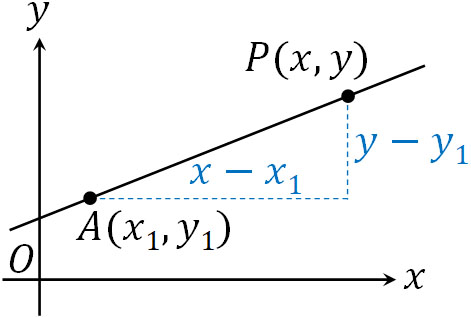
傾きは必ず\(a\)になります。また、直線の傾きを\(\displaystyle\frac{y-y_1}{x-x_1}\)と表すことができます。\(\displaystyle\frac{y-y_1}{x-x_1}=a\)であるため、\(y-y_1=a(x-x_1)\)となります。
異なる2点を通る直線の求め方
次に、異なる2点を通る直線を計算しましょう。\(y=ax+b\)に座標を代入して連立方程式を解き、傾きと切片を計算することによって直線の式を得ることができます。それでは、より簡単な方法によって直線の方程式を得ることはできないのでしょうか。
先ほど、傾きを利用して公式\(y-y_1=a(x-x_1)\)を得ることができました。同様に、傾きが同じであることを利用して、異なる2点を通る直線の式を作りましょう。
例えば、点A\((x_1,y_1)\)と点B\((x_2,y_2)\)を通る直線はどのように表すことができるでしょうか。直線の傾きは共通しています。点Aに対する傾きは\(\displaystyle\frac{y-y_1}{x-x_1}\)です。また点Aと点Bによる傾きは\(\displaystyle\frac{y_2-y_1}{x_2-x_1}\)です。そのため、以下の式を作ることができます。
- \(\displaystyle\frac{y-y_1}{x-x_1}=\displaystyle\frac{y_2-y_1}{x_2-x_1}\)
- \(y-y_1=\displaystyle\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)
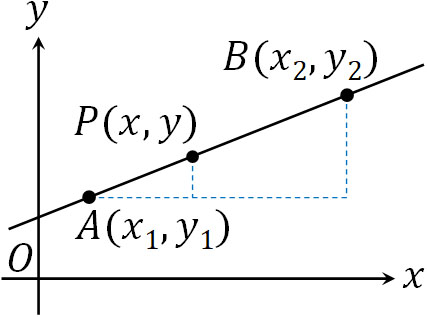
どちらの式を利用しても方程式を得ることができます。なお公式を覚えるのではなく、なぜこれらの公式が有効なのかを学びましょう。そうすれば、いつでも公式を作れるようになります。
2直線の平行条件と垂直条件
ここまでの説明より、直線の方程式を得るときに傾きが重要であることがわかります。2つの直線の関係を表すとき、ひんぱんに利用される関係が平行と垂直です。2つの直線が平行な場合、傾きは必ず同じになります。それぞれの直線の傾きが\(a_1\)と\(a_2\)の場合、\(a_1=a_2\)です。
また2つの直線が垂直な場合、傾きをかけると-1になります。つまり、\(a_1a_2=-1\)です。これが垂直条件です。
平行条件と垂直条件は基本的な内容であるため、必ず覚える必要があります。
定点を通る直線の方程式
それでは、2直線が関わる応用問題を解けるようになりましょう。まず、定点を通る直線の方程式を確認していきます。以下の問題の答えは何でしょうか。
- \(k\)を定数とします。直線\((2+k)x+(1-3k)y-5k-3=0\)は\(k\)の値に関係なく定点Aを通ります。定点Aの座標は何ですか。
\(k\)の値に関係なく式が成り立つというのは、\(k\)に関する恒等式と考えることができます。そこで、\(k\)がどのような値であっても成り立つように、\(k\)を利用して整理しましょう。以下のようになります。
\((2+k)x+(1-3k)y-5k-3=0\)
\((y+2x-3)+(-3y+x-5)k=0\)
\(k\)の値に関係なくこの式が成り立つためには、\(y+2x-3=0\)かつ\(-3y+x-5=0\)である必要がありあす。そこで、この式を解きましょう。
\(\begin{eqnarray} \left\{\begin{array}{l}3y+6x-9=0\\-3y+x-5=0\end{array}\right.\end{eqnarray}\)
\(7x=14\)
\(x=2\)
\(x=2\)であるため、\(y=-1\)です。そのため、定点Aの座標は\((2,-1)\)とわかります。
2直線の交点を通る直線
先ほど、2直線の方程式に対して定数\(k\)を加えることにより、特定の点を通る直線を表すことができました。
2つの直線を利用することにより、交点を計算できます。さらに、定数\(k\)を利用することで、「2直線の交点を通る直線」を表現できるのです。この性質を利用して、以下の問題を解きましょう。
- \(x+y-4=0\)と\(2x-y+1=0\)の交点を通り、直線\(x+2y+1=0\)に平行な直線の方程式を求めましょう。
連立方程式を利用して\(x+y-4=0\)と\(2x-y+1=0\)の交点の座標を計算し、直線の方程式を計算することは可能です。連立方程式を利用すると、2直線の交点は\((1,3)\)とわかります。こうして、傾きを利用することで直線の方程式を得られます。
ただ、より難易度の高い応用問題を解く場合、定点を通る直線の方程式を利用して問題を解けるようになることが重要です。そこで、2直線の定点と平行条件を利用して計算してみましょう。
\(x+y-4=0\)と\(2x-y+1=0\)の交点を通る直線の方程式は以下のように表すことができます。
- \((x+y-4)k+(2x-y+1)=0\)
※\((x+y-4)+(2x-y+1)k=0\)でも問題ない。
この式を\(x\)と\(y\)について整理すると以下のようになります。
\((k+2)x+(k-1)y-4k+1=0\)
この式と直線\(x+2y+1=0\)が平行である必要があります。直線\(x+2y+1=0\)の傾きは\(-\displaystyle\frac{1}{2}\)です。また、\((k+2)x+(k-1)y-4k+1=0\)の傾きは\(-\displaystyle\frac{k+2}{k-1}\)です。そのため、以下の式を作れます。
\(-\displaystyle\frac{k+2}{k-1}=-\displaystyle\frac{1}{2}\)
\(2k+4=k-1\)
\(k=-5\)
\(k=-5\)であるため、以下のように計算して直線の方程式を求めましょう。
\(-5(x+y-4)+(2x-y+1)=0\)
\(-3x-6y+21=0\)
\(x+2y-7=0\)
こうして、直線の方程式は\(x+2y-7=0\)と計算できました。
2直線の共有点と解:三角形を作らない条件
なお\(a_1x+b_1y+c_1=0\)と\(a_2x+b_2y+c_2=0\)の2直線の共有点について、以下の関係にあります。
- 2直線が1つの点で交わる:2つの式の連立方程式は1つの解をもつ
- 2直線が平行:2つの式の連立方程式は解がない
- 2直線が一致:2つの式の連立方程式は無数の解をもつ
当たり前ではありますが、これらの関係があります。それでは、以下の問題を解いてみましょう。
- 3直線\(x+y-4=0\)、\(2x-y+1=0\)、\(3x-ay-a=0\)について、三角形を作らない定数\(a\)の値を求めましょう。
3つの直線が三角形を作らない条件は以下のケースです。
- 3直線が1点で交わる
- 2直線が平行
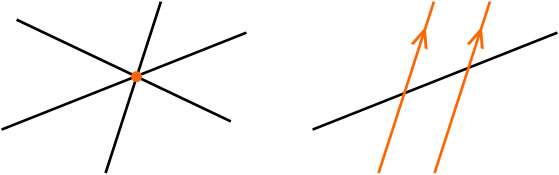
そこで、それぞれのケースで場合分けをしましょう。
・3直線が1点で交わるケース
\(x+y-4=0\)と\(2x-y+1=0\)を利用して連立方程式を解くと、交点は\((1,3)\)とわかります。直線\(3x-ay-a=0\)が\((1,3)\)を通れば、3直線が1点で交わります。そのため、以下のように計算しましょう。
\(3-3a-a=0\)
\(a=\displaystyle\frac{3}{4}\)
こうして、\(a=\displaystyle\frac{3}{4}\)のときに3直線は三角形を作らないとわかりました。
・2直線が平行のケース
\(x+y-4=0\)と\(2x-y+1=0\)は平行ではありません。そのため、\(3x-ay-a=0\)が\(x+y-4=0\)または\(2x-y+1=0\)と平行な場合、3直線は三角形を作りません。2直線が平行というのは、傾きが同じであることを意味しています。そこで、傾きが同じとなる\(a\)を計算しましょう。
\(3x-ay-a=0\)の傾きは\(\displaystyle\frac{3}{a}\)です。\(x+y-4=0\)の傾きは-1なので、以下のように計算しましょう。
\(\displaystyle\frac{3}{a}=-1\)
\(a=-3\)
また\(2x-y+1=0\)の傾きは2なので、計算は以下のようになります。
\(\displaystyle\frac{3}{a}=2\)
\(a=\displaystyle\frac{3}{2}\)
こうして、\(a=\displaystyle\frac{3}{4}\)に加えて\(a=-3\)と\(a=\displaystyle\frac{3}{2}\)も答えであるとわかります。
直線の方程式を利用し、2直線の関係を計算する
図形では、直線の方程式を得る計算問題がひんぱんに出されます。そこで傾きと切片を利用して一次方程式を得る方法だけでなく、その他の公式を利用することによっても直線の方程式を計算できるようになりましょう。
また2直線の関係で平行と垂直は重要です。平行では傾きが同じになり、垂直では2つの傾きをかけると-1になります。平行条件と垂直条件は必ず覚えなければいけません。
これらの関係を利用して、応用問題を解きましょう。連立方程式を解いて座標を得たり、2直線が定点を通る条件式を作ったりするのです。
2直線(または3直線)を利用して計算しなければいけない問題はひんぱんに出題されます。そこで直線の方程式を利用して、計算問題を解けるようになりましょう。