集合と命題の条件：命題の否定と集合の必要条件・十分条件

集合と命題を学ぶとき、命題に対する条件を理解しなければいけません。つまり、提示されている命題が正しいかどうかを判断できるようにするのです。命題が部分集合になっている場合、その命題は正しいです。

また集合と命題では補集合を学びます。提示されている命題（集合）の否定をすると補集合になります。そこで、命題の否定をどのようにすればいいのか学びましょう。

提示されている命題が正しいのか間違っているのかを判断できるようになれば、必要条件と十分条件について理解できるようになります。単語は難しいものの、解き方を理解すれば答えを出すことができます。必要条件と十分条件では「必ず」という単語を利用すると解きやすくなります。

これらの知識は例えばプログラミングで役立ちます。与えられた情報について、コンピューターが正しいのか間違っているのかを判断し、情報を処理するのです。そこで、命題と条件の内容や必要条件と十分条件の解き方を解説していきます。

1 命題と条件とは何かを理解する
- 1.1 集合と命題では、部分集合かどうかを見極める
- 1.2 命題の否定ではド・モルガンの法則を利用する
2 必要条件と十分条件の見分け方
- 2.1 両方を満たす場合は必要十分条件
3 集合と命題での条件や否定、必要条件・十分条件

命題と条件とは何かを理解する

「正しいか正しくないか」について明確に決まる文章や式を命題といいます。例えば、以下は命題です。

円周率と直径を掛けると、円周の長さを得られる

小学校の算数では、円周を出す公式を学びます。円周率と直径を掛けることによって、円周の長さを計算することができます。

また命題が正しい場合、その命題は真です。また命題が間違っている場合、その命題は偽です。そのため、先ほどの命題は真です。一方、以下の命題は偽です。

3は10よりも大きい

数を比較するとき、3は10よりも小さいです。そのため、この命題は偽です。いずれにしても、正しいのか間違っているのか判断できるのが命題です。そのため、以下は命題ではありません。

彼は金持ちだ

金持ちの基準は人によって異なります。正しいのか間違っているのか判断できないので、これは命題ではありません。

・命題と条件の性質

ただ、命題に記されている数字が変わることによって、命題が真になったり偽になったりすることがあります。例えば、以下の文章を考えてみましょう。

\(x\)は1よりも大きい

\(x\)が3の場合、この命題は真です。一方で\(x\)が0の場合、この命題は偽です。このように\(x\)や\(y\)、\(a\)などの変数を含む場合、真なのか偽なのかが変わります。こうした変数を含む式を条件といいます。

集合と命題では、部分集合かどうかを見極める

多くの場合、命題は「pならばq」と記されます。「\(p⇒q\)」と表現されることもあります。なお、命題（Proposition）の頭文字を取ってpを利用します。またアルファベット順では、pの次がqです。そのため集合と命題ではqを利用します。

それでは、どのようにpとqを判断すればいいのでしょうか。例えば、以下の命題があるとします。

\(a≧0\)であれば、\(a\)は-3よりも大きい

この命題では、pは\(a≧0\)です。また、「\(a\)は-3よりも大きい」がqです。この場合、真なのか偽なのか答えるようにしましょう。

なお、真なのか偽なのか確認するときに「必ず」という言葉を利用すると判断しやすくなります。つまり、「\(a≧0\)ならば、必ず\(a\)は-3よりも大きい」と文章を変えます。その後、この文章が正しいかどうかを判断しましょう。そうすると、\(p⇒q\)は真であるとわかります。

この場合、pはqの部分集合です。つまり以下のような集合P（pの集合）と集合Q（qの集合）について、\(P⊂Q\)の関係が成り立ちます。

-3よりも大きい数としては-2や-1を含みます。また、正の数も集合Qの一部です。一方で集合Pの場合、\(a≧0\)なので-2や-1は含みません。そのため、\(P⊂Q\)となります。ベン図を利用すれば「\(p⇒q\)が真のとき、\(P⊂Q\)が成り立つ」とわかります。

それでは、命題が偽の場合はどのようになるのでしょうか。先ほどの命題について、pとqを入れ替えてみましょう。以下のようになります。

\(a\)が-3よりも大きいならば、\(a≧0\)

\(a\)が-3よりも大きければ、必ず\(a≧0\)になるわけではありません。\(a\)が-2や-1の場合、\(a≧0\)を満たしません。そのため、この命題は偽となります。命題を満たさない要素が1つでもある場合、その命題は偽です。

ちなみに、「\(p⇒q\)」と「\(q⇒p\)」の両方を満たす場合はどうなるのでしょうか。例として、以下の命題を考えてみましょう。

\(a=0\)ならば、\(a^2=0\)

\(a=0\)の場合、必ず\(a^2=0\)です。そのため、「\(p⇒q\)」は真です。また\(a^2=0\)の場合、必ず\(a=0\)です。そのため、「\(q⇒p\)」は真です。この場合、集合Pと集合Qは等しい（P＝Q）です。

命題の否定ではド・モルガンの法則を利用する

ここまで、命題について確認してきました。このとき、条件pの反対の集合を作ることができます。pの反対というのは、「pではない」ことを意味します。例えば、以下の条件があるとします。

\(a≧0\)

この条件の反対（否定）は\(a<0\)です。それではより複雑な条件について、否定するにはどのようにすればいいでしょうか。例えば、以下の条件の否定はどのようにすればいいでしょうか。

\(a>0\)かつ\(b>0\)

この否定を述べるためには、ド・モルガンの法則を利用するようにしましょう。以下がド・モルガンの法則です。

\(\overline{A∪B}=\overline{A}∩\overline{B}\)
\(\overline{A∩B}=\overline{A}∪\overline{B}\)

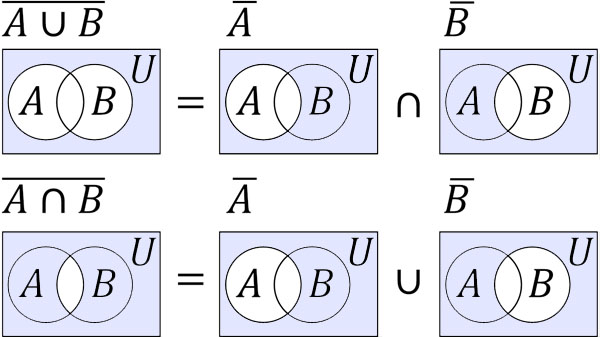
集合と命題では補集合を学びます。集合Pを含まない集合が\(\overline{P}\)です。また集合Qを含まない集合が\(\overline{Q}\)です。条件p（集合P）の反対というのは、\(\overline{P}\)を探すことと意味が同じです。

そのため\(\overline{A∪B}\)や\(\overline{A∩B}\)を\(\overline{P∪Q}\)や\(\overline{P∩Q}\)とみなすことによって、条件の反対を述べることができます。つまり否定を述べるとき、条件pと条件qの反対を述べると同時に、「かつ」と「または」を入れ替えるようにしましょう。

このように考えると、\(a>0\)かつ\(b>0\)の否定は\(a≦0\)または\(b≦0\)です。なお、ド・モルガンの法則は条件が増えたとしても考え方は同じです。例えば、以下の条件の否定はなんでしょうか。

\(a=b=c=0\)

\(a=b=c=0\)は「\(a=0\)かつ\(b=0\)かつ\(c=0\)」です。そのため、\(a=b=c=0\)の否定は「\(a≠0\)または\(b≠0\)または\(c≠0\)」です。

必要条件と十分条件の見分け方

ここまでの内容を学べば、必要条件と十分条件について理解できるようになります。先ほど、「\(p⇒q\)」が成立するかどうかを確認しました。また、「\(q⇒p\)」が成立するかどうかも確認しました。これができれば、必要条件なのか十分条件なのか判断できるようになります。

まず、必要条件や十分条件とは何なのでしょうか。これらの言葉を日常で使うことがないため、難しいように感じてしまいます。ただ考え方は簡単であり、以下のように理解しましょう。

pならばqが成り立つ場合：十分条件
qならばpが成り立つ場合：必要条件

例えば、以下の命題を考えてみましょう。

\(x=2\)ならば、\(x^2=4\)

この命題では、pならばqが成り立ちます。\(x=2\)であれば、答えは必ず\(x^2=4\)です。一方、qならばpは成り立ちません。\(x^2=4\)の答えは\(x=±2\)です。pならばqのみが真のため、この命題は十分条件です。

この場合、「pはqであるための十分条件である」と表現されます。先ほどの命題であれば、「\(x=2\)は\(x^2=4\)であるための十分条件である」という表現になります。またpならばqのみが真となるため、十分条件では\(P⊂Q\)が成り立ちます。この理由は先ほど述べたとおりです。

・必要条件ではpとqを入れ替える

一方で必要条件はどのようになるのでしょうか。以下の命題を考えてみましょう。

\(|x-2|>1\)ならば、\(x>3\)

この命題では、pならばqは偽です。\(|x-2|>1\)の答えは\(x<1,3<x\)です。\(x\)には0や-1も含まれるため、\(|x-2|>1\)ならば、必ず\(x>3\)になることはありません。

一方、qならばpは成り立ちます。先ほどの命題について、pとqを入れ替えましょう。以下のようになります。

\(x>3\)ならば、\(|x-2|>1\)

\(x>3\)ならば、必ず\(|x-2|>1\)です。このようにpとqを入れ替えて成り立つ場合、その命題は必要条件です。この場合、「qはpであるための必要条件である」と表現されます。先ほどの命題であれば、「\(x>3\)は\(|x-2|>1\)であるための必要条件である」という表現になります。

またqならばpが真となるため、\(Q⊂P\)が成り立ちます。集合Qというのは、Pの部分集合となります。部分集合であるため、条件qは必ず成り立ちます。

命題では最初に「\(p⇒q\)」が真かどうかを考えます。真であれば十分条件です。次に「\(q⇒p\)」が真かどうかを考えます。真であれば必要条件です。そのため必要条件なのか十分条件なのかについて、「十分 ⇒ 必要」の順番になると覚えておきましょう。

両方を満たす場合は必要十分条件

一方で必要条件と十分条件の両方を満たすことがあります。例として、以下の命題を考えてみましょう。

\(ab-a=b-1\)ならば、\(a=1\)または\(b=1\)

この命題は真でしょうか。それとも偽でしょうか。まず、pならばqを考えてみましょう。その前に、\(ab-a=b-1\)を因数分解する必要があります。以下のようになります。

\(ab-a=b-1\)

\(ab-a-b+1=0\)

\((a-1)(b-1)=0\)

このように因数分解すると、pならばqが真であるとわかります。\((a-1)(b-1)=0\)の答えは\(a=1\)または\(b=1\)です。そのため、この命題は十分条件を満たしています。

それでは、qならばpは真でしょうか。先ほどの命題について、pとqを反対にしてみましょう。以下のようになります。

\(a=1\)または\(b=1\)ならば、\(ab-a=b-1\)

前述のとおり、\(ab-a=b-1\)の答えは\(a=1\)または\(b=1\)です。そのため\(a=1\)または\(b=1\)の場合、必ず\(ab-a=b-1\)となります。このため、必要条件も満たしていることがわかります。必要条件と十分条件の両方を満たす場合、その命題は必要十分条件です。

なお「\(p⇒q\)」と「\(q⇒p\)」を満たす場合、集合Pと集合Qは等しいことを先に説明しました（P＝Q）。そのため必要十分条件を満たす命題では、pとqは同値になります。

また必要十分条件の場合、「pはqであるための必要十分条件である」と表現されます。先ほどの例題では、「\(ab-a=b-1\)は\(a=1\)または\(b=1\)であるための必要十分条件である」となります。または、「\(a=1\)または\(b=1\)は\(ab-a=b-1\)であるための必要十分条件である」と表現することもできます。