空間ベクトルの内積：公式や角度・面積の計算、垂直での内積

ベクトルの内積はベクトルの計算でひんぱんに利用されます。これは、空間ベクトルでの計算と同様です。

平面ベクトルと空間ベクトルでは、ベクトルの内積の概念は同じです。公式もほぼ同じであるため、平面ベクトルで内積を理解している場合、空間ベクトルでの内積を理解するのは簡単です。

空間ベクトルの内積は角度を利用することによって得られます。また、それぞれの成分を利用することで計算することもできます。他には、2つのベクトルが垂直の場合、内積はゼロになります。これらの性質は平面ベクトルと同様です。

それでは、空間ベクトルで内積を利用するにはどうすればいいのでしょうか。空間ベクトルでの内積の公式や角度・面積の計算方法、2つのベクトルが垂直となる場合の考え方を解説していきます。

1 空間ベクトルで内積を得る公式
- 1.1 空間ベクトルの内積の性質
- 1.2 \(x\)成分、\(y\)成分、\(z\)成分を利用する内積の出し方
2 2つのベクトルのなす角を利用し、面積を計算する
- 2.1 ベクトルが垂直の場合、内積はゼロになる
3 内積を用いて空間ベクトルの計算を行う

空間ベクトルで内積を得る公式

角度を利用してベクトルの内積を得たい場合、平面ベクトルも空間ベクトルも公式は同じです。2つのベクトルについて、cosθを用いて向きを同じにしたあと、長さをかけることによって内積を計算できます。

\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cosθ\)

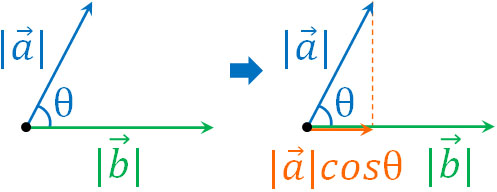
平面ベクトルであっても空間ベクトルであっても、角度を利用して内積を計算できる事実は同じです。

空間ベクトルの内積の性質

また内積の性質についても、平面ベクトルと空間ベクトルで同じです。

交換法則：\(\overrightarrow{a}·\overrightarrow{b}=\overrightarrow{b}·\overrightarrow{a}\)
分配法則：\(\overrightarrow{a}(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}·\overrightarrow{b}\)\(+\overrightarrow{a}·\overrightarrow{c}\)
実数倍：\(k\overrightarrow{a}(\overrightarrow{b})=\overrightarrow{a}(k\overrightarrow{b})\)\(=k(\overrightarrow{a}·\overrightarrow{b})\)
同じベクトル：\(\overrightarrow{a}·\overrightarrow{a}=|\overrightarrow{a}|^2\)

これらの性質を利用してベクトルの内積を計算しましょう。それでは、以下の問題の答えは何でしょうか。

辺の長さが1である正四面体OABCについて、\(\overrightarrow{OA}=\overrightarrow{a}\)、\(\overrightarrow{OB}=\overrightarrow{b}\)、\(\overrightarrow{OC}=\overrightarrow{c}\)であり、辺BC上に\(BD=\displaystyle\frac{1}{4}BC\)となる点Dを作ります。内積\(\overrightarrow{OA}·\overrightarrow{OD}\)を求めましょう。

ベクトルに関する計算問題では図を作らないと解くのが難しいため、必ず図を作りましょう。以下の図になります。

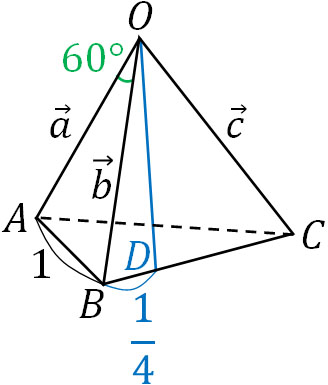
正四面体であるため、三角形の角度はすべて60°です。また、三角形の辺の長さはすべて1です。

なお内分点の公式を利用すると、\(\overrightarrow{OD}\)\(=\displaystyle\frac{3\overrightarrow{b}+\overrightarrow{c}}{1+3}\)\(=\displaystyle\frac{3\overrightarrow{b}+\overrightarrow{c}}{4}\)となります。そこで、以下のように計算しましょう。

\(\overrightarrow{OA}·\overrightarrow{OD}\)

\(=\overrightarrow{a}·\left(\displaystyle\frac{3\overrightarrow{b}+\overrightarrow{c}}{4}\right)\)

\(=\displaystyle\frac{3}{4}\overrightarrow{a}·\overrightarrow{b}+\displaystyle\frac{1}{4}\overrightarrow{a}·\overrightarrow{c}\)

そこで、\(\overrightarrow{a}·\overrightarrow{b}\)と\(\overrightarrow{a}·\overrightarrow{c}\)を計算しましょう。三角形の角度はすべて60°であり、辺の長さはすべて1なので以下のように計算できます。

\(\overrightarrow{a}·\overrightarrow{b}=1×1×cos60°=\displaystyle\frac{1}{2}\)
\(\overrightarrow{a}·\overrightarrow{c}=1×1×cos60°=\displaystyle\frac{1}{2}\)

こうして、以下のように計算できます。

\(\displaystyle\frac{3}{4}\overrightarrow{a}·\overrightarrow{b}+\displaystyle\frac{1}{4}\overrightarrow{a}·\overrightarrow{c}\)

\(=\displaystyle\frac{3}{4}×\displaystyle\frac{1}{2}+\displaystyle\frac{1}{4}×\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{1}{2}\)

こうして、ベクトルの内積を計算できました。

\(x\)成分、\(y\)成分、\(z\)成分を利用する内積の出し方

なおベクトルの内積を計算する方法はもう一つあります。角度を利用するのではなく、\(x\)成分、\(y\)成分、\(z\)成分を利用して内積を得るのです。

平面ベクトルでは、\(\overrightarrow{a}=(a_1,a_2)\)、\(\overrightarrow{b}=(b_1,b_2)\)について、以下の公式によって内積を計算できるとすでに学んでいると思います。

\(\overrightarrow{a}·\overrightarrow{b}=a_1b_1+a_2b_2\)

そこで空間ベクトルについても、同じ方法で内積を計算しましょう。\(\overrightarrow{a}=(a_1,a_2,a_3)\)、\(\overrightarrow{b}=(b_1,b_2,b_3)\)のとき、内積の公式は以下になります。

\(\overrightarrow{a}·\overrightarrow{b}=a_1b_1+a_2b_2+a_3b_3\)

空間ベクトルでは\(z\)成分が増えるため、\(a_3b_3\)を考慮する必要があります。いずれにしても、内積を計算する公式は平面ベクトルでも空間ベクトルでもほぼ同じです。

2つのベクトルのなす角を利用し、面積を計算する

それでは、ベクトルの内積を利用することによって応用問題を解けるようになりましょう。空間ベクトルで出題される問題の一つに面積の計算があります。以下の図では、\(a\)にsinθをかけることでたての長さを得ることができます。

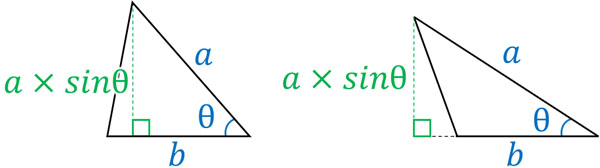
そのため、三角形の面積\(S\)を以下の公式によって得ることができます。

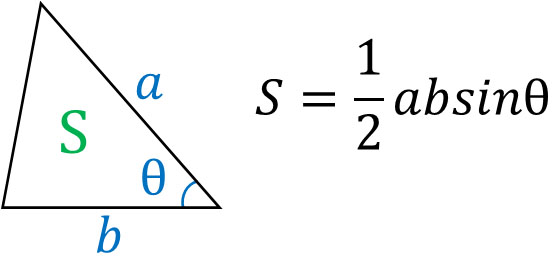
それでは、以下の問題の答えは何でしょうか。

A\((1,2,3)\)、B\((-1,0,3)\)、C\((1,2,-3)\)を頂点とする三角形について、三角形の面積を求めましょう。

空間ベクトルではあっても、三角形であれば辺の長さと角度を計算できます。そこで、ベクトルの内積を利用して計算しましょう。以下の図を作ります。

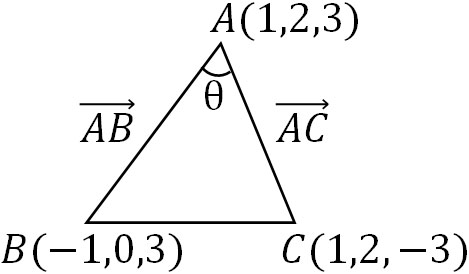
まず、\(\overrightarrow{AB}\)の長さを計算しましょう。

\(|\overrightarrow{AB}|=\)\(\sqrt{(-1-1)^2+(0-2)^2+(3-3)^2}\)

\(|\overrightarrow{AB}|=\sqrt{8}\)

\(|\overrightarrow{AB}|=2\sqrt{2}\)

次に、\(\overrightarrow{AC}\)の長さを計算します。

\(|\overrightarrow{AC}|=\)\(\sqrt{(1-1)^2+(2-2)^2+(-3-3)^2}\)

\(|\overrightarrow{AC}|=\sqrt{36}\)

\(|\overrightarrow{AC}|=6\)

辺の長さがわかったため、sinθを得ることができれば、三角形の面積がわかります。そこでベクトルの内積を利用してsinθを計算しましょう。\(|\overrightarrow{AB}|=(-2,-2,0)\)、\(|\overrightarrow{AC}|=(0,0,-6)\)であるため、\(\overrightarrow{AB}·\overrightarrow{AC}\)は以下のように計算できます。

\(\overrightarrow{AB}·\overrightarrow{AC}=-2×0+(-2)×0\)\(+0×(-6)\)

\(\overrightarrow{AB}·\overrightarrow{AC}=0\)

そのため、以下のようになります。

\(\overrightarrow{AB}·\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cosθ\)

\(0=2\sqrt{2}×6×cosθ\)

\(cosθ=0\)

\(cosθ=0\)であるため、\(sinθ=1\)です。\(sin^2θ+cos^2θ=1\)だからです。そのため、以下のように三角形の面積\(S\)を計算しましょう。

\(S=\displaystyle\frac{1}{2}×2\sqrt{2}×6×sinθ\)

\(S=6\sqrt{2}\)

なお教科書によっては、「ベクトルを用いて三角形の面積を得る公式」を記していることがあります。以下が公式です。

\(S=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}·\overrightarrow{b})^2}\)

ただ、この公式を覚えてはいけません。そうではなく、内積や辺の長さ、sinθを利用して計算しましょう。そうすれば、公式を覚えることなく三角形の面積を計算できます。

ベクトルが垂直の場合、内積はゼロになる

なおベクトルの内積でひんぱんに利用される性質として、2つのベクトルの垂直関係があります。2つのベクトルが垂直の場合、内積はゼロになります。

先ほどの面積の計算では、\(\overrightarrow{AB}·\overrightarrow{AC}=0\)とわかりました。これは、2つのベクトルが垂直であることを意味しています。垂直だと\(θ=90°\)、つまり\(cosθ=0\)となるため、内積は必ずゼロになります。

そこで、この性質を利用して問題を解けるようになりましょう。以下の問題の答えは何でしょうか。

\(\overrightarrow{a}=(2,1,3)\)、\(\overrightarrow{b}=(1,-1,0)\)の両方に垂直な単位ベクトル\(\overrightarrow{e}\)を求めましょう。

まず、\(\overrightarrow{e}=(x,y,z)\)とします。\(\overrightarrow{e}\)は単位ベクトルであるため、以下の式が成り立ちます。

\(x^2+y^2+z^2=1\)

また2つのベクトルに対して垂直の関係になる必要があるため、以下の関係が成り立ちます。

\(\overrightarrow{a}·\overrightarrow{e}=2x+y+3z=0\)
\(\overrightarrow{b}·\overrightarrow{e}=x-y=0\)

\(x-y=0\)より、\(x=y\)です。そこで、以下のように計算しましょう。

\(2x+y+3z=0\)

\(2x+x+3z=0\)

\(3x=-3z\)

\(z=-x\)

次に、\(x^2+y^2+z^2=0\)へ代入しましょう。

\(x^2+y^2+z^2=1\)

\(x^2+x^2+(-x)^2=1\)

\(x^2=\displaystyle\frac{1}{3}\)

\(x=±\displaystyle\frac{1}{3}\)

\(x=±\displaystyle\frac{1}{\sqrt{3}}\)であるため、以下の2つが答えであるとわかります。

\(\overrightarrow{e}=\displaystyle\frac{1}{\sqrt{3}},\displaystyle\frac{1}{\sqrt{3}},-\displaystyle\frac{1}{\sqrt{3}}\)
\(\overrightarrow{e}=-\displaystyle\frac{1}{\sqrt{3}},-\displaystyle\frac{1}{\sqrt{3}},\displaystyle\frac{1}{\sqrt{3}}\)

こうして、垂直とベクトルの内積を利用することによって単位ベクトル\(\overrightarrow{e}\)を得ることができました。