力学では、力学的エネルギー保存則を習います。力のつり合いを基準とすれば、力学的エネルギー保存則が成り立ちます。
一方、単振動のエネルギー保存則では位置エネルギー\(mgh\)を省きます。そのため、多くの人が「なぜ位置エネルギーを無視するのか?」と混乱します。実際には位置エネルギーを無視しておらず、考慮しているのですが、多くの人が疑問に思うのです。
力のつり合いでの力学的エネルギー保存則と単振動のエネルギー保存則は概念が異なります。そこで、両者の違いや位置エネルギー(\(mgh\))を省ける理由を理解しなければいけません。
単振動では、エネルギー保存則を利用して計算する場面が多いです。そこで、どのように単振動でエネルギー保存則を利用し、計算問題を解けばいいのか解説していきます。
もくじ
単振動での力学的エネルギー保存則
ばねが振動するとき、力学的エネルギー保存則が成り立ちます。当然、単振動のときについても力学的エネルギー保存則は有効です。
運動エネルギー、位置エネルギー、弾性エネルギーには以下の関係が成り立ちます。
- \(\displaystyle\frac{1}{2}mv^2+mgh+\displaystyle\frac{1}{2}kx^2=\)一定 – ①
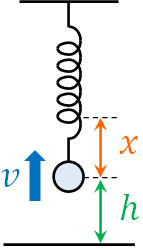
力学的エネルギー保存則は既に理解していると思います。物体の速さ\(v\)や高さ\(h\)、自然長からの長さ\(x\)を足すと、常に一定になります。
一方で単振動では、以下のエネルギー保存則が成り立ちます。
- \(\displaystyle\frac{1}{2}mv^2+\displaystyle\frac{1}{2}kx^2=\)一定 – ②
先ほどの式に対して、位置エネルギーに相当する\(mgh\)が消えています。単振動では、高さ\(h\)を利用せずに力学的エネルギー保存則を利用して計算することができます。
単振動では位置エネルギーは無視できる?
位置エネルギーに相当する\(mgh\)を無視するため、単振動のエネルギー保存則を学ぶときに多くの人が混乱します。重要なのは、「①の式にある\(\displaystyle\frac{1}{2}kx^2\)と②の式にある\(\displaystyle\frac{1}{2}kx^2\)は別物」という事実です。
①の\(x\)は自然長からの距離です。一方で②では自然長のときを\(x=0\)にするのではなく、重りを加えた後に静止した位置を\(x=0\)にします。単振動では力がつり合って静止している場所を基準にする必要があり、自然長からの距離を基準にしていません。
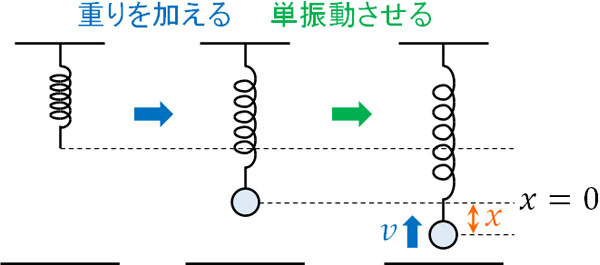
②の式に存在する\(\displaystyle\frac{1}{2}kx^2\)は単振動による位置エネルギーであり、重力による位置エネルギーと弾性力によるエネルギーを含んでいるのです。②の式では、重りをつるして静止している状態を基準にしていることを理解しましょう。
計算により、位置エネルギーを省略できる理由を学ぶ
ここまでの内容をまとめると、一般的な力学的エネルギー保存則と単振動でのエネルギー保存則では、以下の違いがあります。

それでは、単振動のエネルギー保存則を導き出してみましょう。
まず、ばねの自然長から重りをつるし、静止している場面を考えます。このとき、重力とばねの弾性力がつり合っているため、以下の式が成り立ちます(自然長からの伸びを\(h’\)とします)。
- \(mg=kh’\)
重力による影響は\(F=mg\)であり、ばねの弾性力は\(F=kh’\)なので、このつり合いの式は問題なく理解できると思います。
単振動しているときの力学的エネルギー保存則
次に、この状態からばねを振動させます。単振動させる場合、下図のように自然長からの距離は\(h’+x\)となります。また高さが低くなっているため、位置エネルギーの変化は\(-mg(h’+x)\)です。
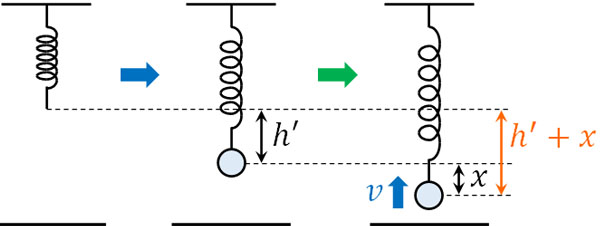
ばねがもつ弾性エネルギーについては、自然長からの距離は\(h’+x\)です。そのため、ばねがもつ弾性エネルギーは\(\displaystyle\frac{1}{2}k(h’+x)^2\)です。これに運動エネルギーとして\(\displaystyle\frac{1}{2}mv^2\)が加わります。
つまり単振動しているとき、力学的エネルギー保存則を利用して以下のように表すことができます。\(\)
- \(-mg(h’+x)\)\(+\displaystyle\frac{1}{2}k(h’+x)^2\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
力学的エネルギー保存則を利用して単振動を計算する場合、このように複雑な式を作ることになります。
力学的エネルギー保存則を単振動のエネルギー保存則に変える
それでは、力学的エネルギー保存則の式を単振動のエネルギー保存則に変えましょう。先ほど説明した通り、\(mg=kh’\)です。そこで、以下の式に\(mg=kh’\)を代入して計算しましょう。
\(-mg(h’+x)\)\(+\displaystyle\frac{1}{2}k(h’+x)^2\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
\(-kh'(h’+x)\)\(+\displaystyle\frac{1}{2}k(h’+x)^2\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
\(-kh’^2-kh’x\)\(+\displaystyle\frac{1}{2}k(h’^2+2h’x+x^2)\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
\(-kh’^2\)\(+\displaystyle\frac{1}{2}k(h’^2+x^2)\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
\(-\displaystyle\frac{1}{2}kh’^2+\displaystyle\frac{1}{2}kx^2\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
このとき、ばね定数\(k\)は一定であり、自然長からの伸び\(h’\)も一定です。つまり、\(-\displaystyle\frac{1}{2}kh’^2\)は定数であり、常に一定の値となります。値に変化がない定数であるため、\(-\displaystyle\frac{1}{2}kh’^2\)を右辺に移動させましょう。
なお\(-\displaystyle\frac{1}{2}kh’^2\)は定数であるため、\(-\displaystyle\frac{1}{2}kh’^2\)を右辺に移動させても計算結果は常に一定(同じ値)になります。つまり、以下の式となります。

こうして、以下の単振動のエネルギー保存則を導き出すことができました。
- \(\displaystyle\frac{1}{2}kx^2\)\(+\displaystyle\frac{1}{2}mv^2=\)一定
単振動での\(\displaystyle\frac{1}{2}kx^2\)は重力による位置エネルギーを含んでいます。位置エネルギーである\(mg(h’+x)\)を省いているわけではありません。
多くの教科書はここまで解説した内容を説明していないため、単振動を学ぶほとんどの人が混乱します。そこで、なぜ単振動では位置エネルギーの記載を省略しているのか理解しましょう。
単振動のエネルギー保存則を利用する練習問題
エネルギー保存則を利用して単振動の問題を解くとき、一般的な力学的エネルギー保存則を利用してもいいですし、単振動のエネルギー保存則を利用してもいいです。
先ほど、力学的エネルギー保存則を利用して単振動のエネルギー保存則を導き出しました。つまり、どちらを利用しても同じ答えを得ることができます。
ただ単振動のエネルギー保存則では高さを考慮する必要がないため、一般的な力学的エネルギー保存則を利用するよりも圧倒的に計算が楽になります。そのため単振動の計算問題では、単振動のエネルギー保存則を利用しましょう。
それでは、以下の問題の答えは何でしょうか。
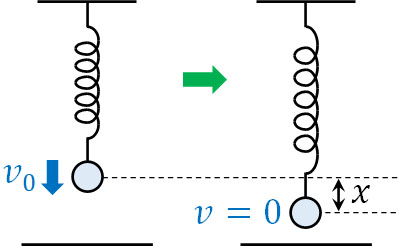
- ばね定数\(k\)のばねに質量\(m\)の重りをつけた後、初速\(v_0\)を加えるとばねは単振動を開始しました。単振動の振幅を求めましょう。
振幅を求めるというのは、単振動でのばねの伸び(または縮み)が最大になるときを計算すればいいとわかります。また振幅が最大になるとき、速度はゼロです。つまり、運動エネルギーがすべて弾性エネルギーへと変換されます。
そこで、以下の式を作りましょう。
\(\displaystyle\frac{1}{2}mv_0^2=\displaystyle\frac{1}{2}kx^2\)
\(x^2=\displaystyle\frac{mv_0^2}{k}\)
\(x=v_0\sqrt{\displaystyle\frac{m}{k}}\) (\(x>0\))
こうして、振幅は\(x=v_0\sqrt{\displaystyle\frac{m}{k}}\)になるとわかりました。
なお、力学的エネルギー保存則を利用することで\(x=v_0\sqrt{\displaystyle\frac{m}{k}}\)を得ることもできます。ただ計算式が大変になるため、単振動のエネルギー保存則を利用しましょう。
単振動のエネルギー保存則では高さを省略できる
単振動では、一般的な力学的エネルギー保存則に加えて、単振動のエネルギー保存則を利用できます。この場合、位置エネルギーが既に考慮されているため、高さを考えることなくエネルギー保存則を利用できます。
ただ多くの教科書では、単振動のエネルギー保存則で\(mgh\)を省略できる理由を述べていません。そのため、ほとんどの人が混乱します。
力学的エネルギー保存則と単振動のエネルギー保存則では、\(x\)の意味が異なります。力学的エネルギー保存則では、自然長からの距離が\(x\)です。一方で単振動のエネルギー保存則では、振動中心からの距離が\(x\)です。なお単振動のエネルギー保存則は重力による位置エネルギーを考慮しています。
物理で単振動の計算をするとき、なぜ単振動のエネルギー保存則では位置エネルギーの計算を無視できるのか学びましょう。これにより、単振動のエネルギー保存則で何を計算しているのか理解できます。






