3群以上を含む標本を検定するとき、分散分析(ANOVA)が利用されます。分散分析には一元配置分散分析や二元配置分散分析があります。ただ母集団が正規分布していない場合、その他の方法を利用しなければいけません。
このとき、母集団が正規分布していなくても利用できる検定法がフリードマン検定です。二つの因子を含む多群の標本について、あらゆるデータで利用できるのです。
それでは、フリードマン検定はどのように利用するのでしょうか。フリードマン検定ではカイ二乗分布を使います。そこで、フリードマン検定で利用する公式の意味や検定の概念を学びましょう。
多群の検定では概念が難しいです。また、ほかの分散分析との違いを理解しなければいけません。そこで、どのようにフリードマン検定をすればいいのか解説していきます。
もくじ
因子が二つで対応のある多群を検定するノンパラメトリック検定
分散分析には一元配置分散分析や二元配置分散分析があります。こうした分散分析では、前述の通り母集団が正規分布している必要があります。つまり、パラメトリック検定になります。
また一元配置分散分析や二元配置分散分析では、データが等分散でなければいけません。等分散の場合、グラフの形が同じになります。
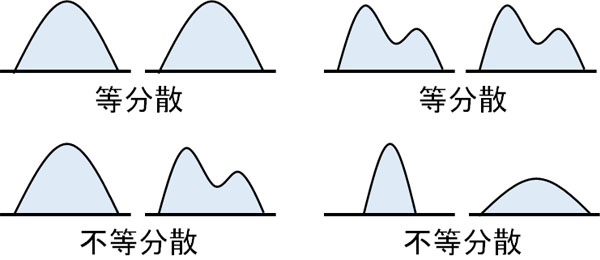
3群以上をもつ標本について、等分散かどうかを確認する方法にバートレット検定があります。ただバートレット検定で「等分散ではない」とわかった場合、一元配置分散分析や二元配置分散分析を利用することはできません。その場合、ノンパラメトリック検定であるフリードマン検定が利用されます。
クラスカル・ウォリス検定との違いは何か
なお多群の検定をするとき、母集団が正規分布していなくても利用できる検定法としては、フリードマン検定だけでなくクラスカル・ウォリス検定もあります。この違いとしては何があるのでしょうか。
それぞれの違いは以下のように考えましょう。
- 一元配置分散分析に対応(因子が一つで、対応のない検定):クラスカル・ウォリス検定
- 二元配置分散分析に対応(因子が二つで、対応のある検定):フリードマン検定
つまり因子が一つ(対応なし)なのか、それとも因子が二つ(対応あり)なのかで考えましょう。
例えば「製品Aの性能を調べる」という場合、一つの因子を用いて調査することになります。一方で「男女ごとに体重を調べる」という場合、男女と体重という二つの因子を利用することになります。クラスカル・ウォリス検定とフリードマン検定は大きく中身が異なるのです。
順位和Rを利用し、行または列で有意差を確認する
それでは、実際にフリードマン検定をするときはどのように検定するのでしょうか。これについて、「二つの因子を配置したとき、行と列のどちらに着目したいのか」を決めましょう。このとき行に着目する場合について、差があるかどうかを検定できます。また、列に着目する場合についても、差があるかどうかを検定できます。
一方だけを検定してもいいですし、両方を検定してもいいです。例えばテストを行い、以下のような結果を得られたとします。
| Aさん | Bさん | Cさん | Dさん | Eさん | |
| 数学 | 8 | 5 | 7 | 10 | 4 |
| 物理 | 3 | 1 | 3 | 7 | 4 |
| 化学 | 6 | 3 | 2 | 5 | 1 |
| 歴史 | 7 | 6 | 5 | 9 | 2 |
この場合、行に着目すると「教科ごとに難易度の違いがあるか」を検定できます。一方で列に着目すると「人によって学力に差があるか」を検定できます。いずれにしても、行と列のどちらに着目して検定したいのか決めましょう。
・行の要因を調べたい場合
フリードマン検定では、行または列に着目して順位をつけます。例えば行(教科による難易度)に着目する場合、列で順位をつけます。列で順位をつければ、「どの教科の点数が高いのか(または低いのか)」が人ごとにわかります。
その後、すべての順位を横で足しましょう。順位を足すことで得られる値を順位和Rといいます。
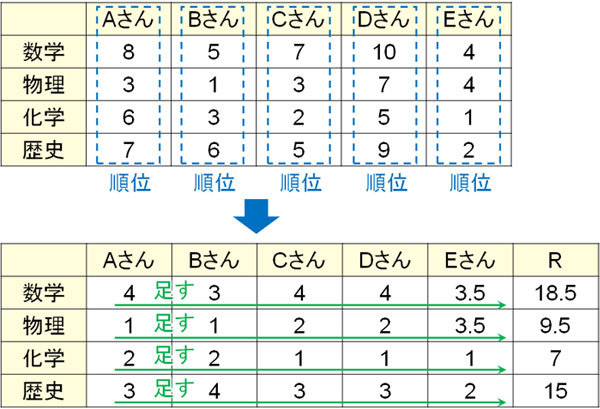
なお同じ値の場合、順位の平均値を利用しましょう。こうして順位和Rを計算し、有意水準とp値を比較することによって有意差を検証します。
・列の要因を調べたい場合
一方で列に着目する場合(人による学力の差)、どのように順位和Rを計算すればいいのでしょうか。この場合、行ごとに順位を出しましょう。行によって順位を出すことにより、「誰が高得点なのか」を教科別に出すことができます。
その後、すべての順位をたてで計算しましょう。
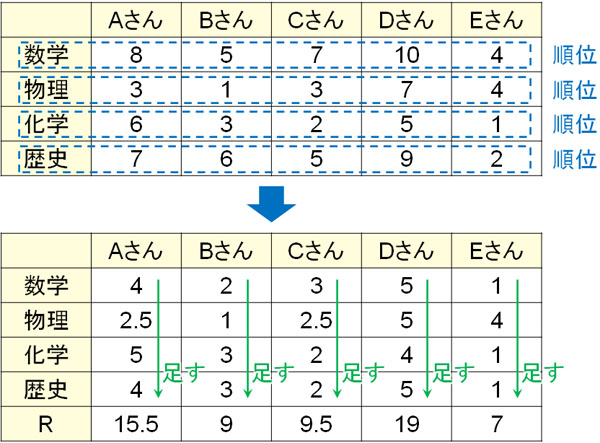
教科別にランキングを出した後、列ごと(人別)に足すことによって、学力に差があるかどうか判定することができます。
フリードマン検定を行うときの検定の概念
差がない場合、すべての行(または列)について、順位和Rは同じ値になります。一方、順位和Rに違いがある場合(差がある場合)、行(または列)によって違いがあるといえます。例えば列に違いがある(人によって学力に違いがある)という場合、点数が低い人は順位和Rが低くなり、成績の良い人は順位和Rが高くなります。
このように順位和Rを比べて違いがある場合、差があると判断するのです。なおグラフにすると、差があるときと差がないときは以下のようになります。
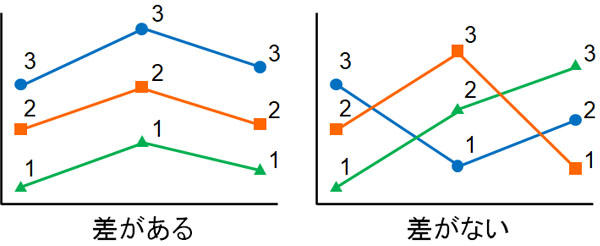
差がある場合、折れ線グラフの横軸(青線、オレンジ線、緑線)の順位を足すと、順位和Rは異なります。一方で差がない場合、順位和Rは同じです。フリードマン検定では、このような概念によって差があるかどうかを検定します。
なおフリードマン検定はカイ二乗分布に従います。差がある場合、カイ二乗値は大きくなります。一方で差がない場合、カイ二乗値は0になります。
フリードマン検定で利用する公式の詳細
それでは、フリードマン検定を利用するときはどのような公式を使うのでしょうか。前述の通り、フリードマン検定では順位和Rを活用します。それに加えて、群数\(k\)とデータ数\(n\)を利用しましょう。
行と列について、群数\(k\)とデータ数\(n\)は以下のようになります。
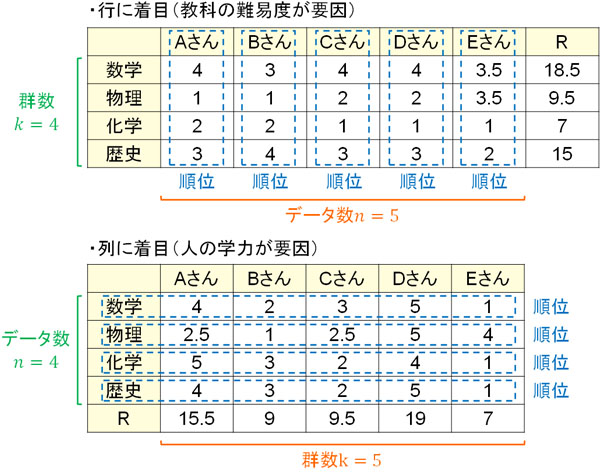
このとき、フリードマン検定で利用される公式は以下になります。
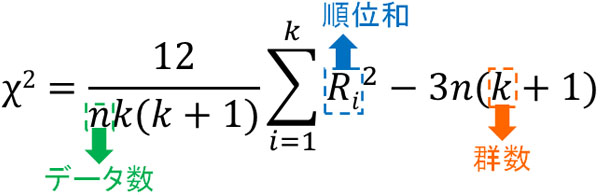
なお、この公式を分解すると以下のようになります。
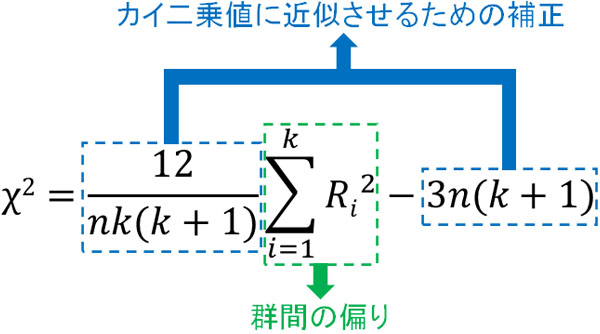
公式を覚える必要はありません。ただ、公式が何を意味しているのか理解しましょう。
カイ二乗分布を利用し、確率を計算する
それでは、実際にカイ二乗分布を利用して確率の計算をしてみましょう。先ほどの表について行に着目し、教科によって難易度に違いがあるかどうかを検定しましょう。
このときの帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:教科によって難易度に差はない
- 対立仮説:教科によって難易度に差がある
そこで、順位和Rを利用してカイ二乗値を以下のように計算しましょう。

こうして、公式を利用することでχ2値は9.78とわかりました。
フリードマン検定を利用し、有意差を確認する
次に、有意水準0.05(5%)となる値を探しましょう。フリードマン検定では、自由度は群数から1を引きます。今回の場合であれば、群数は4です。そのため、自由度は\(4-1=3\)です。
自由度3のカイ二乗分布に従うとき、0.05となるカイ二乗値を統計学の教科書から探すと、7.815であるとわかります。つまり7.815よりもカイ二乗値が大きい場合、5%以下で起こる稀な現象が発生しているといえます。
そこで有意水準とp値を確認すると、計算したカイ二乗値は9.78であり、7.815よりも値が大きいです。そのため帰無仮説を棄却でき、対立仮説を採用しましょう。つまり、教科によって難易度に違いがあるといえます。
なお行ではなく、列に着目してフリードマン検定をすることも可能です。この場合、順位和Rを利用して、同じ方法によって有意差を確認しましょう。
また前述の通り、フリードマン検定によって差があるとわかっても、どの群で差があるのかを調べることはできません。そこで具体的にどのグループ間で差があるのか調べたい場合、2群検定と多重比較法を利用して、さらなる検定が必要です。
対応のある2つの群を調べるとき、ノンパラメトリック検定ではウィルコクソンの符号順位検定を利用します。そのため詳しく調べたい場合、ウィルコクソンの符号順位検定と多重比較法を利用しましょう。
フリードマン検定の概念を理解し、多群の検定を行う
多群の検定をしたいとき、フリードマン検定が有効です。二つの因子をもつ標本について、ノンパラメトリック検定をしたい場合はフリードマン検定を利用しましょう。
順位を利用して検定するため、外れ値が含まれていたとしても検定することができます。母集団が正規分布しているかどうか不明であったり、データが等分散でなかったりする場合はフリードマン検定が利用されます。
フリードマン検定では順位和Rを使います。公式を利用してカイ二乗値を計算し、有意差があるかどうかを判断しましょう。
公式を覚える必要はないものの、理論を学ぶ必要があります。フリードマン検定によって何を確認しているのかを理解し、差があるかどうかを判定しましょう。






