複数の群を含む標本を検定したいとき、クラスカル・ウォリス検定(Kruskal-Wallis検定)を利用します。分散分析と呼ばれており、それぞれの群で差があるかどうかを調べるのです。
クラスカル・ウォリス検定はノンパラメトリック検定の一つです。つまり、母集団が正規分布するかどうかに関係なく利用できます。特に一元配置分散分析による検定ができない場合、クラスカル・ウォリス検定が採用されます。
それでは、どのようにクラスカル・ウォリス検定を利用すればいいのでしょうか。また、検定するときの理論はどのようになっているのでしょうか。
統計学を学んで検定をするとき、事前に理論や公式の意味を学びましょう。これにより、検定結果の意味を理解できるようになります。
もくじ
因子が一つの場合のノンパラメトリック検定
分散分析(ANOVA)の中でも、因子が一つの場合に頻繁に利用される手法が一元配置分散分析 (One Way ANOVA) です。
ただ一元配置分散分析を利用するためには、母集団が正規分布している必要があります。そのため母集団が正規分布していない場合、一元配置分散分析を利用できません。
さらには、一元配置分散分析を利用するにはデータが等分散でなければいけません。3群以上を含む標本で等分散かどうかを調べる手法にバートレット検定があります。そのためバートレット検定を利用し、不等分散とわかった場合、一元配置分散分析を利用してはいけません。
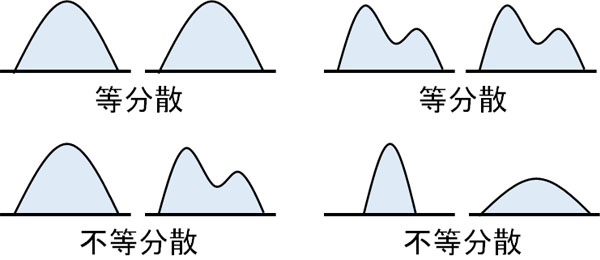
そうしたとき、クラスカル・ウォリス検定を利用します。一元配置分散分析はパラメトリック検定です。一方でクラスカル・ウォリス検定については、母集団の正規分布や等分散に関係なく利用できるノンパラメトリック検定です。
そこで因子が一つであり、一元配置分散分析を利用できない場合、クラスカル・ウォリス検定を利用して検定しましょう。なお一元配置分散分析では対応のないデータを利用します。そのためクラスカル・ウォリス検定についても、対応のない3群以上の標本で利用されます。
順位を利用し、差があるかどうかを検定する
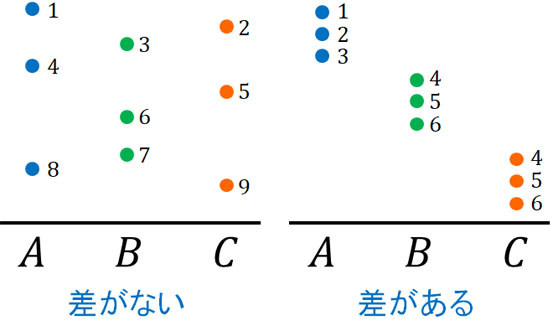
それでは、クラスカル・ウォリス検定ではどのようにして差があるかどうかを調べるのでしょうか。クラスカル・ウォリス検定では順位を利用します。つまりデータを順番に並べ、順番を数えるのです。順番を利用して検定するため、外れ値があっても差があるかどうかを調べることができるのです。
このときそれぞれの群にさまざまな順位が含まれる場合、差がないと判断します。一方で群によって順番に明確な傾向がある場合、差があると判断します。
クラスカル・ウォリス検定では、統計量Hを利用することによって差があるかどうかを確認します。
統計量Hが0に近い場合、差があるとはいえません。一方で統計量Hが大きい値の場合、差があると判断します。グループ間の偏りが大きいほど、統計量Hの値は大きくなるのです。
クラスカル・ウォリス検定と統計量Hの関係で学ぶ検定の概念
それでは、 クラスカル・ウォリス検定で利用される統計量Hはどのように求めればいいのでしょうか。前述の通り、すべてのデータについて順位をつけます。つまり、小さい順に番号を振っていきます。
例えば、以下のような順位になります。

一方で値が同じ場合、平均の順位を利用しましょう。以下のようになります。
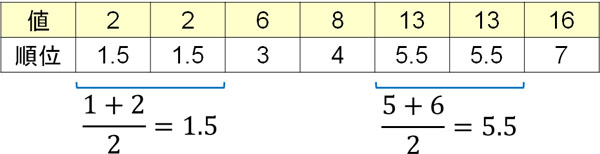
このようにして、クラスカル・ウォリス検定ではデータごとに順位をつけていきます。
なおすべての分散分析に共通しますが、クラスカル・ウォリス検定を利用して「差がある」とわかっても、どのグループ間で差があるのか判断することはできません。そのため有意差が出た後、どの群で差があるのか調べる必要があります。
なお対応のないデータの場合、2群の検定が可能なノンパラメトリック検定としてマン・ホイットニーのU検定(ウィルコクソンの順位和検定)を利用します。そのためクラスカル・ウォリス検定でp値と有意水準を比較して有意差を得られたのであれば、マン・ホイットニーのU検定を利用して調べましょう。
群ごとに順位の合計Rを求め、公式を利用して統計量Hを計算する
それでは、実際に統計量Hを求めてみましょう。このとき、群ごとの順位の合計を\(R\)、サンプル数を\(N\)、各群のデータ数を\(n\)とするとき、統計量Hは以下の公式によって得ることができます。
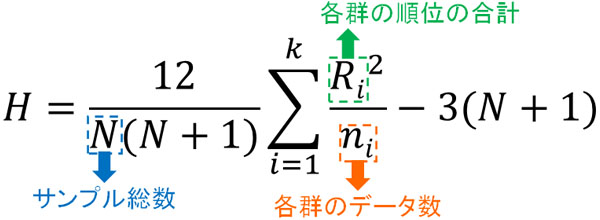
この公式を覚える必要はなく、「この公式に数値を代入すれば統計量Hを求めることができる」と理解できれば問題ありません。
なおこの公式を分解すると以下のようになります。
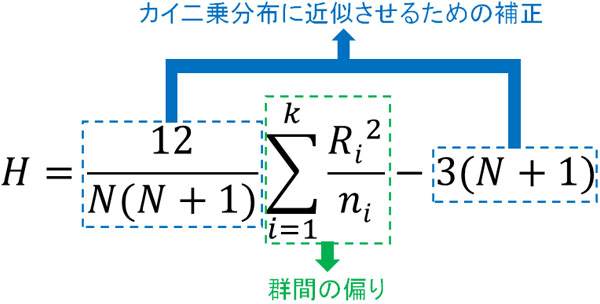
クラスカル・ウォリス検定ではカイ二乗分布を利用することによって確率を計算します。サンプル数が多い場合、カイ二乗分布に近似できるため、そのための補正をするというわけです。
この公式によって統計量Hを計算でき、有意差を確認できることを数学者が考えてくれたため、私たちはこれを利用しましょう。
小標本・大標本によって検定方法を分ける
なお実際に統計量Hを計算するとき、群の数やサンプル数によって検定方法を分けましょう。具体的には、以下のように考えます。
・小標本の場合
群の数kが3であり、かつ全サンプル数Nが17以下のとき、クラスカル・ウォリス検定表を利用して有意水準と比較します。統計学の教科書に記されているクラスカル・ウォリス検定表には、各群に含まれているデータ数に応じて、有意水準が0.05(または0.01)となる統計量Hが記されています。
そこで有意水準0.05となる統計量Hに対して、計算した統計量Hが大きいのか、それとも小さいのかを確認しましょう。計算した統計量Hが有意水準よりも大きい場合、帰無仮説を棄却できます。
・大標本の場合
一方で群の数kが4以上であったり、全サンプル数が18以上であったりするとき、統計量Hは近似的にカイ二乗分布に従います。このときの自由度は「群の数から1を引いた値」です。そこで自由度を利用し、有意水準0.05となるカイ二乗値と比較しましょう。
統計量Hやカイ二乗分布を利用して確率を計算する
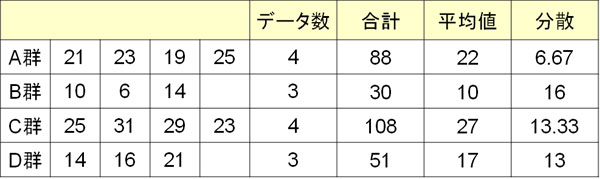
それでは、実際に統計量Hを利用してクラスカル・ウォリス検定をしてみましょう。例えば以下のとき、データ間に差があるといえるでしょうか。
帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:それぞれの群に差はない
- 対立仮説:それぞれの群に差がある
まず、順位ごとに並べてみましょう。その後、群ごとに合計Rを計算します。以下のような表になります。
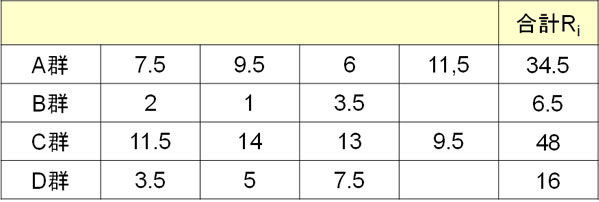
なお、データ総数(合計のサンプル数)Nは14です。そこで、以下のように統計量Hを計算しましょう。
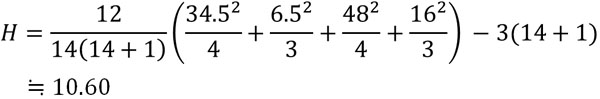
こうして、統計量Hは10.60であることがわかりました。この値と「有意水準が0.05(5%)となるカイ二乗値」を比較しましょう。群の数は4つであるため、統計量Hがカイ二乗分布に従うと考えるのです。
群の数は4つであるため、自由度\((4-1=)3\)のカイ二乗分布に従います。自由度3のとき、0.05となるカイ二乗値は7.815です。
統計量Hは10.60であるため、有意水準0.05となる7.815と比べて大きい数字です。つまり、5%以下の確率で起こる稀な現象が起こっていると考えることができます。そのため帰無仮説を棄却し、対立仮説を採用しましょう。つまり、グループ間に差があると結論付けることができます。
なお前述の通り、具体的にどのグループ間で差があるのかはわかりません。そのため有意差がある場合、次は2群検定と多重比較法を利用して、どの群に差があるのか調べます。対応のないデータではマン・ホイットニーのU検定を利用し、どのグループ間で差があるのか調査するのです。
3群以上をもつ標本を調べるクラスカル・ウォリス検定
分散分析で重要なパラメトリック検定が一元配置分散分析です。このとき、一元配置分散分析のノンパラメトリック検定版がクラスカル・ウォリス検定です。3群以上をもつ標本について、母集団の正規分布が不明であったり、バートレット検定で等分散でないと判断できたりする場合、クラスカル・ウォリス検定を利用しましょう。
順位を利用することによって検定するのがクラスカル・ウォリス検定です。順位を利用するため、外れ値があっても検定することができるのです。
そこで、統計量Hの意味を理解しましょう。統計量Hは近似的にカイ二乗分布に従います。統計量Hを利用して、有意水準と比べることで確率を計算しましょう。
利用する公式は難しいです。ただ公式を覚えるのではなく、どのような計算をしているのか理論を学びましょう。そうすれば、クラスカル・ウォリス検定を利用して検定できるようになります。






