分散分析を学ぶとき、必ず理解しなければいけないのが二元配置分散分析(Two-way ANOVA)です。因子が二つであり、3群以上をもつ標本であれば、二元配置分散分析を利用して検定をしましょう。
一元配置分散分析と原理は同じであるため、一元配置分散分析を学んでいる場合、二元配置分散分析を理解できます。計算方法は異なるものの、利用する公式は似ているのです。
ただ二元配置分散分析では、繰り返しなしと繰り返しありのケースを考える必要があります。2つの因子による効果を交互作用と呼びます。二元配置分散分析では交互作用を考慮しなければいけないことがあります。
一元配置分散分析に加えて、二元配置分散分析では新たな概念を学ばなければいけません。そこで二元配置分散分析を利用して多群の検定をするときについて、公式の意味や検定の方法、交互作用の意味を解説していきます。
もくじ
2つの因子をもち、3群以上の標本に対するパラメトリック検定
一元配置分散分析(One-way ANOVA)では一つの因子をもつ標本に対して利用できます。一方で二元配置分散分析(Two-way ANOVA)では、二つの因子をもつ標本に対して利用します。
例えば「薬Aの溶けるスピードを調べる」という場合、一つの因子について調査します。一方で「男女と体重の関係を調べる」という場合、性別と体重という二つの因子について調査します。
実際のところ、二つの因子が関係しているケースがほとんどです。そのため、二元配置分散分析は頻繁に利用されるのです。また二元配置分散分析は3群以上をもつ標本で活用されます。例えば、以下の標本は二元配置分散分析を利用して検定をします。
- 4人について、テストをすると以下の結果を得ることができました。
| Aさん | Bさん | Cさん | Dさん | |
| 数学 | 8 | 5 | 7 | 10 |
| 物理 | 3 | 1 | 3 | 7 |
| 化学 | 6 | 3 | 2 | 5 |
この場合、人間(Aさん、Bさん、Cさん、Dさん)と教科(数学、物理、化学)のように、二つの因子があります。また標本には複数の群があるため、二元配置分散分析が有効です。
対応のある二標本t検定に相当し、事前のバートレット検定が必要
なお二元配置分散分析というのは、t検定でいう「対応のある二標本t検定」に相当します。対応のある二標本t検定では、2群について差があるかどうかを判定します。一方で二元配置分散分析では、対応のある群について、多群の検定をするのです。
二元配置分散分析はパラメトリック検定に該当し、母集団が正規分布していることが前提となります。対応のある標本について、標本が多群の場合は二元配置分散分析を行うと考えましょう。
また一元配置分散分析やスチューデントのt検定でも共通しますが、二元配置分散分析をするためにはデータが等分散でなければいけません。つまり、データの形が同じである必要があるのです。
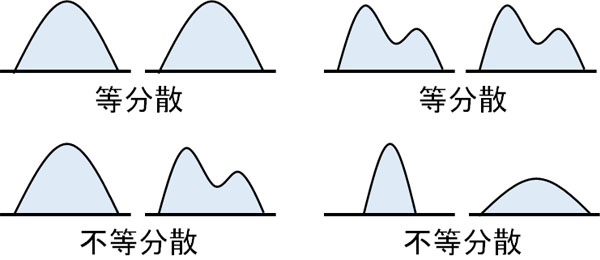
等分散かどうかを判断する方法がバートレット検定です。そのため二元配置分散分析を行う前、必ずバートレット検定をすることによって等分散かどうかを確認する必要があります。
二元配置分散分析により、行と列で2つの結果を得られる
それでは、なぜ二元配置分散分析が「対応のある二標本t検定」に相当するのでしょうか。まず二元配置分散分析では、行と列を別々に着目し、2つの結果を得ることができます。
先ほどの事例であれば、人間(Aさん、Bさん、Cさん、Dさん)と教科(数学、物理、化学)の2つの因子があります。このとき、人間に着目するのか、それとも教科に着目するのかによって以下の2通りの結果を得られます。
- 人間(Aさん、Bさん、Cさん、Dさん)によってテスト結果に差があるか
- 教科によって難しさに差があるか
そのためt検定や一元配置分散分析とは異なり、二元配置分散分析では答えが2つあることを理解しましょう。
この場合、必ず対応のある標本となります。例えば教科に着目する場合、「同じ人間が複数教科のテストを受け、テストの難しさに違いがあるのか」を確認することになります。同一人物を利用してテスト結果の検定をするため、対応のある検定というわけです。
なお対応のあるデータを分析することになるため、二元配置分散分析では以下のような折れ線グラフを描くことができます。
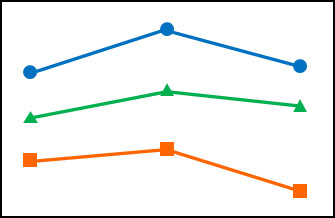
たて軸を列、横軸を行に設定することで、こうしたグラフを描くのです。
二元配置分散分析で差があるときの検定の概念
それでは、どのような理論によってグループ間の差を検定するのでしょうか。一元配置分散分析の場合、群間変動と群内変動を利用することによって差があるかどうかを確認します。差がある場合、それぞれの群の平均が異なるため、これによって群間変動の値が大きくなるのです。
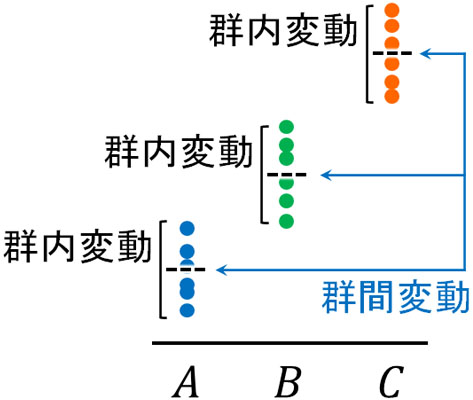
つまり一元配置分散分析というのは、正確には分散の比較ではなく、「群の平均値がどれだけズレているのか」を比較します。ただ同じ群で分散の違いがあるため、群内変動を利用して補正するというわけです。
同じように二元配置分散分析でも、それぞれの群の平均値を比較します。平均値を比較した結果、ばらつき(分散)に違いがある場合、差があると判断します。
このとき、もし行間で差があるとどのような折れ線グラフになるでしょうか。行に着目するとき、群の平均値に違いがある場合、折れ線グラフの高さは異なります。つまり、それぞれの折れ線グラフの線は平行に近づきます。
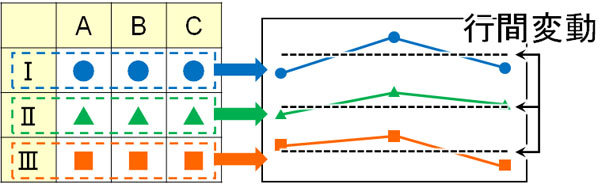
「行間変動に差があることにより、グラフの線の高さに違いが表れる」というのは、行の平均値に違いが表れ、ばらつき(分散)が大きくなることを意味します。
一方で列に着目するとき、差があるケースではグラフはどのような状態になるでしょうか。それぞれの列の平均値が異なる場合、列間に差があるといえます。なお列間に違いがある場合、列ごとの平均値の高さに違いが表れます。
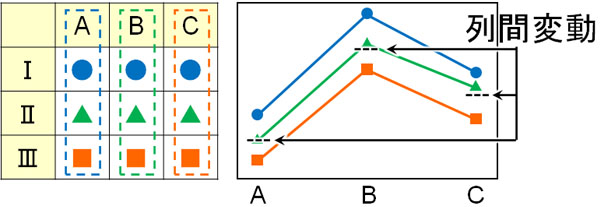
それに対して、行間変動や列間変動がない場合(差がない場合)はどのようなグラフになるのでしょうか。
行間変動がない場合、横軸の折れ線グラフの高さに差が表れません。また列間変動がない場合、列ごとの高さに違いがありません。そのため、以下のようなグラフになります。
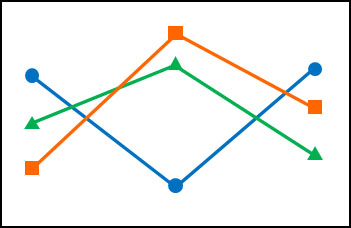
このような場合、行に着目するときの平均値がほぼ同じになります。また列に着目するときについても、平均値がほぼ同じになります。行や列に着目するとき、差がない場合は平均値の違いが少なくなり、F値は1に近づきます。
二元配置分散分析によって何を比較するのかというと、このように行と列についてそれぞれ平均値を比較します。その結果、ばらつき(分散)が大きい場合はF値が大きくなり、差があると判断できるのです。
・どのグループ間で差があるのかは不明
なおすべての分散分析に共通しますが、有意差があるとわかったとしても具体的にどのグループ間で差があるのか判断することはできません。そのため有意水準とp値を比較して有意差が出た場合、次はそれぞれの群について2群検定(t検定)と多重比較法を行うことになります。
2群検定と多重比較法を行うことによって、どのグループ間で差があるのか突き止めることができます。そのため二元配置分散分析によって有意差が出た後、さらなる検定をするのが一般的です。
行間変動・列間変動を利用し、誤差変動を求める
それでは、実際に行間変動と列間変動を計算してみましょう。先ほどの例題を利用する場合、以下のように平均値と分散をそれぞれまとめるといいです。
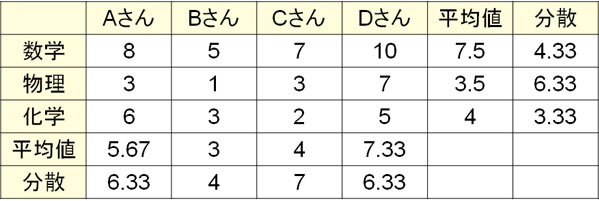
※バートレット検定によって、行と列はそれぞれデータが等分散であると確認できているものとします。
また、二元配置分散分析では総平均を求めなければいけません。すべてのセルの値を足した後、セルの数で割りましょう。そうすると、総平均は5とわかります。
\((8+5+7+10+3\)\(+1+3+7\)\(+6+3+2\)\(+5)/12=5\)
そこで総平均を利用し、行間変動と列間変動を計算しましょう。
・行間変動の偏差平方和SAや自由度dA、分散\((s_A)^2\)を求める
行間変動を求める場合、行ごとの平均値と総平均との差を二乗し、すべて足しましょう。公式は以下になります。
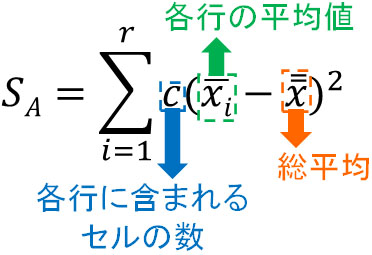
実際に計算すると以下のようになります。
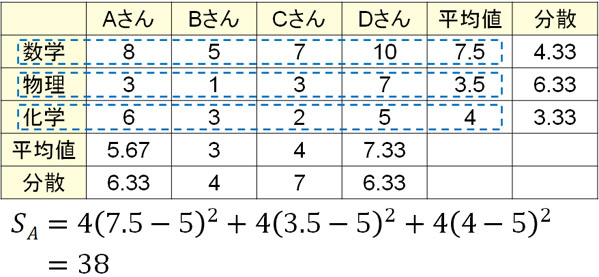
こうして、行間変動(偏差平方和)SAは38であるとわかりました。また、自由度dAは行数から1を引きます。そのため自由度dAは\(3-1=2\)です。
なお、行間変動の分散は偏差平方和SAと自由度dAを利用し、以下の公式で表されます。
\((s_A)^2=\displaystyle\frac{S_A}{d_A}\)
そのため、行間変動の分散は19です。
\((s_A)^2=\displaystyle\frac{38}{2}=19\)
・列間変動の偏差平方和SBや自由度dB、分散\((s_B)^2\)を求める
先ほどと同じように考えて列間変動を計算しましょう。列に着目するため、公式は以下になります。
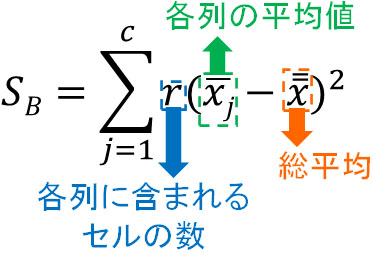
実際の計算は以下のようになります。
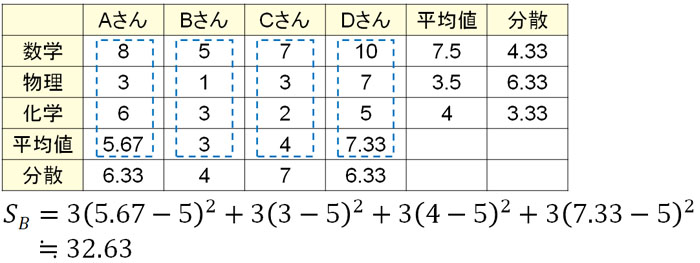
群間変動の偏差平方和SBは32.63です。なお、自由度dBは列の数に1を引きます。そのため、自由度は\(4-1=3\)になります。
列間変動の分散については偏差平方和SBと自由度dBを利用し、以下の公式で表されます。
\((s_B)^2=\displaystyle\frac{S_B}{d_B}\)
そのため、列間変動の分散は10.88です。
\((s_B)^2=\displaystyle\frac{32.63}{3}≒10.88\)
F値を出すために必要な誤差変動(残差)を算出する
次に行うのが誤差変動(残差)の計算です。二元配置分散分析ではF値(分散比)を計算することになります。このとき、誤差変動を利用することでF値を計算するのです。
一元配置分散分析を計算するときについても、群内変動(誤差変動)を利用して分散比を計算したと思います。以下が一元配置分散分析でF値を得るための公式です。

同じように、二元配置分散分析を利用するときについても誤差変動(残差)を利用してF値を得るというわけです。二元配置分散分析では以下の公式によってF値を計算できます。

つまり、一元配置分散分析と同じ方法によってF値(分散比)を計算することができます。誤差というのは、真の値からどれだけズレているのかを表します。そこで誤差に対する補正をします。
それでは、誤差変動はどのようにして求めればいいのでしょうか。誤差変動を求める前に、総変動(合計)の偏差平方和STを計算しましょう。総変動の計算では、すべてのセルの値について総平均を引き、二乗した後に足しましょう。公式で記すと以下のようになります。
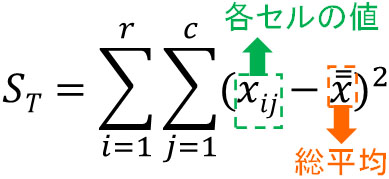
また、実際の計算では以下になります。
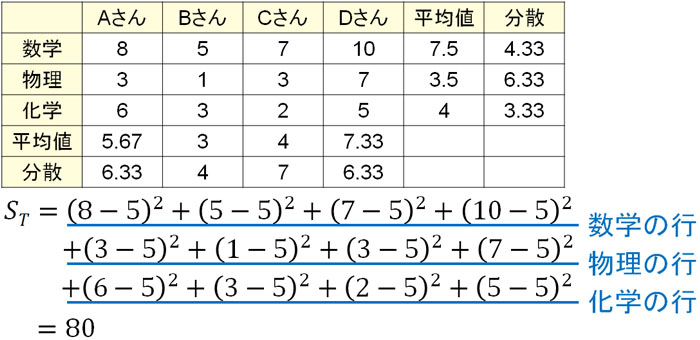
総平均5を利用し、すべてのセルについて計算した値を足すことによって、総変動の偏差平方和STとして80を得ることができました。
総変動の自由度dTについては、行の数と列の数をかけ、1を引いた数になります。行の数は3であり、列の数は4です。そのため、自由度は11です。
\(3×4-1=11\)
・誤差変動の計算を行う
次に、総変動の偏差平方和STを利用して誤差変動(残差)を計算してみましょう。誤差変動SEというのは、総変動(偏差平方和ST)と行間変動(偏差平方和SA)、列間変動(偏差平方和SB)を利用して以下の公式で計算できます。
- \(S_E=S_T-S_A-S_B\)
そのため、誤差変動SEは9.37とわかります。
\(S_E=80-38-32.63=9.37\)
なお誤差変動の自由度dEについては、以下の公式を利用して計算をします。
- \(d_E=d_T-d_A-d_B\)
そのため自由度dEは\(11-2-3=6\)です。このとき誤差変動の分散については誤差変動の偏差平方和SEと自由度dEを利用し、以下の公式で表されます。
\((s_E)^2=\displaystyle\frac{S_E}{d_E}\)
そのため、誤差変動の分散は1.56です。
\((s_E)^2=\displaystyle\frac{9.37}{6}≒1.56\)
なお二元配置分散分析を行えるようになりたい場合、「なぜこのような計算になるのか」を理解するのは意味がありません。私たちは数学者ではないため、数学者が考えてくれた数式を利用させてもらいましょう。
分散分析表を利用し、分散比を計算する
ここまでの計算により、行間変動や列間変動、誤差変動(残差)を得ることができました。そこで表(分散分析表)を作りましょう。以下のようになります。
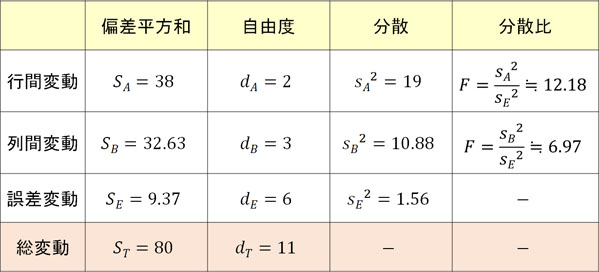
総変動の偏差平方和STと自由度dTを計算した理由としては、誤差変動の偏差平方和SEと自由度dEを得るためです。
また前述の通り、誤差変動の偏差平方和SEと自由度dEがわかれば、誤差変動の分散を求めることができるため、F値(分散比)を計算することができます。行間変動の分散に対して、誤差変動の分散を割ることによって行間変動のF値(分散比)を得られます。同様に計算することによって、列間変動のF値(分散比)を得ることもできます。
F分布に従うため、F値を利用して確率を求める
分散分析表を作ったら、差があるかどうか判断することができます。有意水準が0.05(または0.01)となるF値と比べることによって、有意差を判断するのです。それでは、実際に有意差があるかどうか確認してみましょう。
・行に着目するときの有意差
教科(数学・物理・化学)について、テストの難易度に違いがあるかどうかを知りたい場合、行に着目しましょう。帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:教科によってテストの難易度に差はない
- 対立仮説:教科によってテストの難易度に差がある
行のF値というのは、自由度dAと自由度dEのF分布に従います。自由度dAは2であり、自由度dEは6です。このとき有意水準が0.05となるF値は5.14です。
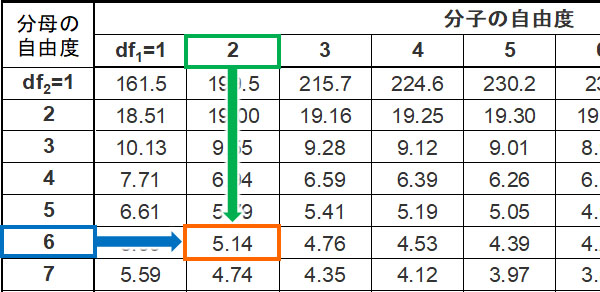
そのたF値が5.14よりも大きい場合、5%以下で起こる稀な現象が発生していると判断できます。
先ほど計算した分散分析表を確認すると、行間変動でのF値(分散比)は12.18です。つまり有意水準0.05(5%)となるF値5.14よりも大きい値であり、帰無仮説を棄却できます。そこで対立仮説を採用し、教科によってテストの難易度に差があると判断できます。
・列に着目するときの有意差
次に、列に着目しましょう。つまり、人によって学力に差があるかどうかに着目するのです。帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:人によって学力に差はない
- 対立仮説:人によって学力に差がある
列に着目する必要があるため、列間変動の値を利用しましょう。列間変動の自由度dBは3です。また誤差変動の自由度dEは6です。有意水準を0.05とすると、自由度dBが3、自由度dEが6のとき、F値は4.76です。
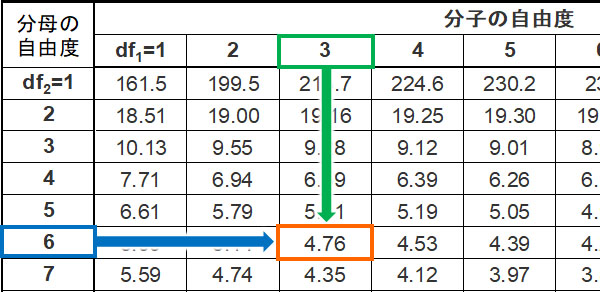
つまりF値が4.76よりも大きい場合、5%以下で発生する稀な現象が発生していると判断できます。
そこで先ほど計算した分散分析表を確認すると、列間変動の分散比(F値)は6.97です。つまり有意水準0.05となるF値4.76よりも大きい値であり、帰無仮説を棄却できます。そこで対立仮説を採用し、人によって学力に差があると判断できます。
なお実際には、前述の通り有意水準とp値を比較して有意差があるとわかった場合、2群検定や多重比較法を利用し、どのグループ間で差があるのか確認することになります。ただいずれにしても、二元配置分散分析を利用することによって差があるかどうか大まかに判断できるようになります。
繰り返しあり(交互作用)の場合の検定方法
ここまで、繰り返しなしの場合の二元配置分散分析について解説してきました。繰り返しのない二元配置分散分析では、2つの因子は互いに独立しています。つまり、2つの因子が影響しあうことはありません。
ただ現実世界はより複雑であり、2つの因子が影響しあうことがあります。例えばワインを単独で飲むよりも、料理と一緒にワインを楽しむとよりおいしく感じます。料理とアルコールは互いに影響しあうため、多くの人が食事と一緒にアルコールを楽しむのです。
またスポーツ飲料の効果を調べるとき、人の状態によって効果は大きく変わります。例えば満腹の人では効果が薄いものの、スポーツ後の人への効果は大きいです。要は、どれだけのどが渇いているのかによって大きく影響を受けます。
こうした影響を交互作用といいます。一元配置分散分析の場合、因子は一つなので交互作用を考慮する必要はありません。ただ二元配置分散分析の場合、交互作用が存在するかもしれないのです。
それでは、交互作用をどのように調べればいいのでしょうか。繰り返しのない二元配置分散分析では、交互作用を調べることができません。そこで交互作用を調べるためには、同じ組み合わせを一回以上繰り返して実験しましょう。
これによって二つの因子による単独効果(主効果)に加えて、二つの因子を組み合わせることによる効果(交互作用)を調べることができます。
交互作用があるケースと交互作用がないケース
それでは、どのように交互作用があると判断すればいいのでしょうか。主効果に加えて交互作用があるケースを調べるためには、前述の通り同じ組み合わせを1回以上は繰り返します。
例えば植物を育てるとき、植物の高さについて、毎日の水の量を変えて計測するとします。水やりの量は変えるものの、水やり作業を繰り返し行うことによって、植物の成長度合いを確認するのです。このとき、例えば以下のようなグラフを得たとします。
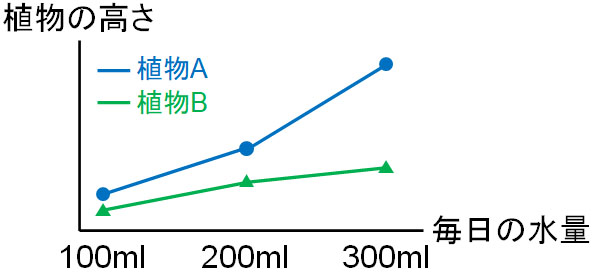
この場合、繰り返しのある二元配置分散分析について、交互作用があると判断します。植物Bに比べて、植物Aでは毎日の水量を多くすることによって成長スピードが大きくなっているからです。水やりでの水量を多くするほど成長する植物の場合、交互作用によってこのような結果を得られます。
ただ、植物Aの成長スピードが速くなるというデータを得られたとしても、それは誤差かもしれません。そこで同じ方法で繰り返し実験すれば、平均値がわかります。これにより、交互作用の有無を判断できるようになります。
また場合によっては、以下のような結果を得られるかもしれません。
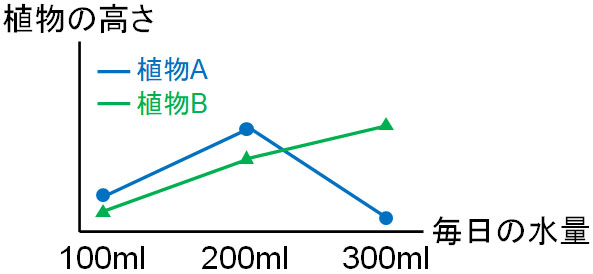
この場合、植物Aでは水量を多くすることによって根が腐ってしまい、結果として枯れてしまったのかもしれません。いずれにしても、水やりの水量を多くすることによってマイナスの効果(交互作用)があったと判断できます。
こうした事例からわかる通り、折れ線グラフを比べたとき、ほかの値に比べて明らかに上昇率が高い(または下落幅が大きい)という場合に交互作用があると判断します。
一方で交互作用がない場合、以下のように折れ線グラフは平行になります。

交互作用がない場合、データには主効果のみ表れます。その他の影響がないため、折れ線グラフは平行になるというわけです。交互作用があるかどうかを調べるとき、折れ線グラフが平行かどうかを確認することで交互作用の有無を把握できます。
二元配置分散分析を利用し、対応のある3群以上を調べる
一元配置分散分析に対して、より複雑になるのが二元配置分散分析です。二元配置分散分析では二つの因子について、行と列でそれぞれ結果を得ることができます。そこで3群以上を調べたいとき、因子が二つの場合は二元配置分散分析を利用しましょう。
二元配置分散分析では行間変動や列間変動など、難しい概念を学ばなければいけません。そこで、これらが何を意味しているのか理解しましょう。
なお繰り返しのない二元配置分散分析だけでなく、繰り返しのある二元配置分散分析を学ばなければいけないことも多いです。この場合、主効果に加えて交互作用があるかどうかを判断できるようになります。
統計学では公式を覚える必要はありません。実際の計算は表計算ソフトがしてくれるからです。ただ表計算ソフトによって得られた結果が何を意味しているのか理解するため、二元配置分散分析の概念を学びましょう。