二次関数を学んだあと、次に勉強することになるのが二次不等式です。二次不等式では不等号が利用され、\(x\)の値によって\(y\)の値がプラスになるのかマイナスになるのか確認します。
実際に二次不等式を解く場合、因数分解をしたり判別式(\(D\))を利用したりします。これによって、\(x\)がどの値のときに二次不等式が成り立つのか判断できるようになります。
ただ二次不等式の問題では、連立方程式や絶対値を利用した問題も出されます。また放物線の位置を決定させる問題も出されます。これらについて、解き方を理解していないと答えを出すのが難しいです。そのため、どのように答えを得ればいいのか学びましょう。
なお二次関数が関わる問題の中でも、二次不等式はグラフを毎回描くのが重要です。そうしないとミスをする確率が高くなるからです。そこで、どのように二次不等式の問題を解けばいいのか解説していきます。
もくじ
\(y\)の値で二次不等式の答えを判断する
一次不等式では、不等号を含む問題が出されます。例えば、\(x+1>0\)の式が該当します。この場合、\(x>-1\)と答えを出すことができます。これは\(y=x+1\)の式について、「\(y\)がプラスの値になる\(x\)の範囲」を求めているのと意味が同じです。\(y=x+1\)であるため、\(x+1>0\)を\(y>0\)に変換できるからです。
二次不等式の問題を解くときについても同じように考えましょう。二次関数に不等号を含む式が二次不等式です。例えば、以下のような式になります。
- \(x^2-x-6>0\)
これはつまり\(y=x^2-x-6\)の二次関数について、\(y>0\)となる\(x\)の範囲を求めればいいことがわかります。
二次関数のおさらいをすると、\(x\)軸との交点を求めるためには、\(y=0\)となる部分がどこになるのかを調べればいいです。また、\(x^2-x-6>0\)を因数分解すると以下のようになります。
- \((x-3)(x+2)>0\)
こうして、\(x\)軸との交点は\(x=-2,3\)であることがわかります。\(y=(x-3)(x+2)\)とすると、\(x=-2,3\)のときに\(y=0\)になるからです。またこのグラフは下に凸なので、以下のようなグラフを描くことができます。
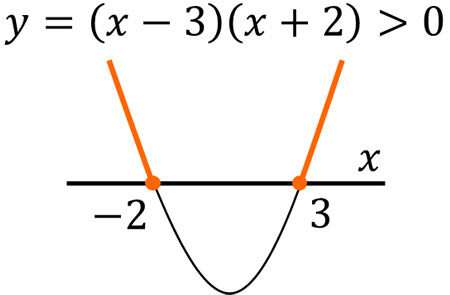
このようにグラフを描くと、\(x^2-x-6>0\)となるためには、\(x<-2,3<x\)となることがわかります。\(x\)の値によって\(y\)の値は変わります。そこで\(y=x^2-x-6>0\)と考え、\(y\)の値がプラスになる部分を探しましょう。そうすれば、\(x\)の範囲を求めることができます。
・グラフを描くことがミスをしないコツ
なお二次不等式の問題を解くとき、必ず簡単なグラフを描くようにしましょう。そうすると、ミスをする可能性が低くなります。
例えば\((x-3)(x+2)>0\)の答えを出すとき、人によっては\(-2<x<3\)と答えてしまうかもしれません。場合によっては、\(x<3,-2<x\)と答えを出してしまうこともあります。これらの答えは間違いであり、正しい答えは\(x<−2,3<x\) です。そこで簡単なグラフを描きましょう。そうすればミスを防げます。
二次不等式では4つのパターンがある
なお二次不等式のグラフには4つのパターンがあります。それぞれ以下のようになります(\(a>0\)である下に凸のグラフで解説しています)。
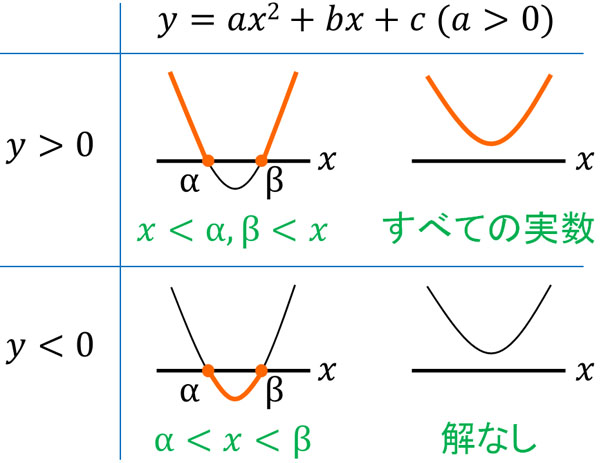
\(y>0\)の場合、\(x\)軸と共有点をもつかどうかによって\(x\)の範囲が異なります。上の図で\(x\)軸と共有点をもつ場合、\(x=α,β\)とするとき、グラフより答えは\(x<α、β<x\)になるとわかります。また\(x\)と共有点をもたない場合、\(x\)がどの数字であっても\(y>0\)になります。そのため、すべての実数が答えです。
一方で\(y<0\)の二次不等式はどのように考えればいいのでしょうか。\(x\)軸と共有点をもつ場合、グラフより\(α<x<β\)のときに\(y<0\)になるとわかります。ただ\(x\)軸と共有点をもたない場合、\(y<0\)になる部分はありません。そのため、解なしとなります。
なお、先ほどの図は前述の通り\(a>0\)のグラフ(下に凸のグラフ)です。二次不等式では\(a<0\)のグラフ(下に凸のグラフ)もあるため、必ずグラフを描くことで問題を解くようにしましょう。
因数分解または解の公式によって二次不等式を作る
なお二次不等式の問題を解くとき、因数分解または判別式を利用します。\(x\)軸との交点を調べることによって、\(x\)の範囲を調べることができます。問題を解く順番は以下になります。
- 因数分解を行う
- 因数分解できない場合、判別式を使う
- \(D>0\)の場合、解の公式を利用する
二次関数でも二次不等式でも、因数分解できる場合は素早く答えを得ることができます。先ほど、\(x^2-x-6>0\)を因数分解することによって、\((x-3)(x+2)>0\)へと変形しました。その結果、\(x<-2,3<x\)という答えを得ました。
・判別式や解の公式を利用する
一方、因数分解できないケースもあります。この場合、どのように二次不等式の問題を解けばいいのでしょうか。まず、\(D\)(判別式)を利用することによって\(x\)軸との交点をもつかどうかを調べましょう。
\(D<0\)では、\(x\)軸との交点はないとわかります。この場合、答えは「すべての実数」または「解なし」です。下に凸、または上に凸のグラフを描くことによって、「すべての実数」「解なし」のどちらが答えなのかを確認しましょう。
なお、\(D≧0\)の場合は\(x\)軸との交点があります。そこで解の公式を利用し、答えを出しましょう。例えば、以下の二次不等式の答えは何でしょうか。
- \(x^2+2x-1<0\)
\(y=x^2+2x-1\)と考えて\(D\)(判別式)を確認すると、以下のようになります。
- \(2^2-4×1×(-1)=8\)
\(D>0\)であるため、\(y=x^2+2x-1\)の二次関数は\(x\)軸と2つの異なる共有点をもちます。そこで、解の公式を利用して答えを出しましょう。以下のようになります。
\(x=\displaystyle\frac{-b±\sqrt{b^2-4ac}}{2a}\)
解の公式に代入すると
\(x=\displaystyle\frac{-2±\sqrt{2^2-4×1×(-1)}}{2×1}\)
\(x=\displaystyle\frac{-2±\sqrt{8}}{2}\)
\(x=\displaystyle\frac{-2±2\sqrt{2}}{2}\)
\(x=-1±\sqrt{2}\)
こうして、\(x=-1±\sqrt{2}\)のときに二次関数のグラフが\(x\)軸と交わるとわかります。なお、必ずグラフを描くことで\(y=x^2+2x-1<0\)の答えを出しましょう。人によっては、グラフを描かないことによって、\(x=-1±\sqrt{2}\)より、\(x<-1±\sqrt{2}\)と答えてしまうことがあります。
そこで、以下のようにグラフを描けば正しい答えを出せるようになります。
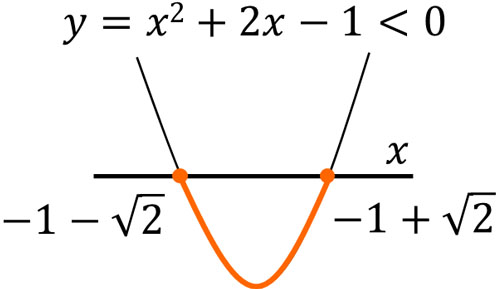
こうして、\(-1-\sqrt{2}<x<-1+\sqrt{2}\)が答えになるとわかります。
二次不等式の解から二次不等式を決定する
なお二次不等式の解から、二次不等式を決定することもできます。例えば、以下の問題の答えは何でしょうか。
- \(ax^2+bx+8>0\)の解が\(-2<x<4\)です。\(a\)と\(b\)の値を求めましょう。
まず、\(y=ax^2+bx+8>0\)の解が\(-2<x<4\)となるためには、どのようなグラフであればいいでしょうか。\(a\)の値がプラスなのかマイナスなのかによってグラフの形が異なります。
そこで簡単なグラフを描くことによって、どちらのグラフが\(y>0\)のときに\(-2<x<4\)となるのか確認しましょう。以下のようになります。
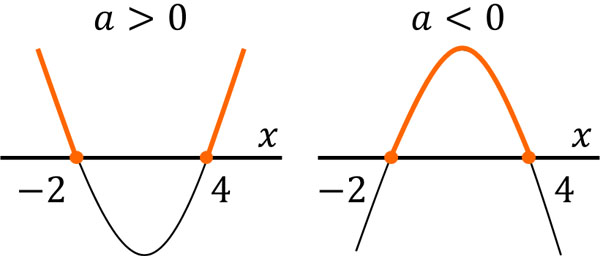
このように\(y>0\)と\(-2<x<4\)の両方を満たすためには、必ず\(a<0\)になるとわかります。グラフを描かないと\(a<0\)になる理由を理解しにくいため、やはり二次不等式の問題を解くときは簡単なグラフを描くのが答えを出すコツになります。
また\(x\)の範囲が\(-2<x<4\)であるため、以下の式を作ることができます。
- \((x-4)(x+2)<0\)
そこで、式の展開をしましょう。以下のようになります。
\((x-4)(x+2)<0\)
\(x^2-2x-8<0\)
ただ前述の通り、必ず\(a<0\)になります。そこで、両辺に-1をかけましょう。すると、以下のようになります。
\(-x^2+2x+8>0\)
その後、\(ax^2+bx+8>0\)と\(-x^2+2x+8>0\)を比較しましょう。その結果、\(a=-1,b=2\)であるとわかります。
実数解をもつ値を決定する
なお場合によっては、二次関数の値が決まっていないことがあります。その場合、判別式を利用することによって実数解をもつ\(x\)の範囲を決めるようにしましょう。
例えば、以下の二次関数が実数解をもたない\(k\)の範囲を求めましょう。
- \(x^2+kx+k+3=0\)
実数解をもつかどうかを判断する方法として、判別式を利用すればいいです。\(D>0\)のとき、二次関数は2つの異なる解をもちます。\(D=0\)のとき、二次関数は1つの解をもちます。\(D<0\)のとき、二次関数は解がありません。
そこで\(D<0\)の式を作りましょう。以下のようになります。
\(D=b^2-4ac<0\)
代入すると
\(k^2-4×1×(k+3)<0\)
\(k^2-4k-12<0\)
\((k+2)(k-6)<0\)
\(y=(k+2)(k-6)<0\)となるためには、\(-2<k<6\)となる必要があります。つまり\(-2<k<6\)のとき、\(x^2+kx+k+3=0\)は解をもちません。こうして、\(k\)の範囲を求めることができます。
連立二次不等式の解き方
ここまでの内容を理解すれば、連立二次不等式の問題を解くことができます。連立二次不等式では、二つの二次不等式を満たす\(x\)の範囲を考えるようにしましょう。
例えば、以下の問題はどのような答えになるでしょうか。
\(\begin{eqnarray} \left\{\begin{array}{l}x^2+3x-4<0\\x^2+5x+6≧0\end{array}\right.\end{eqnarray}\)
まず、それぞれの二次不等式を解きましょう。以下のようになります。
・\(x^2+3x-4<0\)の\(x\)の範囲
\(x^2+3x-4<0\)
\((x-1)(x+4)<0\)
そのため、\(-4<x<1\)となります。
・\(x^2+5x+6≧0\)の\(x\)の範囲
\(x^2+5x+6≧0\)
\((x+2)(x+3)≧0\)
そのため、\(x≦-3,-2≦x\)となります。
※グラフを描いていないものの、実際に\(x\)の範囲を見つけるときは簡単なグラフを描くようにしましょう。そうすれば、計算ミスを減らすことができます。
次に、2つの二次不等式について、\(x\)の範囲がわかったら図にしましょう。以下のようになります。

前述の通り、連立方程式では2つの方程式を満たす必要があります。そこで2つの二次不等式について、両方の条件を満たす\(x\)の範囲を探しましょう。そうすると、\(-4<x≦-3,-2≦x<1\)が答えになるとわかります。
絶対値をもつ二次関数を描く
一方で絶対値をもつ二次関数もあります。これまで、絶対値をもつ一次関数を解いたことがあると思います。同じように、二次関数や二次不等式についても、絶対値をもつ式を解けるようになりましょう。
絶対値の記号を外すときは場合分けをします。値がマイナスになる場合、絶対値の記号を外すときに-1をかけます。つまり、値がプラスなのかマイナスなのかによって場合分けをします。二次関数や二次不等式についても、場合分けをして問題を解くと考えましょう。
例えば、以下の二次関数はどのようなグラフを描くでしょうか。
- \(y=|x^2-5x+6|\)
二次不等式では、前述の通り因数分解できるかどうかを最初に考えましょう。そうすると、以下のように因数分解できます。
- \(y=|(x-2)(x-3)|\)
そこで\(|(x-2)(x-3)|\)の値がプラスになるのか、マイナスになるのかによって場合分けをしましょう。
・\(x≦2,3≦x\)の場合
\(x≦2,3≦x\)の場合、値がプラスになります。そこで、何もせずに絶対値の記号を外しましょう。そうすると、以下の二次関数を得られます。
\(y=(x-2)(x-3)\)
\(y=x^2-5x+6\)
・\(2<x<3\)の場合
\(2<x<3\)の場合、必ず値がマイナスになります。そこで絶対値の記号を外すとき、-1をかけましょう。そうすると、以下の二次関数を得られます。
\(y=-(x-2)(x-3)\)
\(y=-x^2+5x-6\)
これをグラフにすると以下のようになります。

絶対値がある場合、二次関数でも二次不等式でも、必ず場合分けをすることによって答えを出せるようにしましょう。
\(x\)軸の正の部分と負の部分で交わる放物線
ここまでの内容を理解すれば、より発展的な二次不等式の問題を解けるようになります。二次不等式を学べば、どのようなケースで解をもつ二次関数になるのか判断できるようになるのです。
ただ解き方を理解していない場合、答えを出すのが難しいです。そこで、どのようにすれば\(x\)の範囲を求めることができるのかを理解しましょう。例えば以下の式について、二次関数が\(x\)軸の正の部分と負の部分で交わる\(a\)の範囲は何でしょうか。
- \(y=x^2+ax+a\)
どのようなとき、\(x\)軸の正の部分と負の部分で交わるのでしょうか。\(y=x^2+ax+a\)は下に凸のグラフです。このとき、\(f(0)<0\)になればいいことがわかります(\(f(0)\)とは、\(x\)に0を代入するときの\(y\)の値)。
以下のグラフのように、\(x=0\)のときに\(y\)の値がマイナスになる場合、二次関数のグラフは必ず\(x\)軸の正の部分と負の部分に交点をもちます。
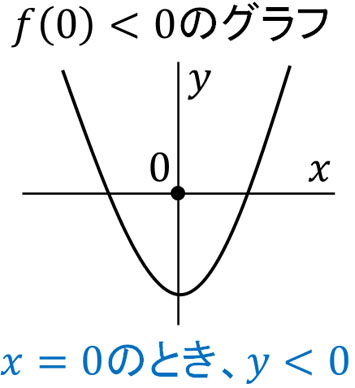
下に凸のグラフの場合、\(x\)の値が増える(または減る)ことによって、\(y\)の値は増えていきます。そのため\(x\)軸の正の部分と負の部分で交わる\(a\)の値を出したい場合、\(f(0)<0\)としましょう。そこで\(y=x^2+ax+a\)について、\(f(0)<0\)となる式を作ります。\(x=0\)を代入すると、以下のようになります。
\(x^2+ax+a<0\):(\(x=0\))
\(a<0\)
こうして\(a<0\)の場合、\(x\)軸の正の部分と負の部分で交わる二次関数になります。
\(y\)の位置、軸、判別式を利用して二次関数の位置を決める
なお、先ほどの解き方は「二次関数が\(x\)軸の正の部分と負の部分で交わる場合」に利用できます。ほかの条件では、どのように答えを出せばいいのでしょうか。
そこで以下の二次関数について、\(x\)軸との2つの交点が正となる場合の\(a\)の範囲を求めてみましょう。
- \(y=x^2-ax+a^2-2a\)
・\(y\)の位置に着目する
\(x\)軸との交点が正になるためには、\(f(0)>0\)でなければいけません。\(x=0\)を代入するとき、\(y\)の値がプラスになっているからこそ、\(x\)軸との交点が正になります。そのため、以下のようになります。
\(f(0)=x^2-ax+a^2-2a>0\):(\(x=0\)を代入)
\(a^2-2a>0\)
\(a(a-2)>0\)
こうして\(a<0,2<a\)の場合、\(f(0)>0\)になるとわかります。つまり\(a<0,2<a\)であれば、\(x=0\)のときに\(y\)の値はプラスになります。
・軸に着目する
ただ\(f(0)>0\)であったとしても、以下のように「\(x\)軸との交点が両方とも正になる」「\(x\)軸との交点が両方とも負になる」の2パターンがあります。
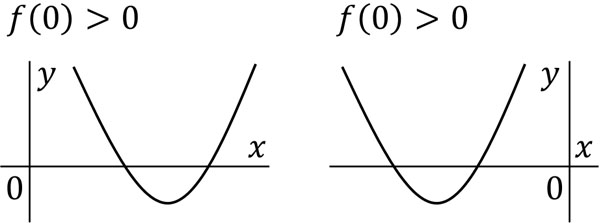
そこで、軸(頂点の\(x\)座標)に着目しましょう。軸が正の位置にあれば、\(x\)軸との交点が両方とも正になります。そこで、軸の位置を調べるために平方完成しましょう。以下のようになります。
\(y=x^2-ax+a^2-2a\)
\(y=(x^2-ax)+a^2-2a\)
\(y=(\color{red}{x^2-ax+\displaystyle\frac{1}{4}a^2}-\displaystyle\frac{1}{4}a^2)+a^2-2a\)
\(y=(x^2-ax+\displaystyle\frac{1}{4}a^2)+\displaystyle\frac{3}{4}a^2-2a\)
\(y=(x-\displaystyle\frac{1}{2}a)^2+\displaystyle\frac{3}{4}a^2-2a\)
こうして、頂点の座標は\((\displaystyle\frac{1}{2}a,\displaystyle\frac{3}{4}a^2-2a)\)になるとわかります。頂点の\(x\)座標が正であればいいため、\(\displaystyle\frac{1}{2}a>0\)である必要があります。そのため、\(a>0\)です。
・判別式に着目する
ただ\(f(0)>0\)であり、頂点の\(x\)座標が正であったとしても、答えを得られないケースがあります。以下のように、\(x\)軸との交点をもたないケースが考えられます。
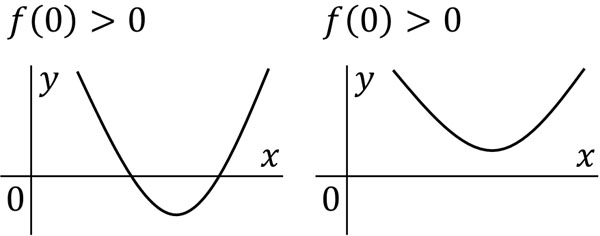
これを防ぐため判別式を利用しましょう。\(D>0\)の場合、二次関数は\(x\)軸との交点をもちます。そのため\(y=x^2-ax+a^2-2a\)について、判別式を利用して以下の式を作ることができます。
\(D=b^2-4ac>0\)
代入すると
\((-a)^2-4×1×(a^2-2a)>0\)
\(a^2-4a^2+8a>0\)
\(-3a^2+8a>0\)
\(a^2-\displaystyle\frac{8}{3}a<0\)
\(a(a-\displaystyle\frac{8}{3})<0\)
こうして、\(0<a<\displaystyle\frac{8}{3}\)になるとわかります。
それでは、先ほど計算した2つの条件を記しましょう。以下のようになります。
- \(f(0)>0\):\(a<0,2<a\)
- 頂点の軸の位置:\(a>0\)
- \(D>0\):\(0<a<\displaystyle\frac{8}{3}\)
\(x\)軸との2つの交点が正となる場合、この3つの条件をすべて満たす必要があります。そのため、答えは\(2<a<\displaystyle\frac{8}{3}\)となります。
二次不等式の問題の解き方を覚える
二次関数の発展問題が二次不等式です。また二次不等式には解き方があるため、どのように答えを出せばいいのか理解するようにしましょう。
二次不等式には4パターンあります。そこでグラフを描き、\(x\)の値によって\(y\)の値がプラスになるのか、それともマイナスになるのか確認しましょう。そうすれば、\(x\)の範囲がわかるようになります。
また放物線と\(x\)軸との交点を求める問題では、解き方を理解していないと答えを出すのが難しいです。そこで\(y\)の位置や軸の位置、判別式を利用することによって、どのような条件のときに式が成り立つのか答えるようにしましょう。
解き方を知っていれば、二次不等式の問題を解けます。一方、解き方を知らなければ答えを出せません。そこで判別式を利用したり座標の位置を確認したりして答えを出しましょう。