三角関数の合成をすることにより、sinθとcosθの足し算をsinθのみの式(またはcosθのみの式)へ変換することができます。三角関数の合成公式を利用することにより、三角関数の計算をすることができます。
sinθとcosθの足し算をするとき、三角関数の和と積の公式を利用できます。ただ、三角関数の合成公式による式の変形もできるのです。なお三角関数の合成公式を覚えるのではなく、作れるようになりましょう。
なお三角関数の合成公式を利用するとき、三角方程式の最大値と最小値を計算するときにも便利です。sinθまたはcosθへまとめることにより、最大値と最小値の計算が可能になります。
それでは、三角関数の合成公式を覚えずに作れるようになるにはどうすればいいのでしょうか。また、どのように公式を用いて三角方程式の計算をすればいいのでしょうか。三角関数の合成公式を利用する方法を解説していきます。
もくじ
三角関数の合成公式と計算方法
三角関数では複数の公式を学ぶことになります。その一つが三角関数の合成公式です。以下が公式になります。
- \(a·sinθ+b·cosθ=\sqrt{a^2+b^2}\)\(sin(θ+α)\)
※\(sinα=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\)、\(cosα=\displaystyle\frac{a}{\sqrt{a^2+b^2}}\)
これが三角関数の合成公式です。
三角関数の合成公式の証明
ただ、公式を見ても意味を理解することができません。そこで公式の証明をすることにより、先ほどの公式が何を表しているのか学びましょう。まず、以下の図を考えます。
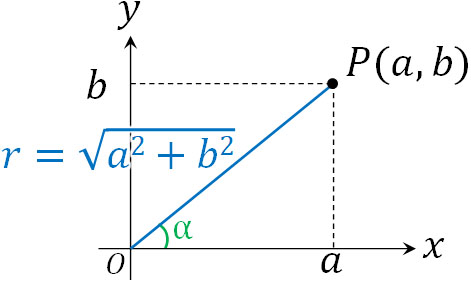
※図より、\(sinα=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\)、\(cosα=\displaystyle\frac{a}{\sqrt{a^2+b^2}}\)であるとわかります。
点Pの座標を\((a,b)\)、OPの長さを\(r\)とすると、\(r=\sqrt{a^2+b^2}\)です。また図より、\(a=r·cosα\)であり、\(b=r·sinα\)です。そのため、計算の途中で加法定理を利用することにより、以下のように式を変形できます。
\(a·sinθ+b·cosθ\)
\(=r·cosαsinθ+r·sinαcosθ\)
\(=r(sinθcosα+cosθsinα)\)
\(=\sqrt{a^2+b^2}(sinθcosα+cosθsinα)\)
\(=\sqrt{a^2+b^2}sin(θ+α)\)
図形を利用することにより、公式を証明することができました。
加法定理の逆を利用し、公式を覚えずに合成する
なお三角関数を学ぶとき、多くの公式を覚えなければいけないように考えてしまいます。ただ実際には公式を作れるため、覚える必要はありません。事実、加法定理を利用することにより、2倍角の公式や半角の公式、3倍角の公式、三角関数の和と積の公式を作ることができます。
三角関数の合成についても、加法定理を用いて作れます。そのため公式を覚えるのではなく、加法定理を用いて計算できるようになりましょう。またこの方法のほうが、図を用いて計算するよりも計算ミスが少ないです。
方法としては、先ほどと同様に加法定理の逆を利用して公式を導出します。ただ、計算過程が少し異なります。以下のように計算しましょう。
\(a·sinθ+b·cosθ\)
\(=\sqrt{a^2+b^2}\)\(\left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}sinθ+\displaystyle\frac{b}{\sqrt{a^2+b^2}}cosθ\right)\)
\(=\sqrt{a^2+b^2}(sinθcosα+cosθsinα)\)
\(=\sqrt{a^2+b^2}sin(θ+α)\)
計算の最初に\(\sqrt{a^2+b^2}\)を利用して、全体を括っています。また\(sinα=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\)、\(cosα=\displaystyle\frac{a}{\sqrt{a^2+b^2}}\)に加え、加法定理の逆を利用することで公式を導出しました。
最初の証明方法と違うのは、\(\sqrt{a^2+b^2}\)を利用して強引に括る部分です。これを活用することにより、公式を利用せずに計算できます。
それでは、実際に公式を利用して計算してみましょう。以下の式について、三角関数の合成をすることによって変形してみましょう。ただし\(r>0\)であり、\(-π<α<π\)とします。
- \(\sqrt{3}sinθ+cosθ\)
\(r\)を計算すると以下のようになります。
\(r=\sqrt{(\sqrt{3})^2+1^2}\)
\(r=2\)
そこで、2を利用して全体を括りましょう。
\(\sqrt{3}sinθ+cosθ\)
\(=2\left(\displaystyle\frac{\sqrt{3}}{2}sinθ+\displaystyle\frac{1}{2}cosθ\right)\)
\(=2\left(sinθcos\displaystyle\frac{π}{6}+cosθsin\displaystyle\frac{π}{6}\right)\)
\(=2sin\left(θ+\displaystyle\frac{π}{6}\right)\)
こうして、三角関数の合成をすることができました。\(cos\displaystyle\frac{π}{6}=\displaystyle\frac{\sqrt{3}}{2}\)であり、\(sin\displaystyle\frac{π}{6}=\displaystyle\frac{1}{2}\)であるため、このように式を変形しましょう。
加法定理の逆を利用して三角関数の合成をする場合、すべての問題で公式を覚える必要がありません。そのため、この方法を利用して三角関数の合成をすることをおすすめします。
cosθを利用して三角関数の合成をする
sinθとcosθは互いに変形できることを既に理解していると思います。そこでsinθだけでなく、cosθへの合成も行えるようになりましょう。
方法は簡単であり、sinθの位相をずらします。具体的には、\(sin\left(θ+\displaystyle\frac{π}{2}\right)=cosθ\)を利用します。
例として、先ほどと同じ条件で\(\sqrt{3}sinθ+cosθ\)をcosθに合成してみましょう。前述の通り、計算すると\(2sin\left(θ+\displaystyle\frac{π}{6}\right)\)になります。そこで、\(sin\left(θ+\displaystyle\frac{π}{2}\right)=cosθ\)を用いてcosθに変形しましょう。
\(2sin\left(θ+\displaystyle\frac{π}{6}\right)\)
\(=2sin\left(θ+\displaystyle\frac{π}{2}-\displaystyle\frac{π}{3}\right)\)
\(=2cos\left(θ-\displaystyle\frac{π}{3}\right)\)
図を利用したり、加法定理の逆を利用したりして、cosθの合成公式を説明する人は多いです。ただ両方とも理解しにくく、計算ミスが起こりやすいです。そこで三角関数の合法方法としてsinθのみ覚え、cosθの合成はsinθから変形しましょう。
最大値と最小値を合成によって計算する
三角関数の合成公式は最大値と最小値を計算するときに便利です。そこで、公式を利用することによって最大値と最小値を得ましょう。\(0≦θ≦π\)のとき、以下の式で最大値・最小値とそのときのθの値を求めましょう。
- \(y=3sinθ-\sqrt{3}cosθ\)
以下のように計算します。
\(y=3sinθ-\sqrt{3}cosθ\)
\(y=2\sqrt{3}\left(sinθ\displaystyle\frac{3}{2\sqrt{3}}-cosθ\displaystyle\frac{1}{2}\right)\)
\(y=2\sqrt{3}\left(sinθ\displaystyle\frac{\sqrt{3}}{2}-cosθ\displaystyle\frac{1}{2}\right)\)
\(y=2\sqrt{3}\left(sinθcos\displaystyle\frac{π}{6}-cosθsin\displaystyle\frac{π}{6}\right)\)
\(y=2\sqrt{3}sin\left(θ-\displaystyle\frac{π}{6}\right)\)
\(0≦θ≦π\)であるため、\(-\displaystyle\frac{π}{6}≦θ-\displaystyle\frac{π}{6}≦\displaystyle\frac{5π}{6}\)です。
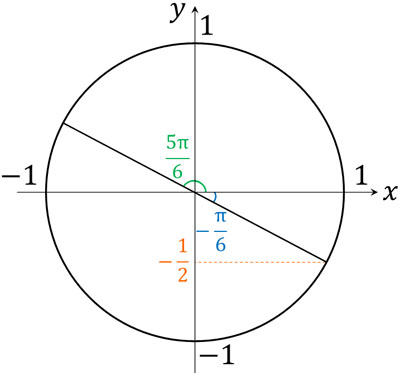
図より、\(sin\left(θ-\displaystyle\frac{π}{6}\right)\)の範囲は以下のようになります。
- \(-\displaystyle\frac{1}{2}≦sin\left(θ-\displaystyle\frac{π}{6}\right)≦1\)
そのため、以下のようになります。
- \(-\sqrt{3}≦2\sqrt{3}sin\left(θ-\displaystyle\frac{π}{6}\right)≦2\sqrt{3}\)
こうして、最大値と最小値がわかりました。なお\(θ-\displaystyle\frac{π}{6}=\displaystyle\frac{π}{2}\)、つまり\(θ=\displaystyle\frac{2π}{3}\)のとき、最大値\(2\sqrt{3}\)です。また\(θ-\displaystyle\frac{π}{6}=-\displaystyle\frac{π}{6}\)、つまり\(θ=0\)のとき、最小値\(-\sqrt{3}\)です。
sinθとcosθの対称式の解き方
2つの変数を交換しても式が変化しない場合、対称式といいます。sinθとcosθによる対称式では、問題の解き方があります。具体的には、\(sinθ+cosθ=t\)と設定しましょう。\(t\)を二乗すると以下のようになります。
\(t^2=sin^2θ+2sinθcosθ\)\(+cos^2θ\)
\(t^2=1+2sinθcosθ\)
\(2sinθcosθ=t^2-1\)
\(sinθcosθ=\displaystyle\frac{t^2-1}{2}\)
そこで、\(sinθcosθ=\displaystyle\frac{t^2-1}{2}\)を利用して答えを得るのです。それでは、以下の問題の答えは何でしょうか。
- \(y=sin2θ-2sinθ-2cosθ+1\)の最大値と最小値を求めましょう。なお、\(0≦θ≦π\)です。
2倍角の公式より、\(sin2θ=2sinθcosθ\)です。そのため、式を以下のように変形できます。
- \(y=2sinθcosθ-2sinθ-2cosθ+1\)
そこで\(sinθ+cosθ=t\)と置くと、以下のように式を変形できます。
\(y=2sinθcosθ-2sinθ-2cosθ+1\)
\(y=2sinθcosθ-2(sinθ+cosθ)+1\)
\(y=2×\displaystyle\frac{t^2-1}{2}-2t+1\)
\(y=t^2-2t\)
\(y=(t-1)^2-1\)
こうして、軸が\(t=1\)となる下に凸の二次関数であるとわかります。
・\(t\)の範囲を計算する
次に\(t\)の範囲を計算しましょう。三角関数の合成をすることにより、sinθの式にするのです。以下のように計算しましょう。
\(t=sinθ+cosθ\)
\(t=\sqrt{2}\left(sinθ\displaystyle\frac{1}{\sqrt{2}}+cosθ\displaystyle\frac{1}{\sqrt{2}}\right)\)
\(t=\sqrt{2}sin\left(θ+\displaystyle\frac{π}{4}\right)\)
こうして、sinθを利用して\(t\)を表すことができました。なお\(0≦θ≦π\)であるため、\(\displaystyle\frac{π}{4}≦θ+\displaystyle\frac{π}{4}≦\displaystyle\frac{5π}{4}\)です。そのため、\(-\displaystyle\frac{1}{\sqrt{2}}≦sin\left(θ+\displaystyle\frac{π}{4}\right)≦1\)です。
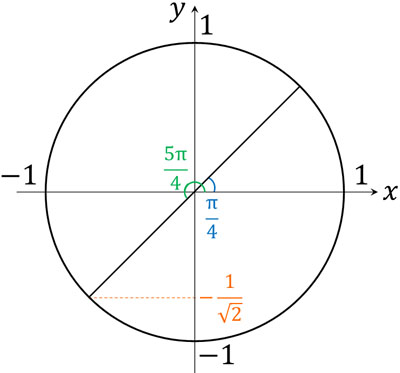
ここまでの計算により、\(t\)の範囲がわかります。
\(-\displaystyle\frac{1}{\sqrt{2}}≦sin\left(θ+\displaystyle\frac{π}{4}\right)≦1\)
\(-1≦\sqrt{2}sin\left(θ+\displaystyle\frac{π}{4}\right)≦\sqrt{2}\)
\(-1≦t≦\sqrt{2}\)
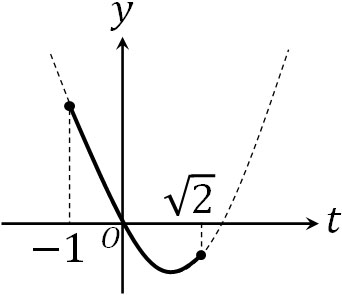
\(t=-1\)のとき、最大値は3です。θは以下のように計算しましょう。
\(\sqrt{2}sin\left(θ+\displaystyle\frac{π}{4}\right)=-1\)
\(sin\left(θ+\displaystyle\frac{π}{4}\right)=-\displaystyle\frac{1}{\sqrt{2}}\)
\(θ+\displaystyle\frac{π}{4}=\displaystyle\frac{5π}{4}\)
\(θ=π\)
そのため\(θ=π\)のとき、最大値3となります。また\(t=1\)のとき、最小値は-1です。θは以下のように計算しましょう。
\(\sqrt{2}sin\left(θ+\displaystyle\frac{π}{4}\right)=1\)
\(sin\left(θ+\displaystyle\frac{π}{4}\right)=\displaystyle\frac{1}{\sqrt{2}}\)
\(θ+\displaystyle\frac{π}{4}=\displaystyle\frac{π}{4},\displaystyle\frac{3π}{4}\)
\(θ=0,\displaystyle\frac{π}{2}\)
こうして\(θ=0,\displaystyle\frac{π}{2}\)のとき、最小値-1になるとわかりました。三角関数では置き換えによって計算できるようになることは多く、その代表的な例の一つが対称式です。
公式なしに三角関数の合成を行う
三角関数を学ぶとき、できるだけ公式を覚えないようにする必要があります。三角関数に関わる公式は多く、すべての公式を覚えるのは現実的ではありません。そこでsinθとcosθに関わる加法定理のみを覚え、ほかの公式は作れるようになりましょう。これは、三角関数の合成公式についても同様です。
加法定理の逆を利用することにより、三角関数の合成を行うことができます。この方法のほうが計算ミスは少ないです。また\(sin\left(θ+\displaystyle\frac{π}{2}\right)=cosθ\)を利用することにより、sinθをcosθへ変換することもできます。
そこで三角関数の合成を行うことにより、三角方程式を解けるようになりましょう。特に最大値と最小値の計算をするとき、三角関数の合成は有効です。
公式を覚えてはいけない内容の一つが三角関数の合成です。方法を学べば、簡単な計算によって三角関数の合成を行えるようになります。






