磁場が存在する場合、電流が流れることによって電流は磁場から力を受けます。このとき、自由電子が動くことによって電流が発生します。そのため、電子に対して磁場による力が加わっているといえます。
こうした力がローレンツ力です。非常に小さいミクロの世界に着目し、力の大きさを計算するのです。
なお、ローレンツ力を計算するときは円運動を利用することになります。そのため、力学で学んだ円運動を復習しましょう。
それでは、どのようにしてローレンツ力の計算をすればいいのでしょうか。また、なぜ磁場の影響を電子が受けるときは円運動になるのでしょうか。ローレンツ力の概念や公式、円運動を利用しての計算方法を解説していきます。
もくじ
荷電粒子が磁場から受ける力がローレンツ力
自由電子が動くことで電流が発生します。そのため電流が磁場から力を受けるというのは、言い換えると「自由電子が磁場から力を受けている」と判断できます。
また、荷電粒子(自由電子)が磁場から受ける力をローレンツ力といいます。ローレンツ力によって電子が磁場から力を受け、結果として電流が力を受けるようになるのです。
電流が受ける力\(F\)を計算するとき、磁束密度\(B\)、電流の大きさ\(I\)、磁場の影響を受ける物体の長さ\(l\)を利用して以下のように計算します。
- \(F=BIl\)
一方、ローレンツ力では自由電子に着目して力の大きさを計算します。
ローレンツ力を得る公式
自由電子は電気量をもちます。当然、荷電粒子の電気量\(q\)が大きいほど磁場から受ける力は大きくなります。また荷電粒子のスピード\(v\)が速いと、その分だけ電流は大きくなります。1秒間に流れる電気量が電流の定義だからです。
つまり、荷電粒子の電気量\(q\)が大きいほど、導線を移動するスピード\(v\)が速いほど、磁場から受ける力が大きくなります。
また、磁場の性質を表す値が磁束密度\(B\)です。そこで、以下の公式によってローレンツ力\(f\)を計算しましょう。
- \(f=qvB\)
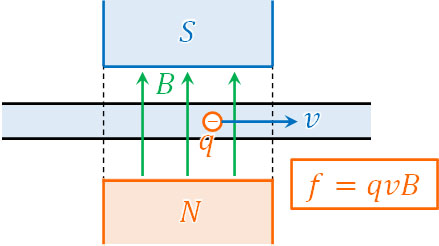
電気量\(q\)とスピード\(v\)の値が大きい場合、それに比例してローレンツ力が大きくなるのは容易に想像できると思います。それに加えて磁束密度\(B\)をかけることで、ローレンツ力を得るというわけです。
なお、角度がある場合はsinθまたはcosθを利用することで計算しましょう。電流が磁場から力を受けるとき、磁場に対して電流の向きが直角となるように補正する必要があります。同様に、ローレンツ力を得るときについても、速さに対して角度を利用することで補正しましょう。
例えば、以下の図を考えてみましょう。
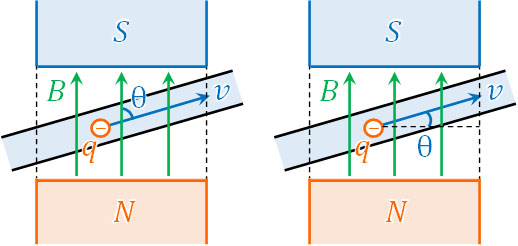
左図では、\(vsinθ\)によって磁場と直角となる速さを得ることができます。そのため、以下の式によってローレンツ力を計算できます。
- \(f=qvBsinθ\)
また右図では、\(vcosθ\)によって、磁場に対して速さが直角になります。そのため、ローレンツ力を計算する式は以下になります。
- \(f=qvBcosθ\)
このように角度を利用することによってローレンツ力を得ましょう。
フレミングの左手の法則を利用し、ローレンツ力の向きを把握する
それでは、ローレンツ力の向きはどのように確認すればいいのでしょうか。電流が磁場から力を受けるとき、力の大きさを計算するだけでなく、力の向きを把握しなければいけません。これはローレンツ力も同様です。
一つの電子が受ける力(ローレンツ力)をすべて足すと、電流が受ける力を計算できます。そのため磁場によって電流が受ける力\(F\)とローレンツ力\(f\)の向きは当然ながら同じです。つまり、フレミングの左手の法則を利用すれば、ローレンツ力の向きがわかります。
・電流の向きと荷電粒子が動く向きに注意が必要
なお、荷電粒子が動く向きと電流の向きは異なるケースがあることを理解しましょう。プラスに荷電している粒子が動くと考える場合、電流の向きと荷電粒子の向きは同じです。しかし、マイナスに荷電している粒子が動くと仮定する場合、電流の向きと荷電粒子の向きは逆です。
例えば、電流の向きと自由電子は向きが逆であることを既に知っていると思います。
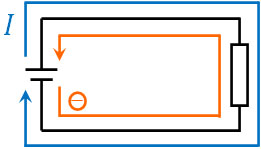
フレミングの左手の法則を利用する場合、中指を電流の向きに合わせる必要があります。そのため荷電粒子の電荷がマイナスの場合、粒子(電子)が進む向きとは反対方向に電流が流れていると考え、フレミングの左手の法則を利用しましょう。

荷電粒子の電荷がプラスの場合、電流の向きと粒子が進む向きは同じです。一方で、電子のように電荷がマイナスの場合、電流の向きと粒子が進む向きは反対です。
磁場中の荷電粒子は等速円運動をする
フレミングの左手の法則では、磁場(磁束密度)の向き、粒子が進む向き、力を受ける向きが必ず垂直になります。もし磁場と粒子の進む向きが同じ場合、力を受けることはありません。
それでは以下のように、プラスの電荷をもつ粒子が速さ\(v\)で上方向(天井)に進んでいる状態を考えましょう。磁場(磁束密度)の向きは、この画面の裏からあなたの顔に向かっているとします。この場合、ローレンツ力の向きは右です。
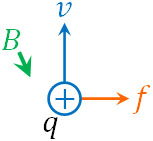
進んでいる方向に対して、垂直に力を受ける場合、どのような運動をするのでしょうか。力学では、「同じ速さで動いている物体に対して、力(加速度)が垂直に加わる場合、等速円運動をする」と学びます。
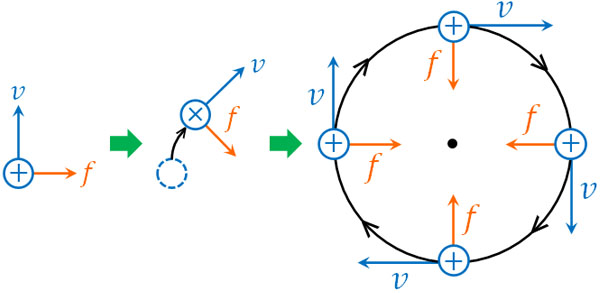
実際に、あなたの左手を利用して等速円運動になることを確認しましょう。磁場はこの画面の裏側からあなたの顔に向かっており、速さの向きは時間経過と共に変化します。この場合、力の向きは必ず円の中心になります。
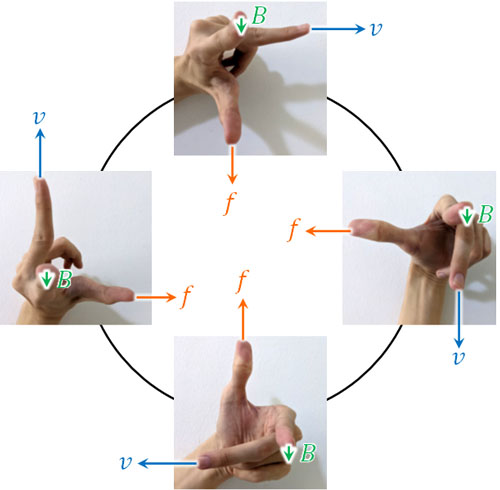
このように確認すると、荷電粒子は等速円運動をしているとわかります。なお、以下では等速円運動を理解しているという前提で話を進めていきます。そのため等速円運動の内容を忘れてしまっている場合、必ず復習しましょう。
運動方程式を利用し、周期と角速度を得る
それでは、運動方程式を利用することで式を作りましょう。荷電粒子の重さを\(m\)、中心方向への加速度を\(a\)とすると、ローレンツ力\(f\)との関係は以下のようになります。
- \(f=ma\)
なお前述の通り、\(f=qvB\)です。そのため、以下の関係が成り立ちます。
- \(ma=qvB\)
次に、等速円運動を利用して運動方程式を立てましょう。等速円運動では、加速度\(a\)は速さ\(v\)と円の半径\(r\)を利用して、\(a=\displaystyle\frac{v^2}{r}\)と表すことができます。そのため、以下のように式を変形できます。
- \(m\displaystyle\frac{v^2}{r}=qvB\)
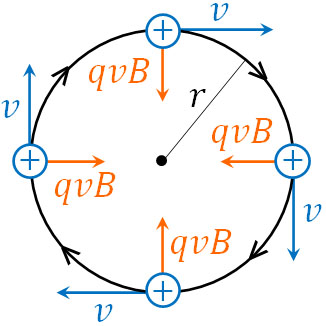
\(m\displaystyle\frac{v^2}{r}=qvB\)であるため、\(v=\displaystyle\frac{qBr}{m}\)です。
また角速度\(ω\)と周期\(T\)をかけると\(2π\)になります。そのため、\(ωT=2π\)です。等速円運動の公式より、\(v=rω\)であるため、\(ω=\displaystyle\frac{v}{r}\)です。そこで\(ω=\displaystyle\frac{v}{r}\)を\(ωT=2π\)に代入すると、以下のようになります。
\(ωT=2π\)
\(\displaystyle\frac{v}{r}T=2π\)
\(v=\displaystyle\frac{2πr}{T}\)
次に、\(v=\displaystyle\frac{2πr}{T}\)を\(v=\displaystyle\frac{qBr}{m}\)へ代入しましょう。
\(v=\displaystyle\frac{qBr}{m}\)
\(\displaystyle\frac{2πr}{T}=\displaystyle\frac{qBr}{m}\)
\(T=\displaystyle\frac{2πm}{qB}\)
こうして、円運動の周期\(T\)を計算することができました。また\(ωT=2π\)であるため、\(T=\displaystyle\frac{2πm}{qB}\)を利用することで角速度\(ω\)を計算できます。
\(ωT=2π\)
\(ω×\displaystyle\frac{2πm}{qB}=2π\)
\(ω=\displaystyle\frac{qB}{m}\)
それでは、\(T=\displaystyle\frac{2πm}{qB}\)と\(ω=\displaystyle\frac{qB}{m}\)からわかることは何でしょうか。円周率\(π\)は定数であり、荷電粒子によって電荷量\(q\)と質量\(m\)は決まっています。電束密度\(B\)についても、一様の磁場であれば値は変化しません。
つまり、周期と角速度は荷電粒子の種類と磁場(磁束密度)によって決まる定数です。円運動の半径\(r\)は関係がありません。そのため円の半径が大きくても小さくても、荷電粒子が一周するために必要な時間は同じです。
なお、先ほど計算した答えを暗記しても意味がありません。ここまで解説した方法を理解し、計算によって式を導き出せるようになりましょう。
ローレンツ力に関する練習問題
それでは、ローレンツ力に関する練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 静止している質量\(m\)の粒子について、電圧\(V\)かけて加速させました。その後、粒子はスリット1を通過し、半円を描いた後にスリット2から出てきました。なお粒子の電気量を\(q\)、スリット内の磁束密度を\(B\)、円周率を\(π\)とします。
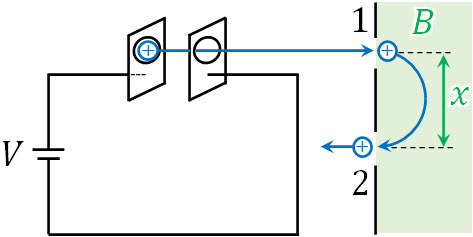
- 加速後の粒子の速さはいくらですか。
- 電圧\(V\)を利用して、スリット1とスリット2の距離\(x\)を求めましょう。
- 粒子がスリット1に入り、スリット2から出てくるまでの時間はいくらですか。
1) 加速後の粒子の速さはいくらですか
力学的エネルギー保存則を利用して式を作りましょう。静電気力の位置エネルギーは\(U=qV\)です。位置エネルギーがすべて運動エネルギーに変わるため、求める速度を\(v\)とすると以下の式になります。
\(qV=\displaystyle\frac{1}{2}mv^2\)
\(v=\sqrt{\displaystyle\frac{2qV}{m}}\)
こうして、\(v=\sqrt{\displaystyle\frac{2qV}{m}}\)とわかりました。
2) 電圧\(V\)を利用して、スリット1とスリット2の距離\(x\)を求めましょう
荷電粒子が磁場から垂直に力を受ける場合、等速円運動をします。荷電粒子によるローレンツ力は\(f=qvB\)です。また円の半径を\(r\)とすると、円運動による向心力\(f\)は\(f=m\displaystyle\frac{v^2}{r}\)です。ローレンツ力と向心力は等しいため、以下の運動方程式を作りましょう。
\(qvB=m\displaystyle\frac{v^2}{r}\)
\(r=\displaystyle\frac{mv}{qB}\)
\(r=\displaystyle\frac{m}{qB}×\sqrt{\displaystyle\frac{2qV}{m}}\)
\(r=\displaystyle\frac{1}{B}\sqrt{\displaystyle\frac{2mV}{q}}\)
なお、\(x=2r\)です。そのため、\(x=\displaystyle\frac{2}{B}\sqrt{\displaystyle\frac{2mV}{q}}\)です。
3) 粒子がスリット1に入り、スリット2から出てくるまでの時間はいくらですか
周期\(T\)を得ることができれば、円運動によって一周する時間がわかります。そこで、周期を計算しましょう。
先ほど解説した通り\(ωT=2π\)であり、\(ω=\displaystyle\frac{v}{r}\)です。そのため、以下のように計算できます。
\(ωT=2π\)
\(\displaystyle\frac{v}{r}×T=2π\)
\(T=\displaystyle\frac{2πr}{v}\)
\(T=2π×\displaystyle\frac{1}{B}\sqrt{\displaystyle\frac{2mV}{q}}×\sqrt{\displaystyle\frac{m}{2qV}}\)
\(T=\displaystyle\frac{2πm}{qB}\)
図より、周期\(T\)の半分を計算することによって、粒子がスリット1からスリット2へ移動するときの時間を得られます。
\(\displaystyle\frac{T}{2}=\displaystyle\frac{πm}{qB}\)
こうして、答えは\(\displaystyle\frac{πm}{qB}\)とわかりました。
角度θにて、速さ\(v\)で磁束密度\(B\)の影響を受けるときの様子
それでは、一様な磁場(一様な磁束密度)の条件で速さ\(v\)の粒子が角度θで磁場内に入るとき、どのような様子になるか学びましょう。例えば以下の図の状況では、磁場(磁束密度\(B\))に対して垂直な成分が\(vsinθ\)であり、平行な成分が\(vcosθ\)となります。
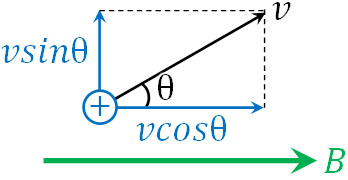
垂直方向の速さが\(vsinθ\)であるため、先ほどの計算で利用した\(v\)を\(vsinθ\)に変えると、等速円運動での計算が可能です。
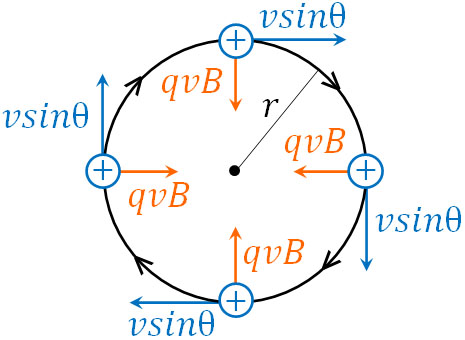
一方、磁場(磁束密度)に対して平行な成分についてはどのように考えればいいのでしょうか。磁場に対して平行な場合、力は加わりません。そのため\(vcosθ\)の成分に対して力が加わることはなく、等速運動となります。
つまり、荷電粒子は\(vcosθ\)の速さで磁束密度\(B\)と平行に移動し、さらには磁場(磁束密度)に対して垂直方向に等速円運動をします。その結果、荷電粒子はらせん運動をします。
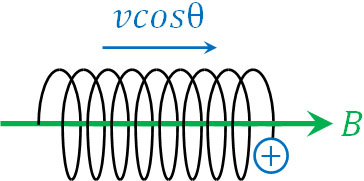
荷電粒子が斜めに磁場へ入ってくる場合であっても、垂直成分と水平成分へ分ければ問題なく計算できます。
粒子に着目し、ローレンツ力を計算する
自由電子を含め、粒子に着目することで力を計算するケースがあります。磁場(磁束密度)が荷電粒子に対して与える力がローレンツ力です。
ローレンツ力を計算するとき、公式を利用しましょう。磁束密度\(B\)に加えて、粒子の電荷\(q\)と速さ\(v\)を利用することでローレンツ力を計算できます。また、ローレンツ力の向きはフレミングの左手の法則によって判断できます。
注意点として、荷電粒子の符号が正なのか、それとも負なのかを確認しましょう。粒子が正に荷電している場合、電流と向きが同じです。一方、電子のような負の電荷では、粒子が動く向きとは反対方向に電流が流れます。
また磁場が加わっている中で荷電粒子が進む場合、等速円運動をします。そこで、等速円運動の内容を復習しましょう。電気と力学を学ぶことにより、理解できる内容がローレンツ力です。






