物理で波動を学ぶとき、ニュートンリングを利用するときの波の干渉条件を習います。ニュートンリングに関する問題を解くとき、近似を利用することになるため、解き方を知っていないと答えを得ることができません。
波の干渉条件は公式を暗記しても意味がありません。そのためニュートンリングを学ぶとき、公式の導出や波が干渉するときの原理を理解しましょう。
ニュートンリングでは位相のずれや近似、波長の変化など、考えるべき点が多いです。ただ問題の解き方は決まっていますし、原理を理解すれば容易に答えを得ることができます。
それでは、どのようにニュートンリングに関する答えを得ればいいのでしょうか。ニュートンリングでの公式の意味や干渉条件の出し方について、練習問題を含めて解説していきます。
もくじ
くさび形空気層とニュートンリングは考え方が同じ
波の干渉では、くさび形空気層を学びます。ニュートンリングというのは、くさび形空気層と考え方がまったく同じです。くさび形空気層でもニュートンリングでも、2枚のガラスを利用することによって波の干渉条件を計算します。
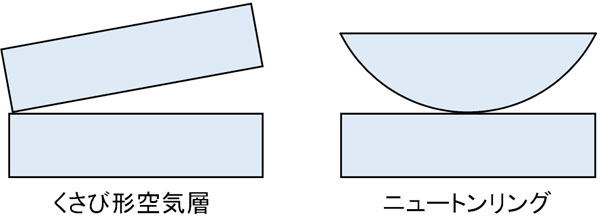
そのためくさび形空気層を理解している場合、ニュートンリングを理解するのは容易です。両者は原理が同じだからです。
ニュートンリングでは、板ガラスの上に球面のガラスを乗せます。なお上からニュートンリングを確認すると、干渉によって同心円状の模様が表れます。

光の干渉により、縞模様が表れると理解しましょう。なおヤングの実験や回折格子、くさび形空気層とは異なり、明線と暗線の間隔は一定ではありません。
ニュートンリングでの光路差は近似を利用する
それでは、ニュートンリングでの光路差を計算しましょう。2つの光の経路差(光路差)を計算する方法は前述の通り、くさび形空気層と同じです。そこで以下の図を作り、2つの光の光路差を求めましょう。
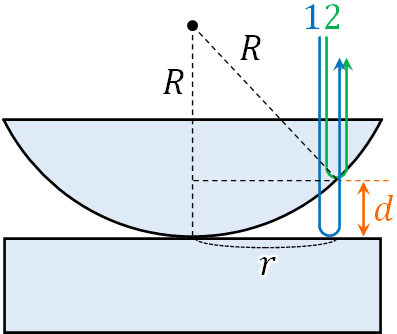
円の半径は\(R\)であり、板の中心から光の反射場所までの距離は\(r\)です。また、上のガラスと下のガラスの距離は\(d\)です。図より、2つの光の経路差は\(2d\)です。そこで三平方の定理を利用して、以下のように計算しましょう。
\(R^2=(R-d)^2+r^2\)
\(R^2=R^2-2Rd+d^2+r^2\)
\(2Rd=d^2+r^2\)
\(2d=\displaystyle\frac{d^2}{R}+\displaystyle\frac{r^2}{R}\)
こうして、光路差\(2d\)は\(\displaystyle\frac{d^2}{R}+\displaystyle\frac{r^2}{R}\)とわかりました。
・近似を利用し、\(\displaystyle\frac{d^2}{R}\)を無視する
ニュートンリングで光の経路差を計算するとき、重要な方法に近似があります。ニュートンリングを利用するとき、\(d\)の値は\(R\)や\(r\)に比べて非常に小さいです。また\(d\)を二乗する場合、得られる値はより小さくなります。
つまり\(\displaystyle\frac{d^2}{R}\)と\(\displaystyle\frac{r^2}{R}\)を比べると、\(\displaystyle\frac{d^2}{R}\)は非常に小さい値であるため、無視できます。そこで近似を利用し、\(\displaystyle\frac{d^2}{R}\)を無視することで以下のように式を変えましょう。
- \(2d=\displaystyle\frac{r^2}{R}\)
こうして、光路差\(2d\)は\(\displaystyle\frac{r^2}{R}\)となります。
屈折率の違いにより、位相がずれる
薄膜やくさび形空気層、ニュートンリングを含め、屈折率の異なる媒質を光が通る場合、反射による位相のずれを考慮しなければいけません。
空気からガラスなど、屈折率の高い媒質へ進む過程で光が反射する場合、固定端反射になることで位相が逆になることが知られています。一方でガラスから空気など、屈折率の低い媒質へ進む過程で光が反射する場合、自由端反射によって位相は変化しません。
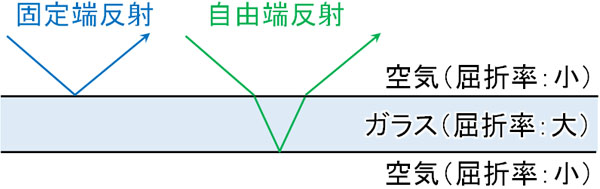
そこでニュートンリングでの反射を確認しましょう。空気中(真空中)では屈折率が1です。それに対して、ガラスは空気よりも必ず屈折率が高くなります。そのため、以下のようになります。
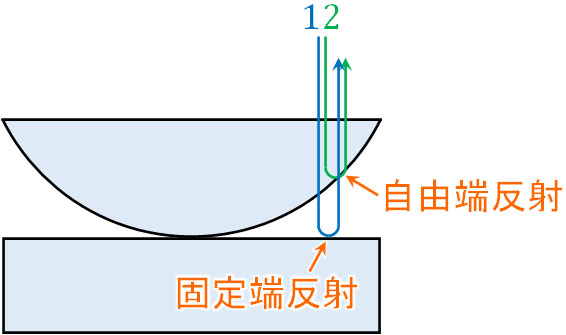
こうして、2つの光は逆位相になります。明線条件や暗線条件を作るとき、2つの波は同位相ではないことを考慮しましょう。この点について、くさび形空気層と考え方は同じです。
ニュートンリングでの明線条件と暗線条件
それでは、ここまで解説した知識を利用してニュートンリングでの明線条件と暗線条件を出しましょう。前述の通り、光の経路差\(2d\)は\(\displaystyle\frac{r^2}{R}\)です。
2つの光は逆位相であるため、半波長の奇数倍であれば強め合うことで明線になります。一方、半波長の偶数倍であれば弱め合うことで暗線になります。そのため、以下の式を作れます。
【強め合う条件(明線の条件)】
- \(\displaystyle\frac{r^2}{R}=\displaystyle\frac{λ}{2}×(2m+1)\)(\(m=0,1,2…\))
【弱め合う条件(暗線の条件)】
- \(\displaystyle\frac{r^2}{R}=\displaystyle\frac{λ}{2}×2m\)(\(m=0,1,2…\))
こうして、明線と暗線の条件を得ることができました。暗記しても問題を解くことはできないため、この式を計算によって出せるようにしましょう。
また式を確認すると、明線や暗線の条件では、中心からの距離が\(r^2\)に比例するとわかります。これが、ニュートンリングで明線の間隔(または暗線の間隔)が等間隔にならない理由です。
ニュートンリングの中心Oは明るいか、それとも暗いか
先ほど得た公式を利用して、ニュートンリングの中心Oが明るくなるのか、それとも暗くなるのかを確認しましょう。ニュートンリングの中心では、\(r=0\)になります。そこで、それぞれの式に\(r=0\)を代入しましょう。
【強め合う条件(明線の条件)】
- \(0=\displaystyle\frac{λ}{2}×(2m+1)\)(\(m=0,1,2…\))
【弱め合う条件(暗線の条件)】
- \(0=\displaystyle\frac{λ}{2}×2m\)(\(m=0,1,2…\))
これらの式のうち式を満たせるのは、波が弱め合うときのみです。明線では、\(m\)にどの整数を代入しても左辺が0になりません。一方で暗線条件では、\(m=0\)のときに左辺が0になります。そのため、ニュートンリングの中心Oは暗くなるとわかります。
波長を変える場合、明線と暗線の間隔が変化する
次に、光の条件を変えてみましょう。可視光では、色によって波長が異なります。赤色では波長が長く、青色(または紫色)では波長が短くなります。
それでは、波長\(λ\)の赤色の光を利用して観測していた実験について、青色の光に変える場合、明線の間隔はどのように変化するでしょうか。
まず、暗線の条件を\(r\)にそろえましょう(明線よりも暗線のほうが計算しやすいため、暗線条件を利用します)。
\(\displaystyle\frac{r^2}{R}=\displaystyle\frac{λ}{2}×2m\)
\(r^2=λmR\)
\(r=\sqrt{λmR}\)
暗線の間隔\(Δr\)を出したいため、\(m+1\)番目から\(m\)を引きましょう。
\(Δr=\sqrt{λR(m+1)}-\sqrt{λmR}\)
\(Δr=\sqrt{λR}(\sqrt{m+1}-\sqrt{m})\)
式を見てわかる通り、\(λ\)の値が小さくなると、暗線の間隔\(Δr\)は小さくなることがわかります。そのため赤色のレーザーから青色のレーザーに変える場合、波長が小さくなるので暗線の間隔は短くなります。当然、明線の間隔も短くなります。
下から光を当てる場合(下から見る場合)の縞模様の表れ方
くさび形空気層と同じように、ニュートンリングでは下から光を当てる場合(または下から見る場合)に縞模様がどのように表れるのか問われることもあります。
下から光を当て、上からニュートンリングを確認する場合、2つの光の経路差に変化はありません。ただ光の反射での位相が変化します。
以下のように光1はガラスを透過するので位相の変化はありません。一方で光2は二カ所で反射します。反射するとき、両方とも空気からガラスへ進む過程での反射です。そのため2回の固定端反射をするため、位相の変化はありません。つまり、2つの光は同位相になります。
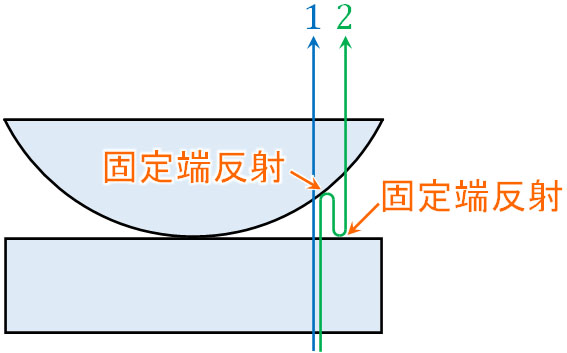
経路差は同じであるものの、2つの光は逆位相から同位相へと変化します。つまり、明線条件と暗線条件は以下のように変化します。
【強め合う条件(明線の条件)】
- \(\displaystyle\frac{r^2}{R}=\displaystyle\frac{λ}{2}×2m\)(\(m=0,1,2…\))
【弱め合う条件(暗線の条件)】
- \(\displaystyle\frac{r^2}{R}=\displaystyle\frac{λ}{2}×(2m+1)\)(\(m=0,1,2…\))
こうして、同心円状の縞模様について明暗の線が逆転します。なお下から光を当てて上から模様を確認する場合であっても、上から光を当てて下から光を確認する場合であっても公式の計算方法は同じです。
水など、液体を満たす場合の考え方
なおくさび形空気層でもニュートンリングでも、水を満たす場合の計算問題を問われることが多いです。そこで2枚のガラスを用いる波の干渉について、液体を利用する場合の計算を行えるようにしましょう。
例えば ガラスとレンズの間を屈折率\(n_1\)の水で満たす場合、暗線の間隔はどのように変化するでしょうか。なお、水の屈折率\(n_1\)とガラスの屈折率\(n\)の関係は\(1<n_1<n\)とします。
ニュートンリングで水を満たす場合の問題を解くことができれば、くさび形空気層で水を満たす場合の問題も解くことができます。考え方は共通しているからです。今回はニュートンリングで液体を満たす場合の計算をしてみましょう。
まず、位相のずれを確認しましょう。2枚のガラスの間が水で満たされている場合であっても、\(1<n_1<n\)であるため、位相のずれは同じです。つまり、2つの光は逆位相の関係です。
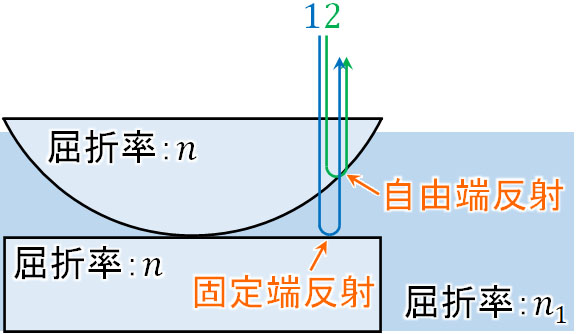
ただ光は水を通るため、光路差が変化します。光路差は経路差と屈折率をかけることで得られます。そのため経路差が\(2d\)の場合、水で満たすときの光路差は\(2dn_1\)となります。
なお液体がない場合、光の経路差\(2d\)は\(\displaystyle\frac{r^2}{R}\)です。そのため水を満たす場合、光路差\(2dn_1\)は\(\displaystyle\frac{n_1r^2}{R}\)となります。そのため、以下の明線条件と暗線条件を作ることができます。
【強め合う条件(明線の条件)】
- \(\displaystyle\frac{n_1r^2}{R}=\displaystyle\frac{λ}{2}×(2m+1)\)(\(m=0,1,2…\))
【弱め合う条件(暗線の条件)】
- \(\displaystyle\frac{n_1r^2}{R}=\displaystyle\frac{λ}{2}×2m\)(\(m=0,1,2…\))
こうして、波が強め合うときと弱め合うときの条件を計算できました。
・暗線の間隔\(Δr\)の変化はどうなるのか
それでは水を満たす場合、暗線の間隔がどのように変化するのか確認しましょう。先ほどと同じように、\(m+1\)番目から\(m\)番目を引くことによって暗線の間隔\(Δr\)を出します。まず、\(r\)の式を作りましょう。
\(\displaystyle\frac{n_1r^2}{R}=\displaystyle\frac{λ}{2}×2m\)
\(r^2=\displaystyle\frac{λRm}{n_1}\)
\(r=\sqrt{\displaystyle\frac{λRm}{n_1}}\)
次に、\(m+1\)番目から\(m\)番目を引きます。
\(Δr=\sqrt{\displaystyle\frac{λR(m+1)}{n_1}}-\sqrt{\displaystyle\frac{λRm}{n_1}}\)
\(Δr=\sqrt{\displaystyle\frac{λR}{n_1}}(\sqrt{m+1}-\sqrt{m})\)
空気の屈折率は1であるため、水の屈折率\(n_1\)は1よりも値が大きいです。また分母に\(n_1\)があるため、暗線の間隔\(Δr\)は短くなるとわかります。このように数式を得ることによって、水を満たすことによる暗線間隔の違いを確認できました。
ニュートンリングでの光の干渉を学ぶ
ニュートンリングで起こる波の干渉を学ぶとき、薄膜での干渉やくさび形空気層を事前に理解しておく必要があります。これらの内容を理解している場合、ニュートンリングで明線条件と暗線条件を得るのは簡単です。
くさび形空気層とニュートンリングは原理が同じです。光の経路差を得る方法は異なるものの、基本的な概念は共通しているのです。そこで、干渉条件を利用することで明線(または暗線)の間隔や波長の変化を計算できるようになりましょう。
また水などの液体を満たす場合、光路差を考慮しなければいけません。そこで薄膜での干渉と同様に、経路差と屈折率をかけることによって光路差を計算しましょう。
波の干渉の応用問題がニュートンリングです。干渉条件を得るときは近似を利用するため、計算方法を知っていないと答えを得ることはできません。ただ干渉条件を得る過程を学んでいる場合、ニュートンリングに関する問題を解けるようになります。






