線対称・点と直線の距離：公式の利用と計算方法

点と直線の距離を計算できるようになることは重要です。このとき重要な概念が線対称です。直線に対して対称な点を得るとき、どのような条件が成立するのか理解しなければいけません。

なお2つの点が線対称の場合、2点と直線との距離は同じです。そのため線対称を利用することによって、距離を計算できるようになることは多いです。

また点と直線の距離を計算するとき、公式を利用しましょう。公式の証明は複雑なので公式を覚える必要があるものの、公式を利用すれば点と直線の距離を容易に計算できます。

それでは、直線に対して対称な点となる条件には何があるのでしょうか。また点と直線の距離を得る公式を利用して計算するには、どのようにすればいいのでしょうか。点と直線の距離を得る方法について、例題を含めて公式の利用法を解説していきます。

1 直線に対して対称な点の条件
- 1.1 折れ線の長さの最小値を計算する
2 点と直線の距離を求める公式
- 2.1 公式を利用して点と直線の距離を計算する
- 2.2 曲線上の点と直線との距離
3 対称となる場合の条件を利用し、点と直線の距離を得る

直線に対して対称な点の条件

特定の直線に対して、対称関係にある点を得るにはどうすればいいでしょうか。例えば、下図のように直線\(l\)に対して点Pと点Qが対称関係にあるとします。この場合、以下の2つの条件を満たします。

直線\(l\)とPQは垂直：\(l⊥PQ\)
線分PQの中点は\(l\)上に存在する

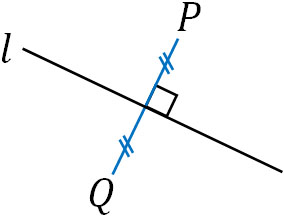
この性質を利用して、以下の問題を解きましょう。

\(x+y-1=0\)に対して、点P\((3,2)\)と対称な点Qの座標を求めましょう。

点Qの座標を\((a,b)\)とします。直線とPQは垂直で交わるため、それぞれの傾きをかけると-1になります。\(x+y-1=0\)の傾きは-1であるため、以下の式を作れます。

\(-1×\displaystyle\frac{b-2}{a-3}=-1\)

\(b-2=a-3\)

\(b=a-1\)

また、線分PQの中点は\(l\)上に存在します。線分PQの中点の座標は\(\left(\displaystyle\frac{a+3}{2},\displaystyle\frac{b+2}{2}\right)\)です。そのため、この座標を直線\(l\)の方程式\(x+y-1=0\)に代入することができます。そこで、以下のように式を作りましょう。

\(\displaystyle\frac{a+3}{2}+\displaystyle\frac{b+2}{2}-1=0\)

\((a+3)+(b+2)-2=0\)

\(a+b+3=0\)

\(b=a-1\)と\(a+b+3=0\)の両方を満たす値が答えです。そこで、\(b=a-1\)を\(a+b+3=0\)に代入しましょう。

\(a+(a-1)+3=0\)

\(a=-1\)

\(a=-1\)であるため、\(b=-2\)です。そのため、点Qの座標は\((-1,-2)\)であるとわかりました。

折れ線の長さの最小値を計算する

直線に対して対称な点を利用すると、問題を解けることが多いです。例えば、折れ線の長さの最小値を計算したい場合、対称な点を利用しましょう。

以下のように直線\(l\)があります。点Pを通り、点Aと点Bの距離が最小となるときの点Pの座標を求めるにはどうすればいいでしょうか。

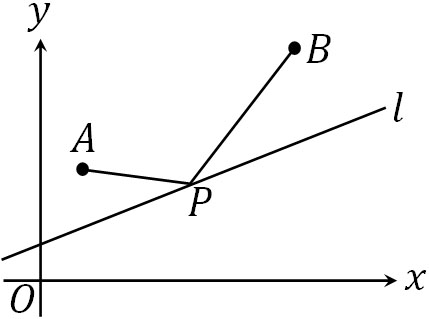
\(AP+PB\)を計算するのは大変です。そこで、直線に対して対称な点A’を以下のように作りましょう。

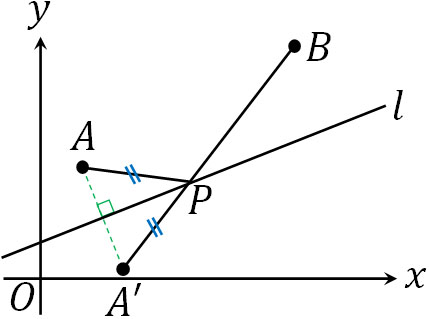
APとAP’の距離は同じです。また\(AP+PB\)が最小値となる場合、A’Bは直線になります。そこで、A’、P、Bが一直線上に存在するときの条件を計算しましょう。これにより、折れ線の長さの最小値を得ることができます。

それでは、以下の問題の答えは何でしょうか。

2点A\((1,6)\)とB\((5,3)\)があります。点Pが直線\(l:y=-x+5\)上を動くとき、\(AP+PB\)が最小値となる点Pの座標を求めましょう。

図を作ると、点Aと点Bは直線\(l\)に対して同じ側に存在します。そこで、直線に対して対称となる点B’\((a,b)\)を取りましょう。

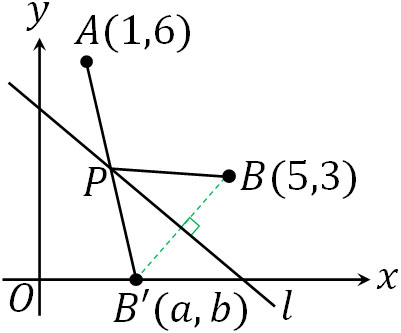
まず、B’の座標を計算します。BB’の中点は\(\left(\displaystyle\frac{5+a}{2},\displaystyle\frac{3+b}{2}\right)\)です。中点は\(l\)上に存在するため、方程式\(y=-x+5\)を満たします。そのため、以下のように代入しましょう。

\(y=-x+5\)

\(\displaystyle\frac{3+b}{2}=-\displaystyle\frac{5+a}{2}+5\)

\(3+b=-(5+a)+10\)

\(b=-a+2\)

また\(y=-x+5\)の傾きは-1であり、BB’の傾きは\(\displaystyle\frac{3-b}{5-a}\)です。垂直関係では2つの傾きをかけると-1になるため、以下のように計算しましょう。

\(-1×\displaystyle\frac{3-b}{5-a}=-1\)

\(3-b=5-a\)

\(b-a+2=0\)

そこで、\(b=-a+2\)を\(b-a+2=0\)に代入しましょう。

\((-a+2)-a+2=0\)

\(a=2\)

\(a=2\)であるため、\(b=0\)です。つまり、B’の座標は\((2,0)\)とわかりました。そこで、点Aと点B’を結ぶ直線の方程式を計算しましょう。任意の点P\((x,y)\)について、APとAB’は傾きが同じであるため、以下の式を作れます。

\(\displaystyle\frac{y-6}{x-1}=\displaystyle\frac{0-6}{2-1}\)

\(y-6=-6(x-1)\)

\(y=-6x+12\)

こうして、直線AB’の方程式は\(y=-6x+12\)であるとわかりました。また、点PはAB’上だけでなく、直線\(l\)上にも存在します。そこで、直線AB’と直線\(l\)の交点を計算しましょう。

\(y=-x+5\)

\(-6x+12=-x+5\)

\(-5x=-7\)

\(x=\displaystyle\frac{7}{5}\)

\(x=\displaystyle\frac{7}{5}\)であるため、\(y=\displaystyle\frac{18}{5}\)です。こうして、点Pの座標は\(\left(\displaystyle\frac{7}{5},\displaystyle\frac{18}{5}\right)\)とわかりました。

点と直線の距離を求める公式

それでは、点と直線の距離はどのように計算すればいいのでしょうか。点\((x_1,y_1)\)と直線\(ax+by+c=0\)の距離\(d\)は以下の公式によって計算できます。

\(d=\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)

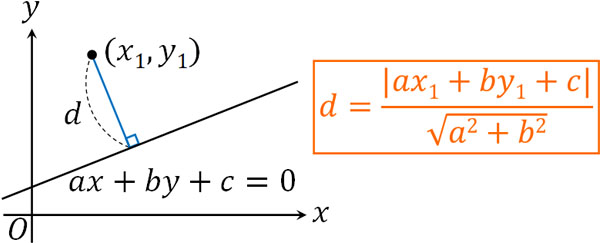
この公式を証明するのは大変であるため、ここでは証明の解説をしません。また、この公式は暗記しましょう。

公式を利用して点と直線の距離を計算する

公式を利用できるようになるため、実際に練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

直線\(y=-x+4\)と点\((4,6)\)の距離を求めましょう。

\(y=-x+4\)を変形すると\(x+y-4=0\)です。そこで、\(x+y-4=0\)を利用して公式に当てはめましょう。点の座標は\((4,6)\)であるため、距離\(d\)は以下のようになります。

\(d=\displaystyle\frac{|4+6-4|}{\sqrt{1^2+1^2}}\)

\(d=\displaystyle\frac{6}{\sqrt{2}}\)

\(d=3\sqrt{2}\)

こうして、距離は\(3\sqrt{2}\)とわかりました。

曲線上の点と直線との距離

それでは曲線上を点が動く場合、直線との距離はどのように計算すればいいのでしょうか。直線と点の距離は先ほど解説した公式を利用すればいいため、公式を用いて計算しましょう。それでは、以下の問題の答えは何でしょうか。

2点A\((0,-1)\)とB\((2,1)\)があります。点Pが\(y=x^2\)の上を動くとき、△ABPの面積が最小となる点Pの座標を求めましょう。

点Pの\(x\)座標を\(t\)とすると、点Pの座標は\((t,t^2)\)です。また△ABPの面積が最小となるためには、下図の高さ\(h\)が最小になればいいとわかります。

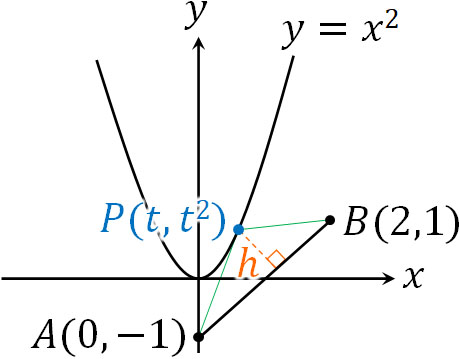
つまり、点Pと直線ABの距離が最小になる値を計算すればいいです。公式を利用するため、まずは直線ABの方程式を計算しましょう。以下のようになります。

\(\displaystyle\frac{y-(-1)}{x-0}=\displaystyle\frac{1-(-1)}{2-0}\)

\(y+1=x\)

\(x-y-1=0\)

次に、直線\(x-y-1=0\)と点P\((t,t^2)\)との距離（三角形の高さ）\(h\)を計算しましょう。

\(h=\displaystyle\frac{|t-t^2-1|}{\sqrt{1^2+(-1)^2}}\)

\(h=\displaystyle\frac{1}{\sqrt{2}}|-(t^2-t)-1|\)

\(h=\displaystyle\frac{1}{\sqrt{2}}\left|-\left(t-\displaystyle\frac{1}{2}\right)^2-\displaystyle\frac{3}{4}\right|\)

\(h=\displaystyle\frac{1}{\sqrt{2}}\left(t-\displaystyle\frac{1}{2}\right)^2+\displaystyle\frac{3}{4\sqrt{2}}\)

こうして、\(t=\displaystyle\frac{1}{2}\)のときに三角形の高さ\(h\)は最小値\(\displaystyle\frac{3}{4\sqrt{2}}\)になるとわかります。そのため、点Pの座標は\(\left(\displaystyle\frac{1}{2},\displaystyle\frac{1}{4}\right)\)です。