数列の中には、分数を含むケースがあります。調和数列も分数を含むものの、調和数列ではないケースで計算問題を解けるようにならなければいけません。
分数を含む数列の和を計算するとき、部分分数分解の利用を検討しましょう。部分分数分解の公式は重要ではなく、利用場面は少ないです。ただ数列で分数の和を計算するとき、部分分数への分解をすることになります。
このとき、応用問題を解けるようになりましょう。分母に複数の式が含まれていたり、ルートがあったりするとき、数列の和を計算できるようにするのです。
それでは、どのように考えて分数の数列の和を計算すればいいのでしょうか。部分分数分解のやり方を含めて解説していきます。
数列で利用される部分分数への分解
一つの分数式を複数の分数式へ分解する方法に部分分数分解があります。前述の通り重要な公式ではなく、利用できる場面は限られます。ただ分数が含まれる数列の和を計算したい場合、部分分数分解によって計算することを考えましょう。
部分分数分解の公式は以下になります。
- \(\displaystyle\frac{1}{(x+a)(x+b)}\)\(=\displaystyle\frac{1}{b-a}\left(\displaystyle\frac{1}{x+a}-\displaystyle\frac{1}{x+b}\right)\)
以下のように計算することにより、この公式が成り立つとわかります。
\(\displaystyle\frac{1}{b-a}\left(\displaystyle\frac{1}{x+a}-\displaystyle\frac{1}{x+b}\right)\)
\(=\displaystyle\frac{1}{b-a}·\displaystyle\frac{b-a}{(x+a)(x+b)}\)
\(=\displaystyle\frac{1}{(x+a)(x+b)}\)
部分分数分解を利用すれば、例えば以下のように式を変形できます。
- \(\displaystyle\frac{1}{12}=\displaystyle\frac{1}{2·6}=\displaystyle\frac{1}{4}\left(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{6}\right)\)
- \(\displaystyle\frac{1}{x(x+1)}=\displaystyle\frac{1}{x}-\displaystyle\frac{1}{x+1}\)
- \(\displaystyle\frac{1}{x(x+3)}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{x}-\displaystyle\frac{1}{x+3}\right)\)
分数を含む数列では、部分分数分解の公式を利用して計算しましょう。
分数を含む数列では部分分数分解を行う
それでは、どのように計算すればいいのでしょうか。以下の数列の和\(S\)を計算しましょう。
- \(\displaystyle\frac{1}{1·3},\displaystyle\frac{1}{3·5},\displaystyle\frac{1}{5·7},…\)\(,\displaystyle\frac{1}{(2n-1)(2n+1)}\)
この数列について、第\(k\)項は\(\displaystyle\frac{1}{(2k-1)(2k+1)}\)です。そこで、以下のように部分分数分解をしましょう。
\(\displaystyle\frac{1}{(2k-1)(2k+1)}\)
\(=\displaystyle\frac{1}{(2k+1)-(2k-1)}\)\(\left(\displaystyle\frac{1}{2k-1}-\displaystyle\frac{1}{2k+1}\right)\)
\(=\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{2k-1}-\displaystyle\frac{1}{2k+1}\right)\)
それでは、この数列の和はどのようになるでしょうか。以下のように部分分数分解をした後に和を計算すると、ほとんどの分数を消去できます。
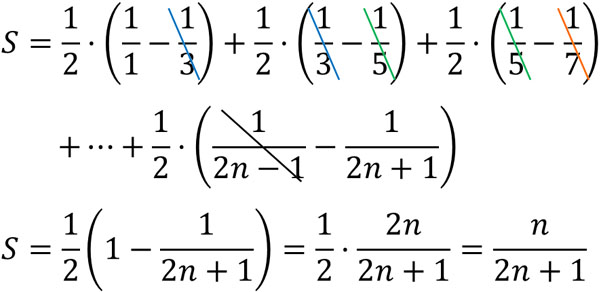
こうして、分数を含む数列の和を計算することができました。部分分数分解を利用することにより、足し算をすると多くの部分を消去できるようになり、結果として答えを得ることができるのです。
分数を含む数列の応用問題
ただ場合によっては、一見すると部分分数分解を利用できないように思ってしまう計算問題があります。この場合、どのように答えを得ればいいのでしょうか。
分数を含む数列の和を計算するとき、部分分数分解を利用する方針は変わりません。実際に練習問題を解くことにより、どのように答えを得ればいいのか学びましょう。以下の数列の和\(S\)はいくらでしょうか。
- \(\displaystyle\frac{1}{1·2·3},\displaystyle\frac{1}{2·3·4},\)\(\displaystyle\frac{1}{3·4·5},\)\(…,\)\(\displaystyle\frac{1}{n(n+1)(n+2)}\)
分母に3つの因数がある場合、前半2つの因数と後半2つの因数を利用し、部分分数分解をします。そこで、以下のように式を変形しましょう。
\(\displaystyle\frac{1}{n(n+1)(n+2)}\)\(=\displaystyle\frac{A}{\color{red}{n(n+1)}}\)\(+\displaystyle\frac{B}{\color{red}{(n+1)(n+2)}}\)
このように、無理やり一つの分数を二つの分数へと分解します。\(A\)と\(B\)に当てはまる数字は不明です。ただ計算することにより、後で\(A\)と\(B\)に当てはまる数を探せばいいです。そこで、以下の計算によって二つの分数を再び一つの分数へ戻しましょう。
\(\displaystyle\frac{A}{n(n+1)}+\displaystyle\frac{B}{(n+1)(n+2)}\)
\(=\displaystyle\frac{(n+2)A+nB}{n(n+1)(n+2)}\)
\(=\displaystyle\frac{(A+B)n+2A}{n(n+1)(n+2)}\)
\(\displaystyle\frac{1}{n(n+1)(n+2)}\)を変形すると、\(\displaystyle\frac{(A+B)n+2A}{n(n+1)(n+2)}\)になる必要があります。言い換えると、\((A+B)n+2A=1\)でなければいけません。つまり、以下の式を作ることができます。
- \(A+B=0\)
- \(2A=1\)
このときを解くと、\(A=\displaystyle\frac{1}{2}\)、\(B=-\displaystyle\frac{1}{2}\)になります。そこで、以下のように式を作りましょう。
\(\displaystyle\frac{A}{n(n+1)}+\displaystyle\frac{B}{(n+1)(n+2)}\)
\(=\displaystyle\frac{1}{2}·\displaystyle\frac{1}{n(n+1)}\)\(-\displaystyle\frac{1}{2}·\displaystyle\frac{1}{(n+1)(n+2)}\)
こうして、以下のように部分分数分解することができました。
\(\displaystyle\frac{1}{n(n+1)(n+2)}\)\(=\displaystyle\frac{1}{2}·\displaystyle\frac{1}{n(n+1)}\)\(-\displaystyle\frac{1}{2}·\displaystyle\frac{1}{(n+1)(n+2)}\)
部分分数へ分解することができたら、これまで説明したやり方と同じ方法で足し算をしましょう。
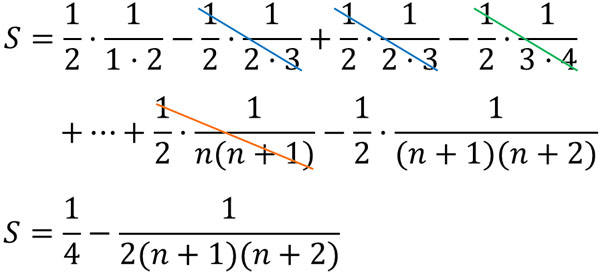
こうして、分数を含む数列の和を計算することができました。
分母にルートを含む場合は有利化を行う
分数を含む数列には、分母にルートを含むケースもあります。この場合は部分分数分解をするのではなく、分母の有利化を行います。ただ、計算するときの基本的な考え方は同じです。
それでは、以下の計算をすることで和\(S\)を求めましょう。
- \(\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{1}{\sqrt{k}+\sqrt{k+1}}}\)
分母の有利化を行うと以下のように計算できます。
\(\displaystyle\frac{1}{\sqrt{k}+\sqrt{k+1}}\)
\(=\displaystyle\frac{1}{\sqrt{k}+\sqrt{k+1}}\)\(×\displaystyle\frac{\sqrt{k}-\sqrt{k+1}}{\sqrt{k}-\sqrt{k+1}}\)
\(=\displaystyle\frac{\sqrt{k}-\sqrt{k+1}}{-1}\)
\(=\sqrt{k+1}-\sqrt{k}\)
そこで、以下のように数列の和\(S\)を計算しましょう。
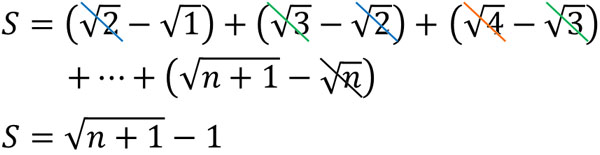
分母の有利化によって、数列の和を得ることができました。
分数を含む数列の和を計算する
特殊な数列の計算方法を理解する必要があり、こうした数列の一つが「分数を含む数列」です。部分分数分解をすることにより、一つの分数を二つの分数へ分解することができます。重要度の低い公式であるものの、分数を含む数列の問題ではひんぱんに利用されます。
また分母に3つの因数を含む場合についても部分分数分解を行いましょう。この分解については、公式を利用するのではなく、強引に部分分数分解をすることによって係数を合わせましょう。
場合によっては、分母にルートを含む式を計算しなければいけないケースもあります。この場合は部分分数分解ではなく、分母の有利化によって数列の和を計算しましょう。
計算方法を理解していないと、分数を含む数列の和を計算することはできません。そこで、どのように答えを得ればいいのか学びましょう。






