関数で学ばなければいけない内容に分数関数と無理関数があります。分数関数と無理関数の基本はどちらも難しい内容ではなく、容易に理解できます。
反比例のグラフについて、平行移動させると分数関数になります。また、ルートを利用した関数は無理関数と呼ばれます。
分数関数でも無理関数でも、問題の解き方は同じです。つまり、これまで学んだ知識を利用すれば問題を解けます。ただ、これまで学んだグラフと少し異なる点もあるため、どのポイントに注意すればいいのか学ばなければいけません。
それでは、分数関数と無理関数はどのようなグラフになるのでしょうか。分数関数と無理関数の基本を解説していきます。
もくじ
分数関数のグラフの形と平行移動
\(x\)を利用して、分数式で表した式を分数関数といいます。そのため、\(y=\displaystyle\frac{1}{x}\)のような反比例のグラフは分数関数です。
最も単純な分数関数は\(y=\displaystyle\frac{k}{x}\)となります(\(k\)は実数)。\(y=\displaystyle\frac{k}{x}\)では、\(x\)軸と\(y\)軸が漸近線(近づくものの、接することのない線)になります。それでは、\(y=\displaystyle\frac{k}{x}\)を平行移動させるとどのようになるでしょうか。
\(y=\displaystyle\frac{k}{x}\)を\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)移動させる場合、式は以下のようになります。
- \(y=\displaystyle\frac{k}{x-p}+q\)
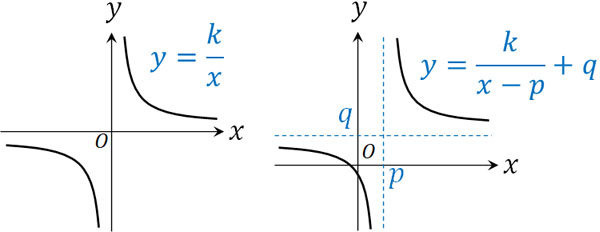
関数の平行移動は既に学んでいると思うので、平行移動させるとき、このように変形できるのは問題なく理解できると思います。
分数関数のグラフを描く
それでは、分数関数のグラフを描けるようになりましょう。以下の分数関数はどのようなグラフを描けるでしょうか。
- \(y=\displaystyle\frac{x+8}{x+3}\)
分数関数のグラフを描くとき、式を\(y=\displaystyle\frac{k}{x-p}+q\)の形へ変形しましょう。
\(y=\displaystyle\frac{x+8}{x+3}\)
\(y=\displaystyle\frac{(x+3)+5}{x+3}\)
\(y=\displaystyle\frac{5}{x+3}+1\)
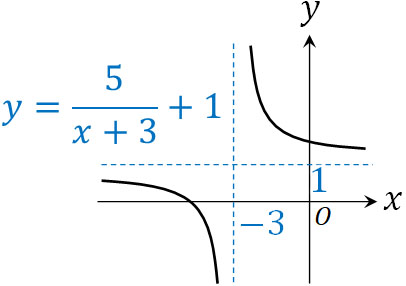
\(y=\displaystyle\frac{5}{x}\)のグラフに対して、\(x\)軸方向に\(-3\)、\(y\)軸方向に\(1\)移動させると\(y=\displaystyle\frac{5}{x+3}+1\)のグラフになります。
ルートを用いる無理関数のグラフと範囲
次に無理関数を学びましょう。\(y=\sqrt{x}\)や\(y=\sqrt{3x+1}\)のように、ルートの中に文字が存在する関数を無理関数といいます。例えば\(y=\sqrt{x}\)は以下のグラフになります。
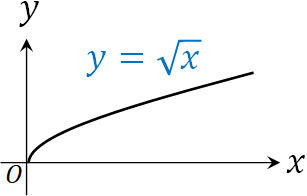
このグラフを見てわかる通り、無理関数は放物線となるとわかります。\(y=\sqrt{x}\)を二乗すると\(y^2=x\)となります。また、\(x\)と\(y\)を入れ替えると\(y=x^2\)となります。このように式を確認することによっても、\(y=\sqrt{x}\)のグラフは放物線になると理解できます。
ただ、無理関数ではルート内が必ずプラスにならなければいけません。そのため一般的な放物線とは異なり、無理関数のグラフは放物線の片方半分となります。
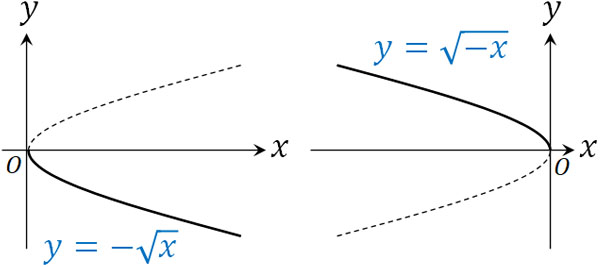
なおルートの前にマイナスが加わる場合、グラフは下半分になります。またルートの中にマイナスが存在する場合、グラフは左側に描かれるようになります。
それでは、平行移動させる場合はどのようにすればいいのでしょうか。無理関数を\(y=\sqrt{ax}\)(\(a≠0\))と表せば、グラフの拡大と縮小が可能です。また、\(y=\sqrt{a(x-p)}\)は\(y=\sqrt{ax}\)のグラフを\(x\)軸方向へ\(p\)移動させることを意味します。
なお無理関数を\(y=\sqrt{ax+b}\)と記すことは多いです。この場合、式を\(y=\sqrt{a(x-p)}\)へ変形することでグラフを描くようにしましょう。
無理関数のグラフと直線との共有点
それでは、無理関数のグラフと直線の共有点を計算してみましょう。以下の問題の答えは何でしょうか。
- \(y=\sqrt{2x+2}\)と\(y=x-3\)の共有点の座標を求めましょう。
代入することで以下のように計算しましょう。
\(y=\sqrt{2x+2}\)
\(x-3=\sqrt{2x+2}\)
\((x-3)^2=2x+2\)
\(x^2-8x+7=0\)
\((x-7)(x-1)=0\)
\(x=1,7\)
ただ、\(x=1,7\)が答えではありません。図を描くと以下のようになります。

下半分にグラフが存在する場合、\((1,-2)\)は交点です。ただ実際には下半分にグラフが存在しないため、交点は\((7,4)\)のみです。無理関数ではグラフの範囲を確認して答えを得ましょう。
無理方程式の実数解の個数と判別式の利用
次に、無理方程式の実数解の個数を計算しましょう。二次関数を用いて実数解の個数を得たことがある場合、同じ方法によって答えを得ることができます。ただ前述の通り、無理関数では上半分または下半分のグラフになるため、これを考慮しましょう。以下の問題の答えは何でしょうか。
- \(\sqrt{2x-1}=x+k\)について、実数解の個数を求めましょう。
以下のように計算しましょう。
\(\sqrt{2x-1}=x+k\)
\(2x-1=(x+k)^2\)
\(x^2+(2k-2)x+k^2+1=0\)
判別式を利用することにより、実数解の個数を得ることができます。例えば重解をもつ場合を調べるとき、判別式\(D\)がゼロになる場合を計算します。
\(\displaystyle\frac{D}{4}=(k-1)^2-k^2-1=0\)
\(-2k=0\)
\(k=0\)
つまり\(k=0\)のとき、重解となり、答えは1つです。
ただ\(y=\sqrt{2x-1}\)のグラフは下半分がないため、この事実を考慮しなければいけません。\(y=\sqrt{2x-1}\)について、\(y\)の値が0のとき、\(x\)の値は\(\displaystyle\frac{1}{2}\)です。そこで、\(y=x+k\)が\(\left(\displaystyle\frac{1}{2},0\right)\)を通るケースを考えましょう。この場合、\(k=-\displaystyle\frac{1}{2}\)です。
グラフを描くと以下のようになります。
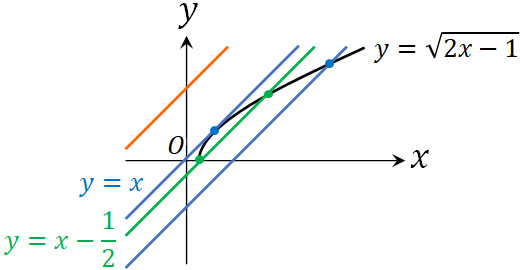
\(k\)の値が変化すると、直線\(y=x+k\)の切片の値が変化します。そのためグラフより、答えは以下になるとわかります。
- \(k>0\)のとき、実数解は0
- \(k=0\)または\(k<-\displaystyle\frac{1}{2}\)のとき、実数解は1
- \(-\displaystyle\frac{1}{2}≦k<0\)のとき、実数解は2
こうして、答えを得ることができました。判別式を用いて計算する必要はあるものの、放物線の計算とは答えの出し方が少し異なります。
分数関数と無理関数の基本を学ぶ
少し特殊な関数に分数関数と無理関数があります。関数を学ぶとき、これらの関数は基本的な内容であり、難しい内容ではありません。
反比例のグラフをすでに学んでおり、反比例のグラフは分数関数を指します。そこで、反比例のグラフを平行移動させるときの式を判断できるようになりましょう。
また、根号を利用して文字を表すこともあります。無理関数ではルート内の値がプラスになる必要があるため、放物線の片側一方が存在しません。そこで範囲を確認することで答えを計算しましょう。
少し計算方法は異なるものの、これまで学んだ関数の知識を利用すれば分数関数であっても無理関数であっても問題を解くことができます。






