無限等比数列の極限：収束条件と漸化式・不等式の利用

等比数列に関する無限数列を無限等比数列といいます。無限等比数列の極限を計算するとき、公比\(r\)によって値が収束するのか、それとも発散するのかが変わります。

無限等比数列を計算するとき、式を変形しましょう。これにより、0になる値や無限大になる値を確認するのです。直感で答えを得ることはできないため、割り算や場合分けによって答えを得るのです。

なお無限等比数列の計算では、漸化式を利用することもあります。漸化式の計算をした後、数列の極限を確認することによって答えを得ましょう。なお場合によっては、はさみうちの原理を利用することによって計算しなければいけないこともあります。

それでは、どのように無限等比数列の計算をすればいいのでしょうか。無限等比数列の計算方法を解説していきます。

1 公比\(r\)によって変化する無限等比数列の極限
- 1.1 無限等比数列の極限を計算する
- 1.2 無限等比数列の収束条件
2 隣接2項間の漸化式と極限
- 2.1 はさみうちの原理を利用する漸化式と極限
3 無限等比数列の性質と漸化式の関係を学ぶ

公比\(r\)によって変化する無限等比数列の極限

無限等比数列で得られる答えは公比\(r\)によって変化します。具体的には、無限等比数列\(r^n\)の極限は以下のようになります。

\(r>1\)の場合：\(\displaystyle \lim_{ n \to \infty } r^n=∞\)
\(r=1\)の場合：\(\displaystyle \lim_{ n \to \infty } r^n=1\)
\(|r|<1\)の場合：\(\displaystyle \lim_{ n \to \infty } r^n=0\)
\(r≦-1\)の場合：\(\displaystyle \lim_{ n \to \infty } r^n\)は振動する

\(r>1\)の場合の場合、当然ながら無限大に値は大きくなります。また\(\displaystyle \lim_{ n \to \infty } 1^n=1\)となりますし、\(|r|<1\)で\(\displaystyle \lim_{ n \to \infty } r^n=0\)となるのは説明しなくても理解できると思います。

一方で\(r≦-1\)の場合、\(\displaystyle \lim_{ n \to \infty } r^n\)は振動します。\(r<-1\)では値が無限大に大きくなるものの、正の無限大と負の無限大が交互に現れるため、この場合は極限が存在しないと考えます。

無限等比数列の極限を計算する

それでは、実際に無限等比数列の極限に関する問題を解いてみましょう。以下の式の極限は何でしょうか。

\(5^n-2^n\)

以下のように計算しましょう。

\(\displaystyle \lim_{ n \to \infty } (5^n-2^n)\)

\(=\displaystyle \lim_{ n \to \infty } 5^n\left\{1-\left(\displaystyle\frac{2}{5}\right)^n\right\}\)

\(=∞(1-0)\)

\(=∞\)

また、次の式の極限は何でしょうか。

\(\displaystyle\frac{5^{n+1}-3^n}{5^n-4^n}\)

次のように計算しましょう。

\(\displaystyle \lim_{ n \to \infty } \displaystyle\frac{5^{n+1}-3^n}{5^n-4^n}\)

\(=\displaystyle \lim_{ n \to \infty } \displaystyle\frac{5-\displaystyle\frac{3^n}{5^n}}{1-\displaystyle\frac{4^n}{5^n}}\)

\(=\displaystyle\frac{5-0}{1-0}\)

\(=5\)

このように計算することで答えを得ることができます。

無限等比数列の収束条件

それでは、先ほど解説した条件を用いて無限等比数列の収束条件を計算しましょう。以下の式について、収束するように\(x\)の範囲を求めましょう。

\(\left(\displaystyle\frac{3x}{x^2+2}\right)^n\)

収束するためには、以下の条件を満たす必要があります。

\(-1<\displaystyle\frac{3x}{x^2+2}≦1\)

\(-1<\displaystyle\frac{3x}{x^2+2}\)より、以下のように計算しましょう。

\(-1<\displaystyle\frac{3x}{x^2+2}\)

\(x^2+3x+2>0\)

\((x+2)(x+1)>0\)

\(x<-2,-1<x\) – ①

また\(\displaystyle\frac{3x}{x^2+2}≦1\)より、以下のように計算しましょう。

\(\displaystyle\frac{3x}{x^2+2}≦1\)

\(0≦x^2-3x+2\)

\(0≦(x-1)(x-2)\)

\(x≦1,2≦x\) – ②

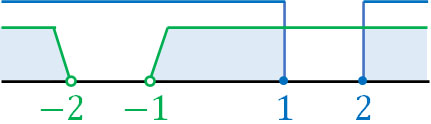
①かつ②である必要があるため、答えは\(x<-2\)、\(-1<x≦1\)、\(2≦x\)となります。条件を利用することにより、答えを得ることができます。

隣接2項間の漸化式と極限

無限等比数列の計算では、漸化式が関わる問題を解かなければいけないこともあります。漸化式と極限について、漸化式を利用して一般項を得ることができれば、容易に答えを得ることができます。

それでは、以下の問題を解いてみましょう。

\(a_1=1\)、\(a_{n+1}=3a_n+4\)となる数列\(\{a_n\}\)の極限を求めましょう。

特性方程式を利用すると、\(α=3α+4\)であるため、\(α=-2\)です。そのため、以下の式を作れます。

\(a_{n+1}-α=3(a_n-α)\)

\(a_{n+1}+2=3(a_n+2)\)

数列\(\{a_n+2\}\)は初項\(a_1+2=3\)、公比3の等比数列です。そのため、以下のように一般項を計算できます。

\(a_n+2=3^n\)

\(a_n=3^n-2\)

次に、この数列の極限を計算しましょう。

\(\displaystyle \lim_{ n \to \infty } (3^n-2)\)

\(=∞\)

こうして、答えを得ることができました。漸化式と極限に関する問題について、漸化式を利用して一般項を計算すれば、容易に答えを得られます。

はさみうちの原理を利用する漸化式と極限

なお場合によっては、極限で学ぶ内容を利用して漸化式に関する問題を解かなければいけないことがあります。以下の問題を解いてみましょう。

\(a_1=1\)、\(a_{n+1}=\displaystyle\frac{1}{2}\left(a_n+\displaystyle\frac{1}{25a_n}\right)\)となる数列\(\{a_n\}\)があります。

\(a_n>\displaystyle\frac{1}{5}\)を証明しましょう。
\(a_{n+1}-\displaystyle\frac{1}{5}<\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)を証明しましょう。
\(\displaystyle \lim_{ n \to \infty } a_n\)を求めましょう。

数列\(\{a_n\}\)の一般項を計算するのは難しいため、ほかの方法によって漸化式の極限を計算しましょう。

1) \(a_n>\displaystyle\frac{1}{5}\)を証明しましょう

漸化式が関わる証明では数学的帰納法を利用するとうまくいくことが多いです。そこで、以下のように証明しましょう。

・[1] \(n=1\)のときに成り立つと証明する

\(n=1\)のとき、\(a_1=1\)であるため、\(a_1>\displaystyle\frac{1}{5}\)です。

・[2] \(n=k\)のときに成り立つと仮定し、\(n=k+1\)であっても成り立つことを証明する

\(n=k\)のとき、\(a_k>\displaystyle\frac{1}{5}\)が成り立つと仮定します。なお\(n=k+1\)のとき、つまり\(a_{k+1}>\displaystyle\frac{1}{5}\)が成り立つと証明すればいいです。言い換えると、\(a_{k+1}-\displaystyle\frac{1}{5}>0\)を証明しましょう。

そこで、\(a_{k+1}=\displaystyle\frac{1}{2}\left(a_k+\displaystyle\frac{1}{25a_k}\right)\)を利用して以下のように変形しましょう。

\(a_{k+1}=\displaystyle\frac{1}{2}\left(a_k+\displaystyle\frac{1}{25a_k}\right)\)

\(a_{k+1}-\displaystyle\frac{1}{5}=\displaystyle\frac{1}{2}\left(a_k+\displaystyle\frac{1}{25a_k}\right)-\displaystyle\frac{1}{5}\)

\(a_{k+1}-\displaystyle\frac{1}{5}=\displaystyle\frac{1}{50a_k}(25a_k^2+1-10a_k)\)

\(a_{k+1}-\displaystyle\frac{1}{5}=\displaystyle\frac{1}{50a_k}(5a_k-1)^2\)

\(a_k>\displaystyle\frac{1}{5}\)であるため、\(a_{k+1}-\displaystyle\frac{1}{5}>0\)です。つまり、\(a_{k+1}>\displaystyle\frac{1}{5}\)となります。[1]と[2]より、すべての自然数\(n\)で\(a_n>\displaystyle\frac{1}{5}\)になると証明できました。

2) \(a_{n+1}-\displaystyle\frac{1}{5}<\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)を証明しましょう。

右辺から左辺を引きましょう。

\(\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)-a_{n+1}+\displaystyle\frac{1}{5}\)

\(=\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)\(-\displaystyle\frac{1}{2}\left(a_n+\displaystyle\frac{1}{25a_n}\right)\)\(+\displaystyle\frac{1}{5}\)

\(=\displaystyle\frac{1}{10}-\displaystyle\frac{1}{50a_n}\)

\(a_n>\displaystyle\frac{1}{5}\)であるため、\(\displaystyle\frac{1}{10}-\displaystyle\frac{1}{50a_n}>0\)です。こうして、\(a_{n+1}-\displaystyle\frac{1}{5}<\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)を証明できました。

3) \(\displaystyle \lim_{ n \to \infty } a_n\)を求めましょう

問題1と問題2より、以下の関係が成り立ちます。

\(0<a_{n+1}-\displaystyle\frac{1}{5}<\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)

そこで、\(a_{n+1}-\displaystyle\frac{1}{5}<\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)について、不等号を等号に変えて漸化式の一般項を計算しましょう。

\(a_{n+1}-\displaystyle\frac{1}{5}=\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)について、数列\(\left\{a_n-\displaystyle\frac{1}{5}\right\}\)は初項\(1-\displaystyle\frac{1}{5}=\displaystyle\frac{4}{5}\)、公比\(\displaystyle\frac{1}{2}\)の等比数列です。そのため、以下の式を作れます。

\(a_{n}-\displaystyle\frac{1}{5}=\left(\displaystyle\frac{1}{2}\right)^{n-1}·\displaystyle\frac{4}{5}\)

この計算より、\(\displaystyle\frac{1}{2}\left(a_n-\displaystyle\frac{1}{5}\right)\)\(=\left(\displaystyle\frac{1}{2}\right)^{n}·\displaystyle\frac{4}{5}\)とわかります。そこで、等号を不等号に戻すと以下のようになります。

\(a_{n}-\displaystyle\frac{1}{5}<\left(\displaystyle\frac{1}{2}\right)^{n}·\displaystyle\frac{4}{5}\)

なお\(\displaystyle \lim_{ n \to \infty } \left(\displaystyle\frac{1}{2}\right)^{n}·\displaystyle\frac{4}{5}=0\)であるため、はさみうちの原理より、\(\displaystyle \lim_{ n \to \infty } \left(a_{n}-\displaystyle\frac{1}{5}\right)=0\)となります。つまり、\(\displaystyle \lim_{ n \to \infty } a_n=\displaystyle\frac{1}{5}\)です。

こうして、式の変換とはさみうちの原理を利用することにより、一般項を計算することなく答えを得ることができました。