数学で統計学を学ぶとき、二項分布を学びます。確率の計算では、「反復試行の確率」の計算をすることがあります。反復試行の確率を利用してデータにすると二項分布となります。
二項分布は多くの場面で利用され、二択のときに活用されます。二択となるケースは多く、二項分布を利用することによって平均値(期待値)や分散、標準偏差を計算できます。
統計学で二項分布が頻繁に利用されるのは、正規分布に近似できるからです。複雑な計算であっても、二項分布の場合は公式によって簡単に期待値や分散を計算できるのです。
統計学ですべての人が二項分布を学びます。そこで正規分布を利用し、どのように平均(期待値)や分散まで計算すればいいのか解説していきます。
もくじ
二択のとき、二項分布が役に立つ
まず、二項分布とは何なのでしょうか。二択となる場合、二項分布を利用できると考えましょう。世の中には、二択となるケースが非常にたくさんあります。
例えばコインを投げるとき、表または裏の二択です。サイコロを投げるとき、1の目を基準にするのであれば、1の目とそれ以外となります。このように考えると、二択となる場面は非常に多いと理解できます。
- 薬が効くか効かないか
- テレビを見るか見ないか
- 週に2時間以上、運動をするかしないか
このようなとき、二項分布を利用できるというわけです。ほとんどの事象は二択であるため、統計学では二項分布が頻繁に利用されるというわけです。このとき重要なのは、二項分布を正規分布と同様に扱えることです。
例えばコインを10回投げるとき、表になる回数はいくらになるでしょうか。このとき、すべて表が出たり、すべて裏が出たりする確率は非常に低いと予想できます。一方で表が5回、裏が5回となる確率は高いと予想できます。
そのため表が出る回数をグラフにすると、以下のようなグラフを描くことができます。
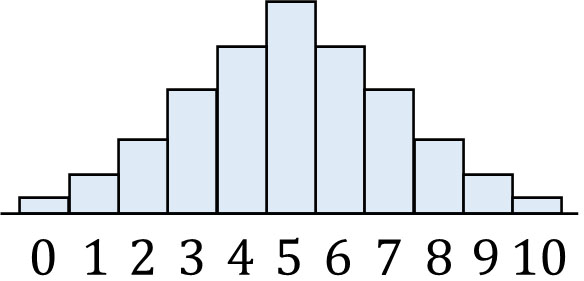
このように二項分布を描くと、正規分布と同じであるとわかります。つまり二項分布というのは、正規分布とみなして計算できるのです。
二項分布で重要となる反復試行の確率の計算
それでは、どのように二項分布を計算すればいいのでしょうか。二項分布を理解するためには、反復試行の確率を復習しなければいけません。同じことを繰り返すのが反復試行の確率と理解しましょう。
例えば以下の問題の答えは何でしょうか。
- サイコロを5回投げるとき、1の目が2回出る確率はいくらでしょうか。
サイコロを投げて1が出る確率は\(\displaystyle\frac{1}{6}\)です。また、1以外の目が出る確率は\(\displaystyle\frac{5}{6}\)です。1の目が2回出る必要があるため、以下の計算式を作ります。
\(\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^3\)
また5回サイコロを投げて、その中から2ヵ所について1の場所を選ぶことになります。
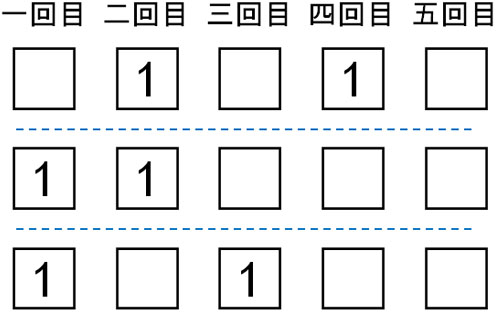
そこで組み合わせを利用し、以下の式を作りましょう。
\(_5C_2\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^3=\displaystyle\frac{625}{3888}\)
こうして、「組み合わせ(C)」「1が出る確率」「1が出ない確率」の3つを利用することによって、1の目が2回出る確率を計算することができました。
それでは、サイコロを100回投げるとき、1の目が\(k\)回出る確率はいくらになるでしょうか。先ほどの計算式を少し変えると、以下のようになります。
\(_{100}C_k\left(\displaystyle\frac{1}{6}\right)^k\left(\displaystyle\frac{5}{6}\right)^{100-k}\)
次に、サイコロを投げる場面ではなく、製品を作る場面を考えてみましょう。例えば、以下の問題の答えは何でしょうか。
- \(\displaystyle\frac{1}{100}\)の確率で不良品が出る場合、300個を調べて5個の不良品が出る確率はいくらになるでしょうか。
この場合、式は以下のようになります。
\(_{300}C_5\left(\displaystyle\frac{1}{100}\right)^5\left(\displaystyle\frac{99}{100}\right)^{95}\)
このようにして、反復試行の確率を計算します。
中心極限定理により、二項分布は正規分布へ近似できる
また反復試行の確率の計算について、すべてのパターンを計算してグラフを描くと、二項分布となります。例えばサイコロを600回投げ、1の目が出る回数が最も多いケースは100回であると容易に予想できます。そのため、1の目が出る確率は以下のようなグラフになります。
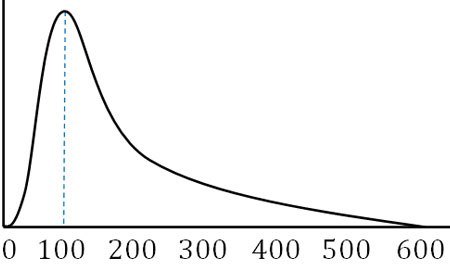
当然ながら、ピッタリ100回になるケースは稀です。1が99回出ることがあれば、1が101回出ることもあります。ただ全体の確率では、1が100回出る確率が高いというわけです。
また100を基準にして、数字が大きくなるほど(または小さくなるほど)、確率は減少していきます。例えば、1が600回出る確率はほぼゼロであることは容易に理解できます。こうしてグラフを描くと、正規分布へ近似できるというわけです。
二項分布というのは、「試行回数が多いと必ず正規分布とみなすことができる」という性質があります。この性質を統計学では中心極限定理といいます。
「何度も繰り返し測定する場合、値の合計値(または平均値)は必ず正規分布になる」という性質が中心極限定理です。二項分布においては、中心極限定理によって「どのような二項分布であっても正規分布と捉えることができる」と理解しましょう。
公式を利用し、平均(期待値)や分散、標準偏差を計算する
正規分布へ近似できるということは、二項分布を正規分布と考え、平均(期待値)や分散、標準偏差を計算できることを意味します。そこで正規分布の性質を利用し、期待値や分散を計算しましょう。
なお正規分布で期待値や分散、標準偏差を計算する場合、通常は少し複雑な計算をしなければいけません。一方で二項分布の場合、平均(期待値)や分散を出す非常に簡単な公式があります。
まずデータ数(試行回数)が\(n\)回、確率が\(p\)の場合、二項分布の場合は以下の公式を利用することによって平均(期待値)を計算できます。

例えばサイコロを60回投げ、1の目が出る期待値(1が出る回数の合計)は何でしょうか。1の目が出る確率は\(\displaystyle\frac{1}{6}\)であるため、期待値は以下になります。
\(60×\displaystyle\frac{1}{6}=10\)
それでは、分散はどのように計算すればいいのでしょうか。二項分布で分散を計算する場合、以下の公式を利用できます。
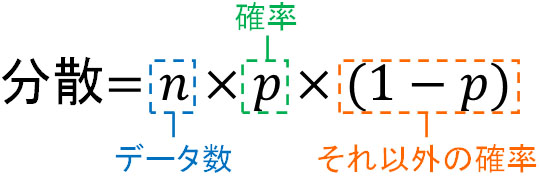
例えばサイコロを60回投げ、1の目が出るときの分散は何でしょうか。1以外の目が出る確率は\(\displaystyle\frac{5}{6}\)です。そのため、以下の式を作ることができます。
\(60×\displaystyle\frac{1}{6}×\displaystyle\frac{5}{6}=\displaystyle\frac{25}{3}\)
また標準偏差は分散の平方根によって計算するため、以下のようになります。
\(\sqrt{\displaystyle\frac{25}{3}}=\displaystyle\frac{5\sqrt{3}}{3}\)
こうして平均(期待値)だけでなく、分散と標準偏差を出すことができました。
二項分布と標準正規分布を利用し、確率の計算を行う
それでは二項分布について、実際に正規分布を利用することで確率を計算してみましょう。
- サイコロを720回投げ、1の目が135回出る確率はいくらでしょうか。
以下の計算式を作ることによって、確率を得ることができます。
\(_{720}C_{135}\left(\displaystyle\frac{1}{6}\right)^{135}\left(\displaystyle\frac{5}{6}\right)^{585}\)
ただ、この計算をするのは大変です。そこで平均値\(μ\)や分散、標準偏差\(σ\)を計算しましょう。以下のようになります。
- 平均(期待値):\(720×\displaystyle\frac{1}{6}=120\)
- 分散:\(720×\displaystyle\frac{1}{6}×\displaystyle\frac{5}{6}=100\)
- 標準偏差:\(\sqrt{100}=10\)
次に標準正規分布へ変換しましょう。「標準正規分布を利用することによって確率を出す方法」を理解している場合、以下の公式を利用することによって確率変数\(Z\)を計算しましょう。
\(Z=\displaystyle\frac{X-μ}{σ}\)
\(=\displaystyle\frac{135-120}{10}\)
\(=1.5\)
こうして、標準正規分布での確率変数\(Z\)は1.50であるとわかりました。そこで、標準正規分布表で1.50となる部分を確認しましょう。

こうして、確率変数\(Z\)が1.50となる確率は0.06681(約6.68%)であるとわかります。そのためサイコロを720回投げ、1の目が135回出る確率は6.68%です。
二項分布を正規分布とみなし、標準正規分布表を利用することによって、特定の事象が起こる確率を計算することができます。そこで期待値や分散、標準偏差を利用し、確率を計算できるようにしましょう。
二項分布と正規分布の性質を理解し、確率を計算する
多くの場面で二択が利用されます。二択の場合、二項分布となります。このとき反復試行の確率を計算することによって、確率を得ることができます。
また二項分布となる場合、中心極限定理により、試行回数が多いと必ず正規分布とみなせるようになります。そこで正規分布へ近似することによって、平均(期待値)や分散、標準偏差を計算できるようになりましょう。
正規分布について、期待値と標準偏差を利用することによって確率を計算できます。標準正規分布を利用して確率を求めるのです。
数学で統計学を学ぶとき、二項分布は必ず学ぶ内容の一つです。そこで二項分布の性質や確率の計算方法を理解しましょう。






