確率の計算をするとき、確率変数について期待値や分散、標準偏差を計算することがあります。つまり一つの事象について、予想可能な得られる値やばらつきを求めるのです。
ただ場合によっては、2つの事象を足すことによって、2つ以上のデータを一つにすることがあります。またかけ算によって、データを変えることもあります。つまり、和や積によって確率変数の変換をするのです。その場合、期待値や分散、標準偏差がどのように変化するのか理解しなければいけません。
またデータを変換するとき、それぞれのデータが独立かどうかを確かめましょう。独立であれば、データの足し算や掛け算によって新たな期待値や分散、標準偏差の計算が容易になります。
統計学では期待値や分散、標準偏差の計算をします。そこで、2つのデータを組み合わせるときに期待値や分散、標準偏差がどのように変化するのか学びましょう。
もくじ
確率変数の期待値・分散・標準偏差に数字を加える
確率変数の期待値\(E(X)\)とは、一つのデータに関する平均値を意味します。また一つのデータについて、ばらつきを表すのが分散と標準偏差です。
そこで確率変数の変換を学ぶ前に、サイコロを例にして期待値や分散、標準偏差を計算してみましょう。例えばサイコロを投げるとき、出る目としては1~6の6種類があります。

また、それぞれの数字について出る確率はすべて\(\displaystyle\frac{1}{6}\)です。そのため確率分布より、期待値\(E(X)\)を計算すると以下のようになります。
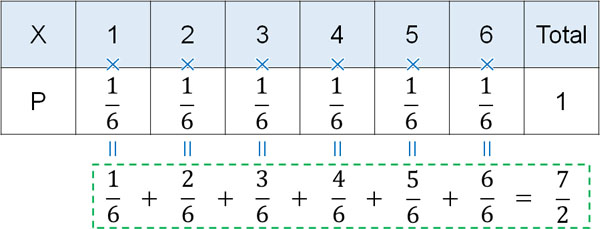
一回のサイコロを投げる場合、3.5\(\left(\displaystyle\frac{7}{3}\right)\)を得られることを期待できます。もちろんサイコロに3.5はないものの、何回も投げて平均化すると3.5になるというわけです。期待値というのは、平均値でもあります。
また詳細な説明は省きますが、期待値を利用することで分散\(V(X)\)と標準偏差\(σ(X)\)を以下のように計算できます。
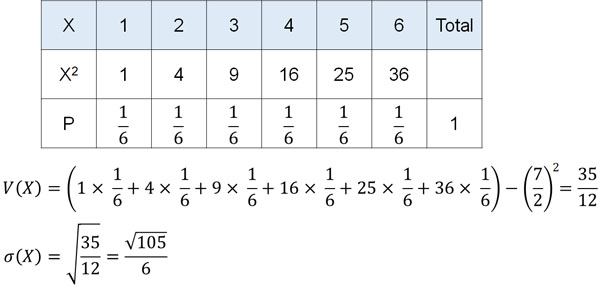
分散\(V(X)\)と標準偏差\(σ(X)\)はばらつきを表しています。ちなみに、\(\displaystyle\frac{\sqrt{105}}{6}≒1.7\)です。ばらつきを得ることによって、どれだけ期待値(平均値)からずれる可能性があるのか把握できます。
和や積による期待値、分散、標準偏差の変化
こうしたデータに対して、確率変数の変換では値を加えます。データの形を変えたり、ほかのデータを加えたりすることがあるため、足し算やかけ算によって期待値や分散、標準偏差がどのように変化するのか理解しなければいけません。
先に結論を述べると、足し算やかけ算によって以下のように変化します。
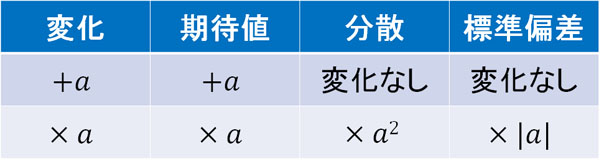
なぜ、このように変化するのか理由を理解しましょう。理由を学べば、公式を暗記しなくても確率変数の変換を行えるようになります。
足し算(和)による確率変数の変化
まず、足し算について考えてみましょう。期待値というのは前述の通り平均値と意味が同じです。そのためすべての確率変数に対して同じ値を足す場合、それに応じて期待値(平均値)は増加します。
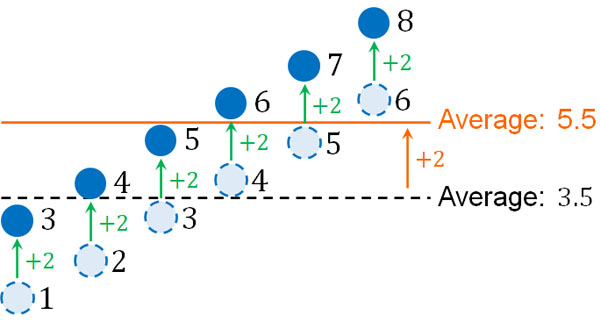
例えばサイコロの出る目の期待値は先ほど計算した通り\(\displaystyle\frac{7}{2}=3.5\)です。そこですべての確率変数に2を加える場合、新たな期待値(新たな平均値)は5.5になります。
以下のようにすべてのデータが等しく\(+2\)になるため、当然ながら期待値(平均値)も2増えるというわけです。
一方で分散と標準偏差は変わりません。理由としては、ばらつきは変化しないからです。
分散と標準偏差はばらつきを表しており、「期待値(平均値)からどれだけズレているのか」を意味します。確率変数に対して同じ数を足すことになるため、期待値は変化するものの、期待値からのズレは同じです。これが、確率変数の和で分散や標準偏差が変化しない理由です。
かけ算(積)による確率変数の変化
次にかけ算によって確率変数がどのように変化するのか確認しましょう。かけ算をする場合、確率変数はその分だけ大きく移動することになります。
例として、サイコロの確率変数に対して2をかけてみましょう。以下のようになります。
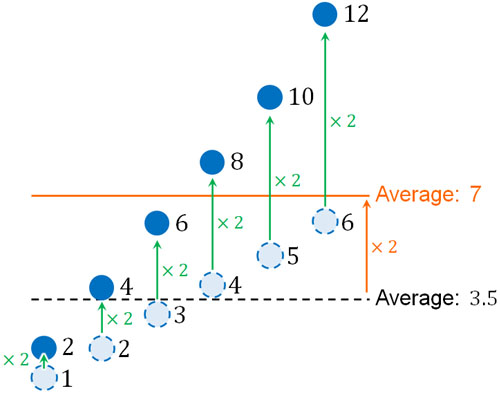
すべての値について2倍するため、期待値(平均値)も2倍になります。これが、「かけ算をするとき、確率変数の期待値もかけ算によって計算できる理由」です。
またかけ算をする場合、ばらつきが変動します。分散の計算では、「平均値との差」を二乗することで計算します。そのためかけ算をする場合、分散は二乗に比例します。
一方で分散の平方根を利用することによって標準偏差を計算できます。二乗した後に平方根を利用するため、必ず正の値になります。そのため確率変数を\(a\)倍する場合、標準偏差は\(|a|\)倍となります。
確率変数の変換を行う
先ほど、サイコロを一回投げることによる期待値\(E(X)\)は3.5、分散\(V(X)\)は\(\displaystyle\frac{35}{12}\)、標準偏差\(σ(X)\)は\(\displaystyle\frac{\sqrt{105}}{6}≒1.7\)と計算しました。
それでは確率変数\(X\)に対して、\(Z=2X+3\)で表される確率変数\(Z\)の期待値や分散、標準偏差は何でしょうか。
・期待値\(E(Z)\)
\(Z=2X+3\)であるため、期待値を2倍したあと、3を足しましょう。以下のようになります。
\(E(Z)=2×3.5+3=10\)
・分散\(V(Z)\)
かけ算に対して二乗すればいいため、分散は以下のようになります。
\(V(Z)=2^2×\displaystyle\frac{35}{12}=\displaystyle\frac{35}{3}\)
・標準偏差\(σ(Z)\)
絶対値のかけ算をすればいいため、標準偏差は以下のようになります。
\(σ(Z)=2×\displaystyle\frac{\sqrt{105}}{6}=\displaystyle\frac{\sqrt{105}}{3}\)
このようにして足し算とかけ算を利用することによって、確率変数の変換をするときの期待値や分散、標準偏差を計算できます。
確率変数の独立と従属の意味
ここまでの内容を理解した後、確率変数の独立と従属を学びましょう。確率変数の変換では、足し算やかけ算をすることによって値の変化を知ることだけでなく、2つの要素を組み合わせることも重要になります。
2つの要素(確率変数)を組み合わせるためには、2つの要素が独立であるかどうかを事前に確認する必要があります。ちなみに2つの要素に関係性がない場合、従属関係となります。
それでは、どのようにして独立と従属を見分ければいいのでしょうか。独立かどうかを確認するとき、事象Aと事象Bについて、以下を満たすかどうかを確認しましょう。
- \(P(A∩B)=P(A)×P(B)\)
これを満たす場合、2つの事象は独立です。一方でこの条件を満たさない場合、2つの事象は従属です。例えば、以下の事象を考えてみましょう。
- 事象A:サイコロを投げて3以上になる確率
- 事象B:サイコロを投げて2の倍数になる確率
事象Aについて、サイコロを投げて3以上になる確率は\(P(A)=\displaystyle\frac{2}{3}\)です。事象Bについて、サイコロを投げて2の倍数になる確率は\(P(B)=\displaystyle\frac{1}{2}\)です。
また「サイコロを投げて3以上になり、かつ2の倍数となるサイコロの目」は4と6です。そのため、事象Aと事象Bを同時に満たす確率\(P(A∩B)\)は\(\displaystyle\frac{1}{3}\)です。\(P(A∩B)=P(A)×P(B)\)が成り立つため、事象Aと事象Bは独立です。
一方、以下の場合はどうでしょうか。
- 事象A:サイコロを投げて3以上になる確率
- 事象B:サイコロを投げて3の倍数になる確率
事象Aについて、サイコロを投げて3以上になる確率は\(P(A)=\displaystyle\frac{2}{3}\)です。事象Bについて、サイコロを投げて3の倍数になる確率は\(P(B)=\displaystyle\frac{1}{3}\)です。
また「サイコロを投げて3以上になり、かつ3の倍数となるサイコロの目」は3と6です。そのため、事象Aと事象Bを同時に満たす確率\(P(A∩B)\)は\(\displaystyle\frac{1}{3}\)です。
\(P(A)×P(B)=\displaystyle\frac{2}{3}×\displaystyle\frac{1}{3}=\displaystyle\frac{2}{9}\)
\(P(A∩B)=P(A)×P(B)\)が成り立たないため、事象Aと事象Bは従属です。
確率に影響を与えない場合、確率変数は独立となる
2つの事象について、独立なのか従属なのか見分けるのは難しいです。先ほどの例を確認すれば、この理由がわかるはずです。そこで、独立かどうかの確認をする必要があるというわけです。
それでは確率変数での独立と従属にはどのような意味があるのでしょうか。確率変数の独立とは、2つの事象について、「一方の事象が発生する場合であっても、もう一方の事象の確率に影響を与えない」ことを意味します。つまり、一つの事象が発生しても確率が変化しない場合は独立というわけです。
数学では、「事象Bが起こるとき、同時にAが起こる確率」を\(P(A|B)\)と表します。事象が独立の場合、確率Bが起こっても事象Aの確率\(P(A)\)に影響を与えないため、以下のようになります。
- \(P(A|B)=P(A)\)
同様に、事象Aと事象Bが独立の場合、以下も成り立ちます。
- \(P(B|A)=P(B)\)
「事象Aが起こるととき、同時にBも起こる確率」を\(P(B|A)\)と表すことができます。独立の場合、事象Aは事象Bの確率\(P(B)\)に影響を与えないため、\(P(B|A)\)と\(P(B)\)は同じになります。
それでは独立と従属について、先ほど解説した問題を確認してみましょう。まず、以下のケースはどのように考えればいいのでしょうか。
- 事象A:サイコロを投げて3以上になる確率
- 事象B:サイコロを投げて2の倍数になる確率
前述の通り、サイコロを投げて2の倍数になる確率\(P(B)\)は\(\displaystyle\frac{1}{2}\)です。
次に「サイコロを投げて3以上のとき、同時に2の倍数にもなるケース」について考えてみましょう。3以上の数は4通りです(3,4,5,6)。また3以上の数のうち、2の倍数になるのは4と6の2通りです。そのため事象Aが発生しているとき、同時に事象Bが発生する確率\(P(B|A)\)は\(\displaystyle\frac{2}{4}=\displaystyle\frac{1}{2}\)です。
こうして\(P(B|A)=P(B)\)となるため、2つの事象は独立となります。一方で以下のケースはどうでしょうか。
- 事象A:サイコロを投げて3以上になる確率
- 事象B:サイコロを投げて3の倍数になる確率
サイコロを投げて3の倍数になる確率\(P(B)\)は\(\displaystyle\frac{1}{3}\)です。それでは、「サイコロを投げて3以上のとき、同時に3の倍数になる確率\(P(B|A)\)」はいくらでしょうか。
サイコロを投げて3以上のケースは4通りです。また3以上であり、3の倍数になるケースは3と6の2通りです。そのため、\(P(B|A)=\displaystyle\frac{2}{4}=\displaystyle\frac{1}{2}\)です。\(P(B|A)\)と\(P(B)\)が一致しないため、事象Aと事象Bは従属関係です。
独立な場合の期待値の計算
なぜ独立と従属を学ぶ必要があるかというと、2つの事象を組み合わせるとき、独立であるかどうかが重要になるからです。
まず、2つの事象を足す場合については、独立であるかどうかを確認する必要がありません。例えば「確率変数\(X\)の期待値\(E(X)\)」と「確率変数\(Y\)の期待値\(E(Y)\)」について、以下のように期待値を足すことによって計算できます。
- \(E(X+Y)=E(X)+E(Y)\)
期待値というのは、平均値という一つの値です。そのため独立かどうかに関係なく、2つの事象を足すときは足し算をすればいいです。また\(a\)と\(b\)を定数とするとき、以下の公式も成り立ちます。
- \(E(aX+bY)=aE(X)+bE(Y)\)
ここまでの内容については、特に問題ないと思います。期待値(平均値)を足したり、期待値のかけ算をした後に足したりすることによって、2つの事象を組み合わせた期待値を得ることができます。
一方で2つの期待値をかける場合、2つの事象が独立な場合において、以下の公式が成り立ちます。
- \(E(X×Y)=E(X)×E(Y)\)
確率変数の積では、従属関係ではこの公式を利用できません。必ず独立関係である必要があります。なぜ確率変数の期待値をかけるとき、2つの事象が独立関係でなければいけないのでしょうか。
独立でないと、かけ算をしてはいけない理由
従属関係というのは、確率が互いに影響を与えることを意味します。そのため、期待値のかけ算をするといけないのです。例えば、10年に1回の頻度で壊れる機器があるとします。10年に一回壊れるため、1年を365日とすると、3650日に一回の頻度で故障します。
この機器を3つ同時に稼働させる場合、同じ日に故障する確率は以下のようになります。
\(\left(\displaystyle\frac{1}{3650}\right)^3=\displaystyle\frac{1}{48627125000}\)
つまり、数学的に同じ日に3つの機器が同時に故障することはほとんどありません。また機器を4つや5つに増やせば、同時に故障することは考えられません。独立である場合、かけ算によって計算することができます。
一方で故障の原因が「ある日の大規模地震によって巨大な津波が発生した」であればどうでしょうか。巨大津波という事象が発生するとき、一つの機器だけでなく、同時にほかの機器も100%の確率で故障します。
つまりこの場合の機器の故障というのは、機器A・機器B・機器Cが独立関係ではなく、従属関係にあるといえます。従属関係の場合、一つの事象によって確率が大きく変化します。今回の例であれば、巨大津波によって100%の確率で機器が壊れるというわけです。
こうして起こった出来事が東日本大震災によって起こった福島原発事故です。以下は当時の様子です。

出典:Air Photo Service Co. Ltd
理論上、原子力発電所での事故の発生確率はゼロのように思われていました。しかし実際には従属関係にあり、大震災による津波によって大規模な事故へと発展したのです。
こうした故障を共通原因故障(Common Cause Failure)と呼びます。原子力発電所など一回の事故によって多大な被害をもたらす場合、共通原因故障は特に考慮しなければいけない要素です。
このように考えると、従属関係の場合に期待値をかけてはいけないとわかります。一つの出来事が確率に影響を与える場合、2つの期待値をかけても正しい答えを得られないのです。また、2つの事象が独立なのか従属なのかを理解するのがなぜ重要なのかもわかります。
独立のとき、分散では二乗の計算をした後に足す
なお2つの要素を足すときについて、分散の計算方法についても理解しましょう。期待値については、独立や従属に関係なく足し算することができると説明しました。一方で分散はどうなのでしょうか。
分散については、2つの事象が独立のとき、以下の公式が成り立ちます。
- \(V(X+Y)=V(X)+V(Y)\)
つまり足し算をするとき、独立でない場合、2つの分散を足してはいけません。詳しい説明を省きますが、2つの事象に関係性がある場合(従属関係の場合)、2つの事象を足すとき、共分散を考慮することになります。共分散とは、2つの事象がどれだけ関係しているのかを表すばらつきです。
つまり2つの確率変数を足すとき、分散\(\)というのは、ザックリと以下のようになると考えましょう。
- \(V(X+Y)=\)事象Aの分散\(+\)事象Bの分散\(+\)共分散
ただ2つの確率変数が独立の場合、事象Aと事象Bに相関性はないため、共分散は0になります。そのため独立の場合、分散を足してもいいというわけです。
またそれぞれの事象(確率変数)が独立の場合、\(a\)と\(b\)を定数とすると、以下の公式を利用できます。
- \(V(aX+bY)=a^2V(X)+b^2V(Y)\)
かけ算をする場合、分散では二乗を利用します。そのため、この公式については特に問題なく理解できると思います。
確率変数の変換をするとき、事象が独立なのか従属なのかを見極めましょう。分散を計算するとき、独立であれば足し算によって計算できます。ただ独立ではない場合、共分散を考慮して分散を計算しなければいけません。
確率変数の変換と独立性を学び、期待値や分散、標準偏差を計算する
統計学で期待値や分散、標準偏差の計算をすることが頻繁にあります。また得られた期待値や分散について、足し算やかけ算をすることがあります。このとき、どのように値が変化するのか学びましょう。
なお2つの事象を足したりかけたりするとき、独立性の判定が重要になります。独立なのか、それとも従属なのかを判断できるようになりましょう。
期待値の足し算であれば、独立や従属に関係なく値を足すことによって答えを得られます。一方で確率変数のかけ算では、独立の場合のみかけ算を利用できます。また分散の足し算についても、独立のときに分散を足すようにしましょう。
確率の期待値や分散、標準偏差の計算をするとき、正しい方法があります。そこで値の変化や独立の意味を理解し、確率を計算できるようにしましょう。






