高校数学など、高度な計算では文字を使います。文字の計算では式の展開をしたり、因数分解をしたりします。
乗法公式と分配法則を理解していれば、式の展開は難しくありません。一方、因数分解は公式を理解していてもできないことが多いです。因数分解には解き方があります。問題をみると同時に解き方を思い浮かべることができれば、因数分解をすることができます。
高校数学ではたすき掛けや3次式の因数分解(または3次式の展開)をします。これに加えて、高度な因数分解の手順を学びましょう。
そこで式の展開や因数分解をするとき、どのように問題を解けばいいのか解説していきます。
もくじ
単項式と多項式:次数と係数
式の展開や因数分解を学ぶ前に、単項式と多項式、また次数と係数についておさらいしましょう。式の展開ができない場合、因数分解をすることはできません。
単項式とは、文字だけの式を指します。つまり、かけ算だけの式が単項式と理解しましょう。一方で多項式とは、たし算と引き算によって複数の単項式が存在する式を指します。
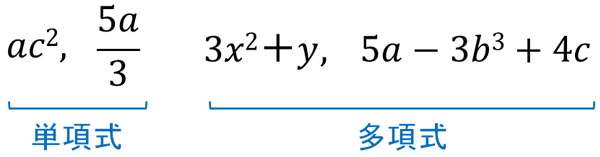
また単項式に着目するとき、項と係数、次数を理解しましょう。以下のようになります。

例えば単項式として\(3x^2\)があるとき、\(3x^2\)を項といいます。また係数は3であり、次数は2です。他には、例えば単項式として\(2a^3\)があるとき、\(2a^3\)が項です。また係数は2であり、次数は3です。
数学の問題を解くとき、これらの名前を理解しましょう。
分配法則を利用し、かっこを外せる
また式の展開や因数分解をするとき、分配法則を利用します。かっこを外すための考え方が分配法則です。以前に因数分解を学んでいる場合、分配法則については既に理解していると思います。以下のように、分配法則を利用してかっこを外すことができます。
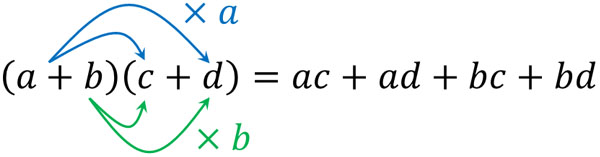
ただ高度な数学では、計算がより複雑になります。例えば、以下の式を展開するにはどうすればいいでしょうか。
- \((2x^2+x+3)(x^2+3x+4)\)
かっこの中にある単項式が多い場合であっても、分配法則によって式を展開することができます。以下のように、分配法則を利用しましょう。
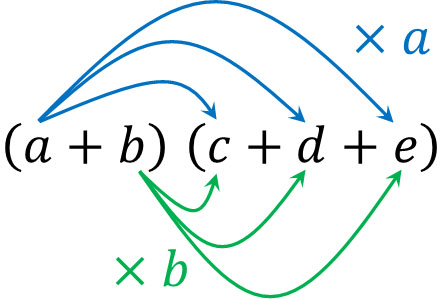
そのため分配法則を利用することによって、以下のように式を展開できます。
\((2x^2+x+3)(x^2+3x+4)\)
\(=2x^2(x^2+3x+4)+x(x^2+3x+4)\)\(+3(x^2+3x+4)\)
\(=2x^4+6x^3+8x^2+x^3+3x^2+4x\)\(+3x^2\)\(+9x\)\(+12\)
\(=2x^4+7x^3+14x^2+13x+12\)
このようにして、式の展開をすることができます。文字が同じ場合、それらを共通項といいます。そこで計算した後、共通項をまとめることによって答えを出すことができます。
因数分解で基本となる乗法公式
ここまでの内容を理解すれば、因数分解をすることができます。因数分解では乗法公式を利用します。因数分解の初歩では、以下の4つの公式を学びます。
- \((x+a)(x+b)=x^2+(a+b)x+ab\)
- \((x+a)^2=x^2+2ax+a^2\)
- \((x-a)^2=x^2-2ax+a^2\)
- \((x+a)(x-a)=x^2-a^2\)
高校数学など、高度な数学ではここに公式を追加します。一つはたすき掛けを利用して解くための公式です。もう一つが3次式の因数分解(または式の展開)をするための公式です。
それぞれについて確認していきましょう。
たすき掛けを用いる因数分解
因数分解の初歩では、2次式の係数は1です。例えば、以下のような式について因数分解をします。
- \(x^2+2x+1=(x+1)^2\)
一方、以下の式はどのように因数分解すればいいでしょうか。
- \(3x^2-4x-4\)
この場合、\(3x^2\)の係数が3です。そのため、これまでの方法では因数分解をすることができません。そこで、以下の公式を利用することになります。
- \((ax+b)(cx+d)=acx^2\)\(+(ad+bc)x\)\(+bd\)
この公式を覚える必要はありません。重要なのは、「2次式の因数分解をするとき、係数が1以外の場合、たすき掛けという方法を利用することによって因数分解する」ことです。
公式を覚えなくてもいい理由として、たすき掛けという方法を理解すれば、公式を利用しなくても因数分解することができるからです。たすき掛けでは、何の数字をかけると\(x^2\)の係数になるかを考えましょう。
例えば\(\color{red}{3x^2}-4x-4\)の場合、\(x^2\)の係数は3です。\(1×3=3\)なので、aとcの数字は1または3です。そこで、以下のように1と3の数字をたてに並べましょう。
![]()
次に、文字のない項に着目しましょう。例えば\(3x^2-4x\color{red}{-4}\)の場合、次に着目するのは-4です。一般的な因数分解であっても、文字のない項に着目することによって因数分解をします。同じように、たすき掛けについても文字のない項を確認しましょう。
そこで、どのような数字をかけると-4になるのかを考えなければいけません。2つの数字をかけることで-4になるパターンは以下の4つです。
- \(1×-4=-4\)
- \(-1×4=-4\)
- \(2×-2=-4\)
- \(-2×2=-4\)
つまり、bとdに入る数字は4パターンあります。以下のようになります。

ここまでの因数分解では、\((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)のうち、\(acx^2\)と\(bd\)に着目して答えの候補を探してきました。次に、\((ad+bc)x\)に合う数字を見つけなければいけません。そこで4つ候補のうち、\(3x^2\color{red}{-4x}-4\)になるように因数分解できる候補を選びましょう。
\((ad+bc)x\)に合う数字を見つけるため、\(a×d\)と\(b×c\)をしなければいけません。そこでたすき掛けでは、以下のように斜めにかけ算をします。
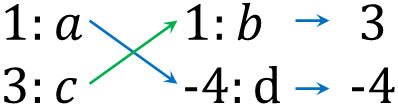
その後、\(ad\)と\(bc\)を足すことによって最適な数字を得られるかどうかを確認しましょう。今回は\(3x^2-4x-4\)の因数分解であるため、\(ad\)と\(bc\)を足して-4になる候補をみつけましょう。以下のようになります。

こうして上図のうち、右下の式を使えば\(3x^2-4x-4\)を作れることがわかります。
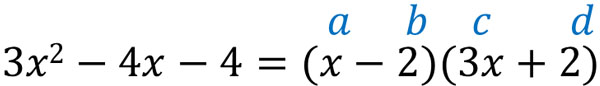
このようにして因数分解する方法がたすき掛けです。
少し複雑なたすき掛けの計算
それでは、次に少し複雑な因数分解をしてみましょう。以下の式を因数分解するにはどうすればいいでしょうか。
- \(12x^2-x-20\)
最初に着目する項は\(12x^2\)です。2つの数字をかけて12になるためには、どのような数字を利用すればいいでしょうか。以下の3つの候補があります。
- \(1×12=12\)
- \(2×6=12\)
- \(3×4=12\)
複数の候補があるため、因数分解は複雑になります。ただ、\(1×12=12\)は利用しなくてもいいと予想できます。仮にaとcが1または12の場合、たすき掛けをすると以下のように\((ad+bc)\)の数字が大きくなります。
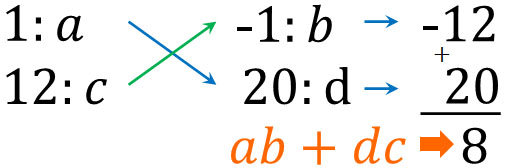
最も数字が小さくなる結果を利用したとしても、\((ad+bc)=-1\)となる結果を見つけることはできません。そこで、\(1×12=12\)は無視しましょう。
参考までに、反対に\((ad+bc)=118\)のように、\(ad\)と\(bc\)を足して答えが大きくなる場合、\(1×12=12\)を利用しなければいけない可能性が高くなります。いずれにしても、このように答えを予測してたすき掛けの答えを探していきます。
ほかには、\(2×6=12\)を含む式も答えではありません。理由としては、\(x\)の係数が-1(\(-x\))だからです。\((ad+bc)=-1\)にする必要があります。ただ\(a\)と\(c\)の両方とも偶数の場合、\((ad+bc)\)の答えは偶数になります。
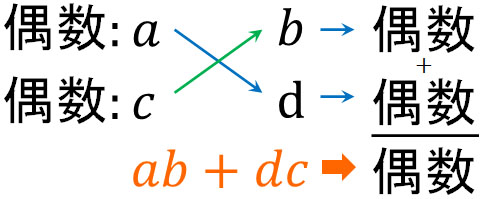
そこで、\(2×6=12\)を除外します。次に、\(12x^2-x-20\)で着目する数字は-20です。かけて-20になる数字についても複数あります。
- \(1×-20=-20\)
- \(-1×20=-20\)
- \(2×-10=-20\)
- \(-2×10=-20\)
- \(4×-5=-20\)
- \(-4×5=-20\)
ただ、このうち\(1×-20=-20\)など、大きい数字を含む式は答えではないと予測できます。理由としては先ほどと同じように、\((ad+bc)=-1\)となる必要があるため、大きい数字を利用すると答えを得ることができないからです。
また\(2×-10=-20\)を含む式も答えではありません。理由としては、\((ad+bc)\)の答えが奇数だからです。\(b\)と\(d\)の両方とも偶数だと、\((ad+bc)\)は必ず偶数になります。このように、候補が多い場合は「どのような答えになればいいのか」を予測して候補をしぼっていきましょう。
複雑な式の因数分解では、たすき掛けを利用するときに答えの予想をしましょう。答えとなる候補がいくつもあるため、すべてについてたすき掛けをしていると多くの時間を取られてしまいます。そこで、答えを予測することで計算時間を短くしなければいけません。
ここまでの内容をまとめると、aとcで利用する数字としては\(3×4=12\)です。またbとdで利用する数字は\(4×-5=-20\)または\(-4×5=-20\)です。これらの候補のうち、どれが最適なのかを一瞬で見分けるのは無理です。そこで数字を代入し、たすき掛けを利用して答えを探しましょう。
そうすると、以下の答えをみつけることができます。
- \(12x^2-x-20=(3x-4)(4x+5)\)
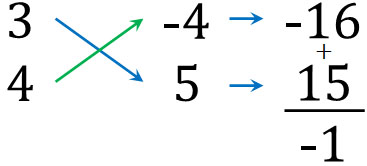
なおこの因数分解をするとき、多くの人は\(4×-5=-20\)と\(-4×5=-20\)のうち、どちらを答えにすればいいのか迷います。
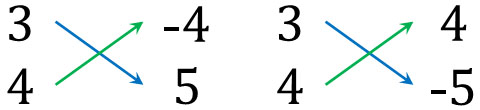
そこで、どちらの計算が\((ad+bc)=-1\)を満たすのか確認しましょう。そうすると、正しい答えを出せるようになります。
公式を利用する3次式の因数分解
次に3次式の因数分解ができるようにしましょう。先ほど、たすき掛けの公式を覚える必要はないと解説しました。公式ではなく、たすき掛けの方法を理解すればいいからです。一方、3次式の因数分解については、公式を覚えていなければ解くことができません。
そこで、以下の公式を覚えるようにしましょう。
- \(a^3+b^3=(a+b)(a^2-ab+b^2)\)
- \(a^3-b^3=(a-b)(a^2+ab+b^2)\)
- \(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
- \(a^3-3a^2b+3ab^2-b^3=(a-b)^3\)
※3次式の公式は数Ⅱの内容であるものの、問題を解けるかどうかは「公式を覚えているかどうか」だけなので、ここで覚えてしまいましょう。
公式を理解していれば、3次式の因数分解をすることができます。例えば、以下の式の因数分解をしてみましょう。
- \(27x^3-8\)
この式は以下のように変形できます。
- \(27x^3-8=(3x)^3-2^3\)
そのため、以下のように因数分解できます。
- \(27x^3-8=(3x-2)(9x^2+6x+4)\)
因数分解を行う手順
ここまでの内容は因数分解をするときの基本的な知識になります。ただ多くの場合、基礎知識だけで因数分解ができるようになることはありません。そこで、高度な因数分解をするための手順を理解しましょう。
因数分解の問題を解くとき、以下によって計算できないか考えるといいです。
- 共通因数を探す
- 文字が多い場合、最低次数に着目して整理する
- 複雑な式に対して置き換えをする
- さらに因数分解できないか確認する
- 因数分解できない場合、平方の差を利用する
それぞれの方法を確認していきましょう。
共通因数を探す
因数分解で最も基本的な解き方が共通因数を探すことです。同じ因数を見つけた後、因数分解をしましょう。例えば、以下の式はどのように因数分解すればいいでしょうか。
- \((a-b)^2+ac-bc\)
式を変形すると以下のようになります。
\((a-b)^2+ac-bc=(a-b)^2+(a-b)c\)
こうして、\((a-b)\)が共通項であるとわかります。そのため、以下のように因数分解できます。
\((a-b)^2+ac-bc\)
\(=(a-b)^2+(a-b)c\)
\(=(a-b)(a-b+c)\)
文字が多い場合、最も次数の低い文字に着目して整理する
ただ式によっては、多くの文字を含むことがあります。その場合、どのように共通因子を見つければいいのかわかりません。例えば、以下の式の因数分解はどうすればいいのでしょうか。
- \(b^2+ab+b-a-2\)
この場合、最も次数の低い文字に着目しましょう。先ほどの式では、次数の低い文字は\(a\)です。式の中に\(b^2\)が含まれているものの、\(a^2\)はありません。そこで、\(a\)に着目して式を整理しましょう。以下のようになります。
\(b^2+ab+b-a-2\)\(=a(b-1)+b^2+b-2\)
こうすれば、共通因数を見つけることで因数分解できるようになります。
\(b^2+ab+b-a-2\)
\(=a(b-1)+b^2+b-2\)
\(=a(b-1)+(b-1)(b+2)\)
\(=(b-1)(a+b+2)\)
・次数が同じ場合の因数分解
一方、次数が同じ場合はどのように因数分解すればいいのでしょうか。この場合、一つの文字に着目して式を整理するといいです。例として以下の式を因数分解しましょう。
- \(a^2(b-c)+b^2(c-a)+c^2(a-b)\)
この式では、すべての文字について最高次数の数字が同じです。そこで、一つの文字に着目しましょう。着目する文字は\(a\)でもいいし、\(b\)でもいいです。\(c\)を利用しても問題ありません。ここでは、\(a\)に着目して式を整理してみましょう。
方法としては式を展開した後、\(a\)に着目して式を整理します。その後、因数分解しましょう。
\(a^2(b-c)+b^2(c-a)+c^2(a-b)\)
\(=(b-c)a^2+b^2c-b^2a+c^2a-c^2b\)
\(=(b-c)\color{red}{a^2}-(b^2-c^2)\color{red}{a}+b^2c-c^2b\)
\(=\color{red}{(b-c)}a^2-(b+c)\color{red}{(b-c)}a+\color{red}{(b-c)}bc\)
\(=(b-c)\{a^2-(b+c)a+bc\}\)
\(=(b-c)(a-c)(a-b)\)
複雑な式に対して置き換えをする
複雑な式について、因数分解をしなければいけないことがあります。その場合、数式の置きかえをしましょう。数式を一つの文字に置きかえることによって、計算が簡単になります。具体的には、共通する式や複雑な式についてはAやXなどの文字に置きかえるといいです。
例として、以下の式を因数分解しましょう。
- \((a^2+a+1)(a^2+a+2)-12\)
式を確認すると、\(a^2+a\)が共通しています。そこで、\(a^2+a=A\)としましょう。そうすると、以下のようになります。
\((a^2+a+1)(a^2+a+2)-12\)\(=(A+1)\)\((A+2)-12\)
このように式の置きかえをすると、計算が簡単になります。以下のように因数分解しましょう。
\((a^2+a+1)(a^2+a+2)-12\)
\(=(A+1)(A+2)-12\)
\(=A^2+3A+2-12\)
\(=A^2+3A-10\)
\(=(A-2)(A+5)\)
なお、\(A=a^2+a\)です。そのため、以下のように式を変えましょう。
\((A-2)(A+5)\)
\(=(a^2+a-2)(a^2+a+5)\)
さらに因数分解できないか確認する
なお因数分解をしたあと、さらに因数分解できないか確認するようにしましょう。例えば先ほどの問題では、\(A=a^2+a\)と置き換えることによって、\((a^2+a+1)(a^2+1+2)-12\)を以下のように因数分解しました。
- \((a^2+a-2)(a^2+a+5)\)
しかし、この答えは誤りです。理由としては、さらに因数分解することができるからです。そこで、以下のように因数分解しましょう。
\((a^2+a-2)(a^2+a+5)\)
\(=(a-1)(a+2)(a^2+a+5)\)
ここまで因数分解することによって、答えを出すことができます。
因数分解できない場合、平方の差を利用する
場合によっては、問題文にある項を利用するだけでは因数分解できないことがあります。その場合、平方の差を利用しましょう。因数分解によってかっこをもつ二乗の式を作った後、引き算の式を作るのです。例えば、以下の式は意味が同じです。
- \(a^2+b^2\)
- \((a+b)^2-2ab\)
\((a+b)^2=a^2+2ab+b^2\)です。そのため、\(-2ab\)によって式は\(a^2+b^2\)になります。この性質を利用し、二乗の式を作った後に引き算を利用することによって因数分解が可能になるケースがあります。
例として、以下の式を因数分解しましょう。
- \(x^4+2x^2+9\)
\(x^2=X\)と置き換えをしたとしても、因数分解することはできません。そこで\(x^2=X\)にした後、平方の差を利用しましょう。以下のように因数分解します。
\(x^4+2x^2+9\)
\(=X^2+2X+9\)
\(=(X+3)^2-4X\)
\(=(x^2+3)^2-4x^2\)
次に\((x^2+3)=A\)、\(2x=B\)としてみましょう。すると、次のように因数分解できます。
\((x^2+3)^2-4x^2\)
\((x^2+3)^2-(2x)^2\)
\(=A^2-B^2\)
\(=(A+B)(A-B)\)
\(=(x^2+3+2x)(x^2+3-2x)\)
式の展開と因数分解には手順がある
分配法則と乗法公式を覚えていれば、式の展開をすることができます。また式の展開ができれば、因数分解ができるようになります。因数分解は式の展開よりも複雑であり、たすき掛けの方法や3次式の因数分解の公式を覚えるようにしましょう。
ただ因数分解では、たすき掛けや3次式の公式を覚えたとしても計算できないことが多いです。そこで、因数分解の解き方を学びましょう。
因数分解で最も一般的な方法として、共通因数を探すやり方があります。それに加えて、次数の低い文字に着目したり、文字の置きかえをしたりしましょう。また、平方の差を利用することによっても問題を解くことができます。
式の展開と因数分解では、問題を解く手順があります。どのような方法によって問題を解けばいいのか理解するようにしましょう。






