円と直線の関係を利用する定理は複数あります。その中の一つが方べきの定理です。方べきの定理は高校数学で必ず覚えなければいけない内容です。
方べきの定理を利用すれば、辺の長さを計算することができます。方べきの定理を証明するのは難しくなく、相似を利用することによって証明可能です。
なお方べきの定理は大きく3つの種類があります。そこで、すべての種類を覚えましょう。また辺の長さの計算だけでなく、証明問題を解かなければいけないことがあります。このとき方べきの定理だけでなく、方べきの定理の逆についても利用できるようにしましょう。
高校数学で学ぶ内容が方べきの定理です。ここでは、方べきの定理の内容や証明問題を解説していきます。
もくじ
方べきの定理は3つに分けることができる
一つの円に対して、2本の直線がある場合は方べきの定理を利用できるかどうか考えましょう。円と直線を利用する定理が方べきの定理になります。
このとき、方べきの定理は大きく以下の3つに分けることができます。
- 円の内部に点Pを取る
- 円の外部に点Pを取る
- 円の外部に点Pを取り、接線を引く
すべて方べきの定理であり、考え方はどれも同じです。ただ図形の見た目が異なります。そこで、すべてのパターンで方べきの定理を利用できるようになりましょう。
円の内部に点Pを取る場合の方べきの定理
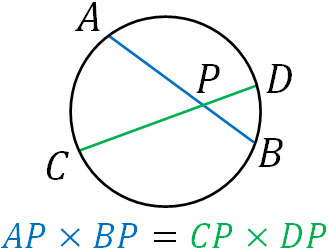
まず、円の内部に点Pを取るケースを考えてみましょう。方べきの定理では、点Pを通る2つの直線について、以下の関係が成り立ちます。
証明する方法は簡単であり、円周角の定理を利用します。以下の図を作れば、2つの角が等しいため、△APCと△DPBは相似であるとわかります。
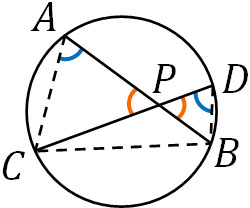
相似図形であるため、AP:DP=CP:BPです。そのため、方べきの定理を証明することができました。
- \(AP×BP=CP×DP\)
円の外部に点Pを取る場合の方べきの定理
先ほど、円の内部に点Pがある場合の方べきの定理を解説しました。一方、円の外部に点Pがある場合はどのように考えればいいのでしょうか。この場合、方べきの定理は以下のようになります。
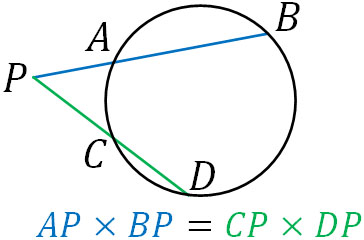
先ほど解説した内容に比較して、公式は同じく\(AP×BP\)\(=CP×DP\)です。また同じ直線を利用し、点Pとの距離をかける点についても同じです。図の見た目は変わるものの、同じ定理というわけです。
証明方法については、以下の図を作りましょう。
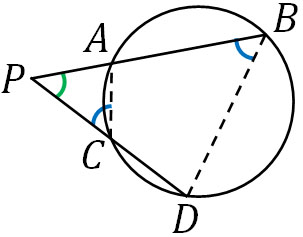
△APCと△DPBについて、∠Pは共通です。また、ABCDは円に内接する四角形なので∠B=∠ACPです。2つの角が等しいため、△APCと△DPBは相似です。そのためAP:DP=CP:BPとなり、\(AP×BP=CP×DP\)を証明できました。
円の外部に点Pを取り、接線を引くケースの方べきの定理
円の外部に点Pを置くケースを先ほど解説しました。このとき、点Pから一つの接線を引くケースでは、方べきの定理は以下のようになります。
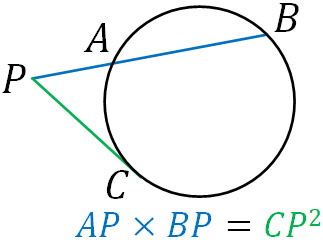
ただ、先ほど記した\(AP×BP=CP×DP\)と意味は同じです。Cは接点であるため、以前の図にあった点Dが存在しません。そこで、CPを二乗するのです。
証明方法はこれまで説明した方法と同じであり、相似図形を利用します。以下の図を作りましょう。
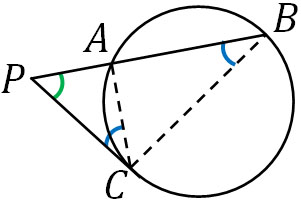
△APCと△CPBについて、∠Pは共通です。また接弦定理より、∠ACP=∠Bです。2つの角が等しいため、△APCと△CPBは相似です。つまり、AP:CP=CP:BPです。こうして、\(AP×BP=CP^2\)を証明できました。
方べきの定理を利用し、練習問題を解く
それでは、実際に方べきの定理を利用して問題を解いてみましょう。以下の答えは何でしょうか。
- 点Oが円の中心のとき、\(x\)の値を求めましょう。
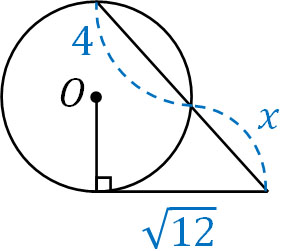
方べきの定理を利用して計算すると以下のようになります。
\(x(x+4)=12\)
\(x^2+4x-12=0\)
\((x+6)(x-2)=0\)
\(x>0\)なので、\(x=2\)が正解であるとわかります。
方べきの定理の逆を利用して証明問題を解く
方べきの定理を学んだら、次に方べきの定理の逆を理解しましょう。方べきの定理では、以前の図において、以下が成り立つと解説しました。
- \(AP×BP=CP×DP\)
- \(AP×BP=CP^2\)
それでは、\(AP×BP=CP×DP\)または\(AP×BP=CP^2\)となる場合、どのように考えればいいのでしょか。この場合、方べきの定理の逆を利用できます。
\(AP×BP=CP×DP\)が成立する場合、4つの点(A、B、C、D)は一つの円周上に存在します。また\(AP×BP=CP^2\)が成り立つ場合、3つの点(A、B、C)は一つの円周上に存在し、Cは接点です。これが方べきの定理の逆です。
応用問題で出される方べきの定理の逆
それでは、方べきの定理の逆を利用して証明問題を解いてみましょう。応用問題として、方べきの定理の逆を利用する問題が出されます。4つ(または3つ)の点が円周上にあることを証明する問題の場合、方べきの定理の逆を利用できないかどうかを考えましょう。
以下の問題の答えは何でしょうか。
- 2つの円が点Qで接しており、共通接線上に点Pを置きます。Pからそれぞれの円に対して以下のように線を引き、それぞれの点をA、B、C、Dとします。このとき、A、B、C、Dが一つの円周上に存在することを証明しましょう。
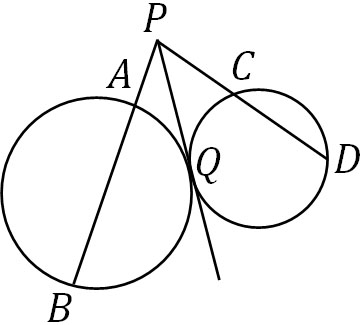
4つの点が円周上に存在することを証明すればいいため、方べきの定理の逆を利用すればいいと理解できます。そこで方べきの定理を利用すると、左側の円では以下の式を作ることができます。
\(AP×BP=QP^2\)
次に右側の円に着目すると、以下の式を作ることができます。
\(CP×DP=QP^2\)
こうして、以下の式を作れます。
\(AP×BP=CP×DP\)
方べきの定理の逆よりA、B、C、Dは一つの円周上に存在することを証明できました。
方べきの定理を利用して辺の長さを計算する
円と直線の関係を利用する定理が方べきの定理です。方べきの定理は高校数学で必ず覚えなければいけない内容です。
方べきの定理を利用することにより、辺の長さを計算することができます。また証明問題で方べきの定理が出されることがあります。
なお方べきの定理を学んだあと、方べきの定理の逆も理解しましょう。方べきの定理を当てはめることができる場合、4つの点(または3つの点)は一つの円周上に存在します。方べきの定理の逆を利用する証明は応用問題です。
ここまで解説した内容を理解し、方べきの定理を利用しましょう。円と直線の問題が出されたとき、方べきの定理を利用できるかどうか考えるといいです。






