私たちが物理で熱力学を学ぶ理由として、多くの場面で熱力学が応用されているからです。熱力学の中でも、最も身近な応用例が熱機関です。
熱を利用して動いている機器類は非常に多いです。ガソリン機関やディーゼル機関、発電所など、熱エネルギーを動力へ変換するのです。こうした熱機関で重要になるのが、どれだけ効率的にエネルギーを得ることができるのかを表す熱効率です。
熱機関では、石油などのエネルギーを燃やすことによって熱を得て、一部が仕事に利用され、残りは熱として外部へ放出されます。その後、元の状態に戻って再びエネルギーを燃やして熱を得ます。これを繰り返すことによって動力として働くのです。
それでは、どのように熱機関での熱効率を計算すればいいのでしょうか。私たちの生活で大きな役割を果たしている熱機関について、熱効率の概要や計算方法を解説していきます。
もくじ
熱力学で重要な熱機関
動力として働くためには、エネルギーを与えなければいけません。熱エネルギーによって動く機器類は多いのです。ただ熱を与えることで熱機関を動かすとき、すべての熱エネルギーが仕事に利用されるわけではありません。一部は仕事に利用されるものの、残りの熱エネルギーは外部へ排出されます。
そのため、熱機関は以下のサイクルを繰り返します。
- 熱エネルギーを得る
- 仕事をする
- 仕事に利用されなかった熱エネルギーを外へ排出する(元の状態に戻る)
例えば石油を燃やすことにより、以下のようになります。
- 石油を燃やし、100Jを得る
- 20Jを仕事に利用する
- 80Jを外部に放出する
熱を利用する場合、すべてがこのサイクルとなります。
例えばストーブを利用する場合、発生した熱のすべてが部屋を暖めるために利用されるわけではありません。熱を発生させると一酸化炭素などの有毒物質も発生するため、ストーブを利用する場合は煙突から有害物質を放出させます。同時に、大部分の熱も煙突から外部へ放出されます。

発生させた熱のうち、部屋を暖めるために利用される熱は一部です。これは、熱機関も同じです。私たちの生活で熱を利用するとき、必ず外部へ放出される熱が発生するのです。
熱効率の計算方法と公式
それでは、どのように熱効率を計算すればいいのでしょうか。物理では公式を覚えても意味がないため、公式を作れるようになりましょう。
熱効率というのは、「加えた熱のうち、どれだけを仕事に利用されたのか」を表します。例えば100Jを加え、そのうち20Jが仕事に利用されたのであれば、熱効率は0.2です。そのため加えた熱量を\(Q_{in}\)、仕事量を\(W\)とすると、熱効率\(e\)は以下の公式で表すことができます。
- \(e=\displaystyle\frac{W}{Q_{in}}\)
熱効率の意味を理解すれば、公式を覚えなくてもこの式を作ることができます。
また仕事というのは、加えた熱量\(Q_{in}\)から外部へ放出された熱量\(Q_{out}\)を引くことによって得ることができます。そのため、熱効率の公式を以下のように記すこともできます。
- \(e=\displaystyle\frac{Q_{in}-Q_{out}}{Q_{in}}\)
熱効率を計算するとき、これらの公式を利用することによって問題を解きましょう。
熱機関の熱効率を計算する練習問題
なお熱効率を学ぶとき、実際に計算問題を解かなければ理解できません。そこで、熱機関に関する練習問題を解説していきます。以下の問題の答えは何でしょうか。
- なめらかに動くピストンをもつシリンダーに物質量\(n\)の気体(理想気体の単原子分子)を入れ、図のように気体の状態を「A→B→C→D→A」の順に変化させます。この気体の定積モル比熱を\(C_V\)、点Aでの温度を\(T_A\)、気体定数を\(R\)とします。
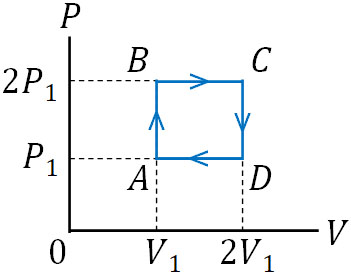
- 点B、点C、点Dでの温度はいくらですか。
- A→B、B→C、C→D、D→Aについて、定積モル比熱\(C_V\)を用いて気体に与えられた熱量(または気体から放出された熱量)を計算しましょう。
- この熱機関が「A→B→C→D→A」と1サイクルするとき、\(n,T_A,R\)を用いて気体が行う仕事量を表しましょう。
- この熱機関の熱効率を有効数字3ケタで求めましょう。
熱機関の計算問題では、熱効率の公式を暗記しても解くことはできません。複合問題が出されるため、熱力学で学んだすべての知識を利用する必要があります。
ボイル・シャルルの法則を利用し、温度を計算する
気体の出入りがない場合、ボイル・シャルルの法則を利用することができます。あらゆるケースでボイル・シャルルの法則を利用することができるため、気体の圧力や体積、温度を計算したい場合はボイル・シャルルの法則を活用しましょう。
1) 点B、点C、点Dでの温度はいくらですか
ボイル・シャルルの法則より、以下のように計算できます。
・点Bの温度\(T_B\)
\(\displaystyle\frac{P_1V_1}{T_A}=\displaystyle\frac{2P_1·V_1}{T_B}\)
\(T_B=2T_A\)
・点Cの温度\(T_C\)
\(\displaystyle\frac{P_1V_1}{T_A}=\displaystyle\frac{2P_1·2V_1}{T_C}\)
\(T_C=4T_A\)
・点Dの温度\(T_D\)
\(\displaystyle\frac{P_1V_1}{T_A}=\displaystyle\frac{P_1·2V_1}{T_D}\)
\(T_D=2T_A\)
こうして、それぞれの点の温度を得ることができました。
定積変化、定圧変化で利用されるマイヤーの関係式
次に、定積モル比熱\(C_V\)を用いて加えられた熱量(または放出された熱量)を計算します。図を確認すると、定積変化と定圧変化が存在します。定積変化と定圧変化を学ぶとき、マイヤーの関係式を知ることになります。
以下がマイヤーの関係式です。
- \(C_P=C_V+R\)
この式が成り立つ理由として、理想気体の単原子分子では定積モル比熱と定圧モル比熱は以下の式で表すことができるからです。
- \(C_V=\displaystyle\frac{3}{2}R\)
- \(C_P=\displaystyle\frac{5}{2}R\)
こうした関係性があることを復習して、熱機関に関する今回の問題を解きましょう。
2) A→B、B→C、C→D、D→Aについて、定積モル比熱\(C_V\)を用いて気体に与えられた熱量(または気体から放出された熱量)を計算しましょう
それぞれの変化について、熱量を計算していきます。
・A→Bの熱量\(Q_{AB}\)
A→Bは定積変化です。またモル比熱\(C\)を利用する場合、熱量\(Q\)を表す公式は以下になります。
- \(Q=nCΔT\)
そこで、この公式に当てはめましょう。
\(Q_{AB}=nC_V(2T_A-T_A)\)
\(Q_{AB}=nC_VT_A\)
・B→Cの熱量\(Q_{BC}\)
B→Cは定圧変化です。問題文では、定積モル比熱\(C_V\)しか与えられていません。そこでマイヤーの関係式を利用しましょう。\(C_P=C_V+R\)を利用すると、以下のように熱量\(Q_{BC}\)を計算できます。
\(Q_{BC}=n(C_V+R)(4T_A-2T_A)\)
\(Q_{BC}=2nT_A(C_V+R)\)
・C→Dの熱量\(Q_{CD}\)
C→Dは定積変化です。
\(Q_{CD}=nC_V(2T_A-4T_A)\)
\(Q_{CD}=-2nC_VT_A\)
・D→Aの熱量\(Q_{DA}\)
D→Aは定圧変化です。
\(Q_{DA}=n(C_V+R)(T_A-2T_A)\)
\(Q_{DA}=-nT_A(C_V+R)\)
こうして、それぞれの変化で気体に与えられた熱量、または気体から放出された熱量を計算することができました。
\(P-V\)グラフの面積が仕事\(W\)になる
定圧変化では、\(W=PΔV\)によって仕事を計算できます。また定積変化では、仕事は行われません。気体の体積が増えるまたは減ることにより、気体による仕事量を計算できるのです。
重要なのは、\(P-V\)グラフの面積が仕事\(W\)になる事実です。そのため仕事量\(W\)を計算するとき、熱機関が1サイクルするときの面積に着目しましょう。
3) この熱機関が「A→B→C→D→A」と1サイクルするとき、\(n,T_A,R\)を用いて気体が行う仕事量を表しましょう
図より、四角形で囲まれている面積は\(P_1V_1\)です。つまり、\(W=P_1V_1\)となります。そこで\(P_1V_1\)について、\(n,T_A,R\)を用いて表しましょう。
気体の状態方程式より、\(PV=nRT\)です。そのため、以下のようになります。
- \(P_1V_1=nRT_A\)
こうして、気体が行う仕事量は\(nRT_A\)とわかりました。
得た熱量\(Q_{in}\)と仕事\(W\)を利用し、熱効率を計算する
ここまでの計算をすることにより、ようやく熱効率を得ることができます。得た熱量\(Q_{in}\)と仕事\(W\)を利用することにより、熱効率を計算できるのです。
4) この熱機関の熱効率を有効数字3ケタで求めましょう。
それぞれの過程で気体に与えられた熱量(または気体から放出された熱量)を記すと、先ほどの計算結果より以下のようになります。
- \(Q_{AB}=nC_VT_A\)
- \(Q_{BC}=2nT_A(C_V+R)\)
- \(Q_{CD}=-2nC_VT_A\)
- \(Q_{DA}=-nT_A(C_V+R)\)
つまり、気体に加えられた熱量\(Q_{in}\)は\(Q_{AB}\)と\(Q_{BC}\)です。
\(Q_{in}=Q_{AB}+Q_{BC}\)
\(=nC_VT_A+2nT_A(C_V+R)\)
\(=3nC_VT_A+2nRT_A\)
気体に加えられた熱量\(Q_{in}\)と仕事\(W\)がわかっているため、熱効率\(e\)を計算しましょう。
\(e=\displaystyle\frac{W}{Q_{in}}\)
\(=\displaystyle\frac{nRT_A}{3nC_VT_A+2nRT_A}\)
\(=\displaystyle\frac{R}{3C_V+2R}\)
こうして、熱効率は\(e=\displaystyle\frac{R}{3C_V+2R}\)とわかりました。
なお前述の通り、理想気体の単原子分子では\(C_V=\displaystyle\frac{3}{2}R\)です。そこで、\(C_V=\displaystyle\frac{3}{2}R\)を代入しましょう。
\(e=\displaystyle\frac{R}{3C_V+2R}\)
\(e=\displaystyle\frac{R}{3×\displaystyle\frac{3}{2}R+2R}\)
\(e=\displaystyle\frac{2}{13}\)
\(e≒0.1538\)
こうして、熱効率は0.154(15.4%)とわかります。練習問題を解くと、「熱機関では熱力学で学んだ内容をすべて利用して問題を解かなければいけない」とわかります。熱効率に関する問題が難しいのは、複合問題になるからなのです。
参考までに、乗用車エンジンの熱効率は0.4~0.5ほどです。つまり仕事に利用されるエネルギーは40~50%ほどであり、ほとんどの熱は外部へ放出されることになります。火力発電でも、熱効率は0.5ほどです。熱効率を改善し、外部へ放出される熱量を減らすのは難しいのです。
すべての熱力学の知識を利用して熱効率を学ぶ
熱効率の概念はシンプルです。加えられた熱量\(Q_{in}\)に対して、気体が行った仕事\(W\)の割合を計算することによって熱効率を得ることができます。また気体に加えられた熱量\(Q_{in}\)から、気体から放出された熱量\(Q_{out}\)を引くことによっても仕事\(W\)を得られます。
熱効率の公式を覚えてはいけません。熱効率の定義を学び、公式を作れるようにしましょう。そうすれば、熱効率の計算が可能です。
ただ熱機関に関する問題を解くとき、多くのケースで複合問題となります。熱力学で学んだすべての知識を利用する必要があり、ボイル・シャルルの法則やモル比熱、\(P-V\)グラフの知識を利用して熱効率を計算しましょう。
さまざまな知識を利用する必要があるため、熱効率の問題は難しいです。そこで、どのように問題を解けばいいのか学びましょう。






