母集団が正規分布しているかどうか不明な場合、ノンパラメトリック検定を利用します。こうしたノンパラメトリック検定としてマン・ホイットニーのU検定(ウィルコクソンの順位和検定)があります。
対応のない二標本t検定に相当するのがマン・ホイットニーのU検定です。マン・ホイットニーのU検定とウィルコクソンの順位和検定は名前が違うだけで、基本的に同じと考えましょう。
母集団の正規分布に関係なく、対応のないすべての標本について検定できるのがマン・ホイットニーのU検定です。つまり、あらゆる場面でマン・ホイットニーのU検定を利用できるというわけです。
それでは、どのようにしてマン・ホイットニーのU検定(ウィルコクソンの順位和検定)を利用すればいいのでしょうか。検定をするとき、事前に概念や計算法を理解しなければいけません。そこで、マン・ホイットニーのU検定の計算方法を解説していきます。
もくじ
対応のないt検定に相当するノンパラメトリック検定
統計学で最も重要なのがt検定です。ただt検定をするとき、対応のある二標本t検定と対応のない二標本t検定があり、それぞれ計算方法が異なります。
そうした中でも、対応のないt検定に相当するノンパラメトリック検定がマン・ホイットニーのU検定です。t検定は母集団が正規分布しているという前提で利用できます。母集団が正規分布しているときに利用できる検定法がパラメトリック検定です。
一方で母集団が正規分布しているかどうか不明なケースがあり、その場合はノンパラメトリック検定を利用します。マン・ホイットニーのU検定はノンパラメトリック検定であり、母集団のグラフの形に関係なく利用することができます。
データの中に異常値(外れ値)が含まれていたり、母集団が正規分布するかどうか不明だったりする場合はマン・ホイットニーのU検定を活用しましょう。
マン・ホイットニーのU検定とウィルコクソンの順位和検定は同じ
なお多くの人が混乱することとして、マン・ホイットニーのU検定とウィルコクソンの順位和検定があります。この違いについて、前述の通り名前が違うだけで2つとも中身は同じです。つまり、同一の検定法と理解しましょう。
一方でウィルコクソンの符号順位検定という方法もあります。マン・ホイットニーのU検定(ウィルコクソンの順位和検定)に対して、ウィルコクソンの符号順位検定はまったくの別物です。
違いとしては、以下のように考えましょう。
- 対応のないt検定に相当するノンパラメトリック検定:マン・ホイットニーのU検定(ウィルコクソンの順位和検定)
- 対応のあるt検定に相当するノンパラメトリック検定:ウィルコクソンの符号順位検定
両方ともノンパラメトリック検定です。ただ対応のある標本なのか、対応のない標本なのかによって利用する検定法が変わります。
統計量Uの求め方と順位付けのルール
それでは、どのようにマン・ホイットニーのU検定をすればいいのでしょうか。まず、マン・ホイットニーのU検定をするときの概念を理解しましょう。
マン・ホイットニーのU検定では、統計量Uを計算します。統計量Uの求め方としては、片方のデータの点に着目して、それぞれの点よりも大きいデータがいくつあるのかを数えましょう。このときはそれぞれの順位付けをして、以下のように順位の低いサンプルの数を計算します。
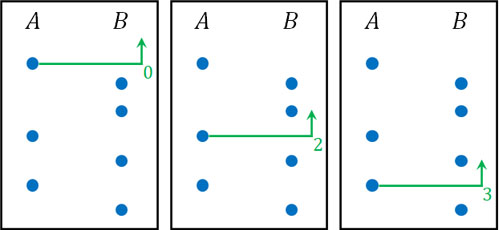
Aに着目すると、一番上の点よりも低い順位のBの点はなく0です。次に真ん中の点に着目すると、そこより低い順位のBの点は2つです。一番下の点であれば、そこより低い順位のBの点は3つです。こうして、低い順位がいくつあるのかをそれぞれ確認しましょう。
このとき統計量Uが非常に小さい、または非常に大きい場合は差があるといえます。
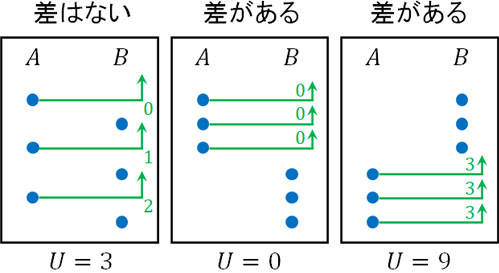
なお差があるとき、どちらを基準にしてもいいです。ただ計算が楽なほうを採用しましょう。例えば以下の場合、どちらを利用しても検定の結果は同じになるものの、統計量Uが小さいと計算が楽です。
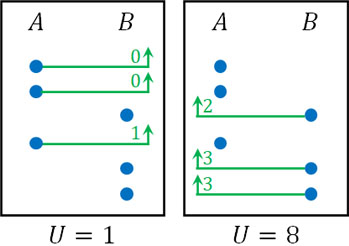
なお統計量Uを求めるとき、順位が同じになるケースがあります。この場合、「値がわずかに小さい場合」と「値がわずかに大きい場合」の2パターンを考え、平均値を求めましょう。以下のようになります。
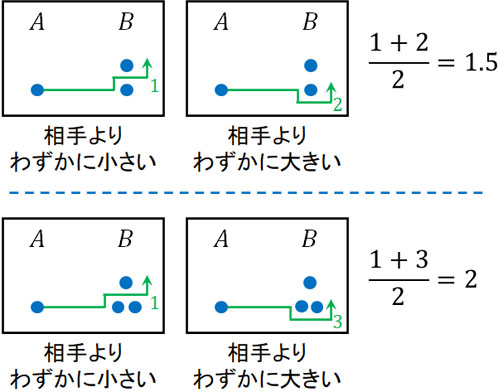
低い順位がいくつあるのかを数えるとき、平均値を利用するといいです。
小標本では統計量Uを計算し、確率を求める
それでは、実際にマン・ホイットニーのU検定(ウィルコクソンの順位和検定)をしてみましょう。このとき小標本なのか、大標本なのかによって確率を求める方法が異なります。対応のない標本について、2つの群のサンプル数が両方とも20以下の場合、小標本とみなして計算しましょう。
このときは統計量Uを求めましょう。また、統計学の教科書に記載されているマン・ホイットニーのU検定表を利用して、両側確率が0.05(5%)となる統計量Uと比較するといいです。
例えば、以下の問題の答えは何でしょうか。
- 大学Aと大学Bがスポーツ競技し、それぞれの種目での結果は以下の通りでした。大学Aと大学Bに実力差はあるでしょうか。

まず、帰無仮説と対立仮説を設定しましょう。
- 帰無仮説:大学Aと大学Bに差はない
- 対立仮説:大学Aと大学Bに差がある
次に、順位ごとに並べましょう。その後、計算が楽なほうに着目して統計量Uを計算します。以下のようになります。
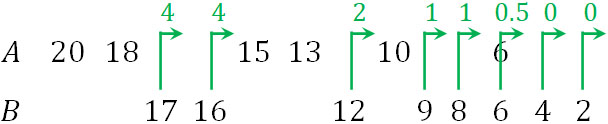
この場合、統計量Uは以下のようになります。
\(U=0.5+1+1+2+4+4=12.5\)
今回はBに着目しましたが、Aに着目して統計量Uを計算しても問題ありません。どちらであっても、検定による答えは同じになります。参考までに、Aに着目するときの統計量Uは35.5です。
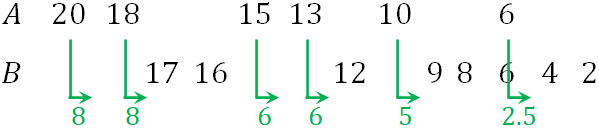
つまり、この標本のU値は12.5~35.5です。そこで有意水準0.05となるU値と比較し、値の大小を比較しましょう。サンプル数を確認すると、大学Aは\(n_1=6\)、大学Bは\(n_2=8\)です。このとき\(P=0.05\)となるU値は8です。
つまり統計量Uが8よりも小さい場合、5%以下の確率で発生する稀な結果が起こったと判断できます。ただ統計量Uは12.5であり、0.05となるU値よりも大きいです。そのため帰無仮説を棄却できず、大学Aと大学Bに実力差はないと結論付けることができます。
もう一方の有意点Uを見つける計算方法
なお統計量Uというのは、\(n_1×n_2=U_1+U_2\)で計算できる性質があります。今回の場合、前述の通り大学Aは\(n_1=6\)、大学Bは\(n_2=8\)です。また両側確率で\(P=0.05\)となるU値は8です。そのため、両側確率でもう一方の\(P=0.05\)となるポイントは以下の式によって計算できます。
\(U_2=n_1×n_2-U_1\)
\(U_2=6×8-8\)
\(U_2=6×8-8\)
\(U_2=40\)
つまり、計算したU値が\(U≦8\)または\(U≦40\)の場合、5%以下で発生する稀な現象が起こっていると判断します。ただ今回の場合、一つの統計量Uは12.5であり、もう一方のU値は35.5です。
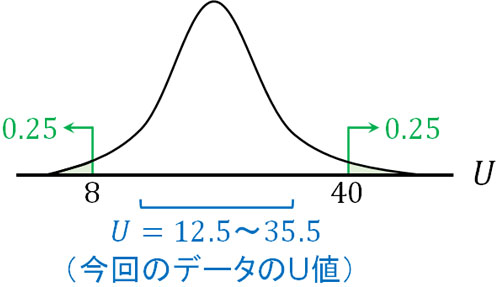
こうしたグラフを利用すれば、統計量Uを利用して確率の計算をする意味を理解できると思います。統計量Uを計算した後、U値が両側確率で0.05の範囲に含まれているかどうかを確認することによって、帰無仮説を棄却できるかどうかを判断できます。
大標本では標準正規分布を利用して確率を得る
それでは小標本ではなく、大標本の場合はどのように考えればいいのでしょうか。一方の標本について、サンプル数が多くなる場合は標準正規分布を利用して確率を計算しましょう。サンプル数\(n\)が多くなる場合、正規分布へ近似できるからです。
正規分布を利用して確率を計算するためには平均値\(μ\)と標準偏差\(σ\)を計算しなければいけません。このとき、サンプル数を\(n_1\)・\(n_2\)とするとき、平均値\(μ\)と標準偏差\(σ\)は以下の公式によって得ることができます。
- \(μ=\displaystyle\frac{n_1×n_2}{2}\)
- \(σ=\sqrt{\displaystyle\frac{n_1×n_2×(n_1+n_2+1)}{12}}\)
なぜこの計算式になるのかは解説しません。数学者が考えてくれた公式であるため、ありがたく利用させてもらいましょう。
また正規分布を利用して確率の計算をするとき、標準正規分布へ変換しなければいけません。そこで標準正規分布の確率変数\(Z\)を得るため、以下の公式を利用しましょう。
- \(Z=\displaystyle\frac{U-μ}{σ}\)
確率変数\(Z\)を得ることができれば、標準正規分布表から確率を得ることができます。
それでは、実際に例題を解いてみましょう。以下の問題の答えは何でしょうか。
- サッカー部とテニス部で部員の体力測定をした結果が以下です。サッカー部とテニス部で体力差はあるでしょうか。
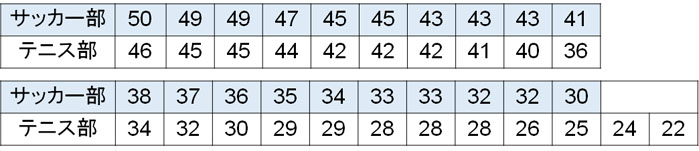
帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:サッカー部とテニス部で差はない
- 対立仮説:サッカー部とテニス部で差がある
そこで、以下のように順位を利用して統計量Uを計算しましょう。
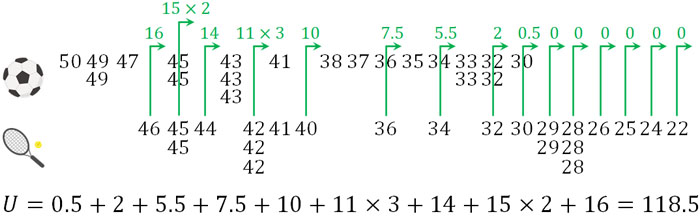
こうして、統計量Uは118.5になるとわかりました。次に、先ほど提示した公式を利用して平均値\(μ\)と標準偏差\(σ\)を計算しましょう。
\(μ=\displaystyle\frac{20×22}{2}=220\)
\(σ=\sqrt{\displaystyle\frac{20×22×43}{12}}≒39.7\)
そこで標準正規分布を利用して、確率変数\(Z\)を計算しましょう。
\(Z=\displaystyle\frac{U-μ}{σ}\)
\(Z=\displaystyle\frac{118.5-220}{39.7}\)
\(Z≒-2.56\)
標準正規分布で\(Z=-2.56\)となるとき、両側確率はいくらでしょうか。統計学の教科書には標準正規分布表が掲載されているはずです。そこでマイナスを取り除き、\(Z=2.56\)となる確率を探しましょう。そうすると、0.01046(1.046%)であるとわかります。
つまり有意水準を0.05とすると、今回は0.05(5%)よりも低い確率で発生する稀な事象が発生したと判断できます。そこで帰無仮説を棄却し、対立仮説を採用します。こうして、サッカー部とテニス部では体力に差があると判断できます。
対応のない二標本を利用し、ノンパラメトリック検定を行う
ノンパラメトリック検定としてマン・ホイットニーのU検定があります。マン・ホイットニーのU検定とウィルコクソンの順位和検定は同じであり、違いはありません。ただウィルコクソンの符号順位検定は異なる検定法なので区別しましょう。
マン・ホイットニーのU検定では、必ず統計量Uを計算しなければいけません。そこで、数字の大きい順(または小さい順)に並べましょう。こうして順位付けをすれば、たとえ外れ値があっても問題なく検定できます。
すべての対応のない二標本に対して、検定可能な方法がマン・ホイットニーのU検定です。このときマン・ホイットニーのU検定で差があると判断できる場合、検定法がt検定でなくてもそれで問題ないのです。
母集団の正規分布に関係なく利用できる便利な統計手法がマン・ホイットニーのU検定(ウィルコクソンの順位和検定)です。そこで原理を理解し、対応のない二標本を利用してノンパラメトリック検定を行えるようにしましょう。