平均値・中央値・最頻値：度数分布表・ヒストグラムでの代表値

統計では数値を読み解かなければいけません。つまり、データがどのような意味をもつのか理解するのです。

データを見やすくまとめた表やグラフとして度数分布表とヒストグラムがあります。また統計データを取り扱うとき、度数分布表とヒストグラムを利用して平均値や中央値、最頻値を出します。これによって、データを正確に読み解けるようになります。

平均値や中央値、最頻値を代表値といいます。そのためこれらの値は重要です。それでは、なぜ平均値だけでなく中央値や最頻値を学ばないといけないのでしょうか。また、これらの値は何を意味しているのでしょうか。

統計を学ぶとき、新たな言葉を理解しなければいけません。そこで平均値や中央値、最頻値の概念や値の出し方を含めて解説していきます。

データを度数分布表とヒストグラム（柱状グラフ）で表す

多くの場合、データを得るときはランダムな数字を得られます。例えば体重を測定するとき、以下のようなデータを得られます。

多くの場合、最初に得られるデータは数字のみです。そこで、数字を解析しやすくするために表や図にしましょう。データを表にしたのが度数分布表であり、図にしたのがヒストグラム（柱状グラフ）です。

度数分布表では、例えば以下のような表になります。

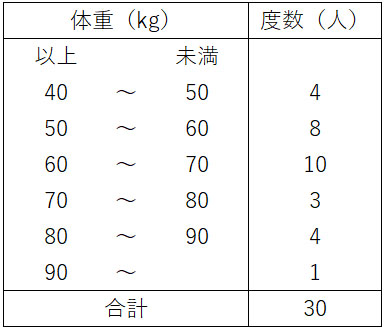
数字を確認しても、データが何を表しているのか理解しにくいです。一方でこのように度数分布表として整理すれば、データが何を意味しているのか理解できるようになります。

また度数分布表を棒グラフにした図をヒストグラム（柱状グラフ）といいます。ヒストグラムを利用すれば、どの値に多くのデータが集まっているのか把握できます。以下がヒストグラムです。

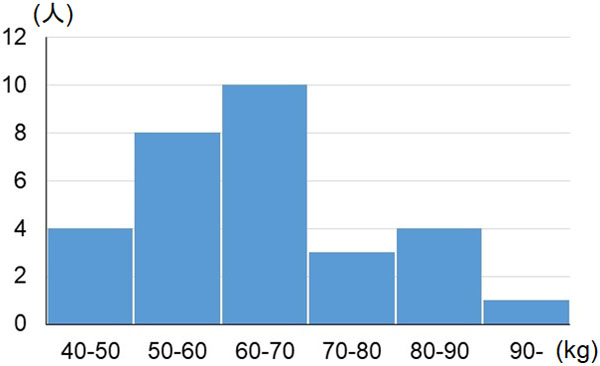
度数分布表よりも、ヒストグラムのほうがデータを読み解きやすいです。そのため資料を作り、誰か他の人にデータを説明するときは度数分布表よりもヒストグラムが頻繁に利用されます。

ドットプロットを利用するグラフ

なおデータの数が少ない場合、度数分布表やヒストグラムではなく、ドットプロットを利用してグラフを作ることもあります。点（ドット）を利用することによってグラフを描くのです。

以下がドットプロットになります。

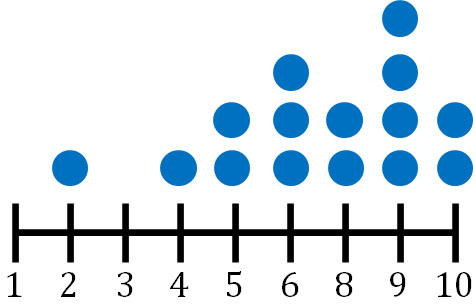
例えばこのドットプロットが10点満点のテストを表しているであれば、10点を取った人が2人いるとドットプロットからわかります。ヒストグラムと似ているグラフであり、点を利用するグラフがドットプロットです。統計データを確認するとき、ドットプロットを利用することもあります。

平均値、中央値（メジアン）、最頻値（モード）の意味

こうして統計データを得られた後、そのデータが何を意味しているのか解析しなければいけません。このとき頻繁に利用されるのが平均値や中央値、最頻値です。データの特徴を一つの数字で表す場合、その数字を代表値といいます。平均値や中央値、最頻値は代表値です。

平均値については、すでに理解していると思います。すべてのデータの値を足した後、合計個数でわることによって平均値を得ることができます。例えば、以下のデータがあるとします。

• 1, 2, 5, 6, 8

このデータの平均値は4.4です。

• \((1+2+5+6+8)÷5=4.4\)

こうして、合計の数に対して個数でわることで平均値をだしましょう。

中央値（メジアン）は真ん中の数字を表す

一方、中央値（メジアン：median）とは何でしょうか。データを並べるとき、真ん中の値を中央値といいます。先ほどと同じように、以下のデータがあるとします。

• 1, 2, 5, 6, 8

データを確認すると、「1, 2, 5, 6, 8」がデータであるため、中央値は5です。

注意点として、データの数が偶数の場合は中央値の出し方が少し複雑になります。データの数が奇数の場合、先ほどの例のようにデータの真ん中にある値が中央値です。一方、以下の場合の中央値は何でしょうか。

• 1, 2, 3, 4

データの数が偶数であるため、真ん中に数字がありません。この場合、真ん中にある2つのデータの平均値を中央値にしましょう。

先ほどのデータであれば、「1, 2, 3, 4」がデータであるため、真ん中にある2つのデータは2と3です。そこで、2と3の平均値を中央値にしましょう。2と3の平均値は2.5です。そのため、中央値は2.5になります。

最も多くの個数を含む群の値が最頻値（モード）

ほかにも頻繁に利用される代表値があり、それが最頻値（モード：mode）です。データの中で、どの値が最も頻繁に表れるのかを指し示すのが最頻値です。

最頻値を理解するため、先ほどのヒストグラムを以下に再び掲載します。

このようにヒストグラムを確認すると、60～70kgの人が最も多いとわかります。こうして、最頻値は60～70kgの階級値（階級の端と端の値を平均した数字）を利用して65kgとわかります。

異常値（外れ値）により、平均値以外の代表値が重要になる

それでは、なぜ代表値が複数あるのでしょうか。平均値だけでなく、中央値や最頻値を利用するのでしょうか。この理由として、平均値ではデータを正しく表現できないことが多いからです。

平均値が代表値として機能する条件として、左右対称のヒストグラムになることが挙げられます。

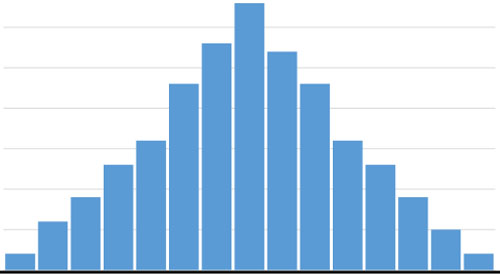
このような左右対称のヒストグラムでは、平均値と中央値、最頻値が一致します。こうした左右対称にデータが分布している状態を正規分布といいます。正規分布のとき、平均値は信用できる代表値です。

ただ統計データを取るとき、必ずしも左右対称になるとは限りません。また、データに異常値（外れ値）が含まれるケースは多いです。異常値とは、異常に大きい値（または小さい値）を指します。

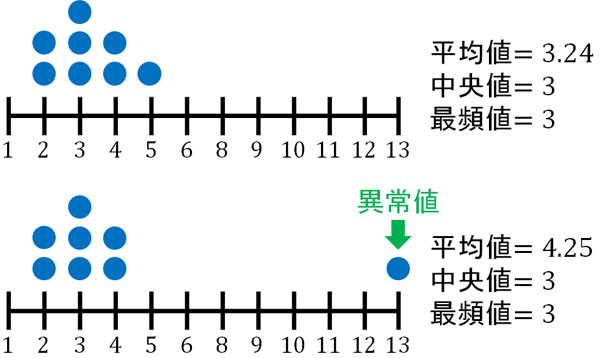
異常値が存在すると、平均値の値が大きくなります（または小さくなります）。そのため、平均値は本来のデータを表すことができなくなります。

一方、中央値や最頻値であれば異常値が含まれていても値はほとんど変わりません。これが、統計データの解析で中央値や最頻値が代表値として頻繁に利用される理由です。

平均値が意味のない実際の例

平均値が役に立たないわかりやすい例としては平均年収や平均貯蓄額があります。多くの人は年収や貯蓄額が高くありません。それにも関わらず平均年収や平均資産額では、高い数字が統計データとして出されます。この理由として、一部の富裕層が平均年収や平均貯蓄額を押し上げているからです。

つまり年収や貯蓄額の統計データを確認するとき、富裕層による異常値がたくさんあるため、結果として平均年収や平均貯蓄額をみても人々の実情を知ることはできないのです。事実、平均年収は以下のように左右対称のヒストグラムになっておらず、グラフには多くの異常値が現れます。

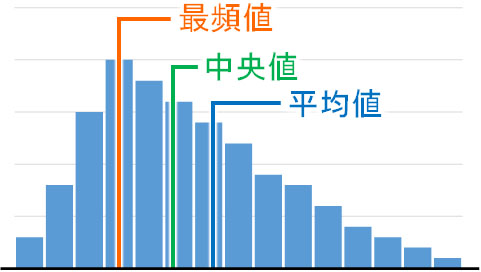
そのため平均年収や平均貯蓄額を知るのは意味がなく、このデータで最も重要なのは中央値と最頻値です。ヒストグラムが左右対称でない場合、平均値は役に立ちません。

統計データを取り扱うとき、なぜ中央値や最頻値が重要になるのか理解しましょう。

ヒストグラムの形によって平均値と中央値の場所が変わる

データが正規分布せず、左右対称ではない場合、このように平均値や中央値、最頻値の値がずれます。こうしたヒストグラムは多く、異常値がどこに多いのかによってグラフの形が変わってきます。

グラフの右側に異常値が多い場合、平均値や中央値は右へずれるようになります。一方でグラフの左側に異常値が多い場合、平均値や中央値は左へずれるようになります。ただ、中央値のずれは平均値に比べて大きくなりません。

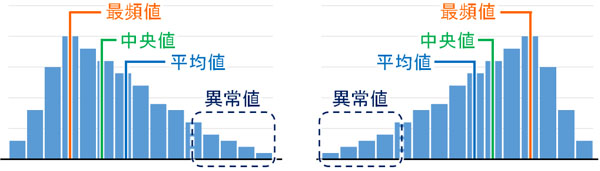
平均年収や平均貯蓄額の場合、富裕層による異常値が多いです。そのため、平均値は右へずれます。その結果、平均値を確認しても意味がないデータとなるのです。

私たちは日常生活で平均を頻繁に利用します。ただ統計で平均値を確認しても意味ないことは多く、グラフの形が正規分布ではない場合、中央値や最頻値を確認しなければいけません。この理由は、中央値と最頻値は外れ値の影響を受けにくいからです。

言葉の意味を理解し、統計データを読む

統計データを読むとき、事前に言葉の意味を理解しなければいけません。平均値については全員がすでに知っているものの、統計を学んでいない人にとっては、中央値や最頻値という言葉を新たに学ぶことになります。

統計データを解析するとき、中央値と最頻値は重要な代表値です。平均値が役に立つ場面というのは、データが正規分布になっているときに限られます。異常値（外れ値）がある場合、平均値は役に立ちません。

そのため度数分布表やヒストグラムを利用するとき、中央値と最頻値は重要です。中央値と最頻値を利用することで、データが何を意味しているのか理解できるようになるのです。

統計を学ぶとき、中央値（メジアン）と最頻値（モード）の概念を理解しましょう。また中央値や最頻値の求め方も学びましょう。