統計学ではすべての人がt分布を学ぶことになります。統計学で最も利用される方法がt分布であり、t分布を理解していない場合、多くのケースで統計処理をすることができません。
このとき、t分布を理解する前に標準正規分布やカイ二乗分布を理解している必要があります。これらの概念がわかっていない場合、t分布を学ぶことはできません。ただ理解しているのであれば、t分布を学ぶことができます。
母平均を推定する方法がt分布です。普通、母平均はわかりません。そこでt分布を利用することによって区間推定をするのです。
それでは、どのようにt分布を利用して母平均の推定をすればいいのでしょうか。ここでは、t分布を利用して母平均の95%信頼区間を計算する方法を解説していきます。
もくじ
t分布とは何か:標準正規分布とt分布の関係
まず、t分布とは何でしょうか。また、どのようなときに利用されるのでしょうか。母平均の区間推定をするとき、主に以下の2つの方法があります。
- 正規分布を用いて母平均を推定する(母分散がわかっている)
- t分布を用いて母平均を推定する(母分散がわからない)
つまり母分散がわかっている場合、標準正規分布を利用することによって母平均の95%信頼区間(または99%信頼区間)を計算できるというわけです。
ただ母平均がわからない場合、普通は母分散も不明です。母集団の平均や分散、標準偏差がわからないため、標本として小数のサンプルを集めているのです。そこで多くの場合、t分布を利用することによって、母分散がわからない状態で母平均を推定します。
正規分布とt分布の使い分けとしては、母分散(母標準偏差)がわかっているかどうかで区別しましょう。
t分布のヒストグラムと自由度によって異なるグラフの形
それでは、t分布のヒストグラムはどのような形になっているのでしょうか。正規分布とt分布のヒストグラム(グラフの形)を確認すると、以下のようになります。
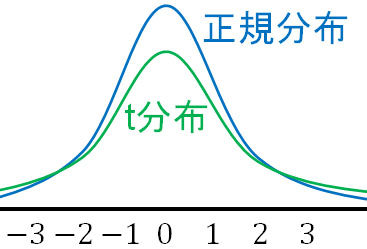
このように正規分布のほうがシャープな形となります。一方でt分布では、標準正規分布のグラフよりも少しゆるやかな曲線となります。
母分散がわかっている場合、正規分布を利用してもいいし、t分布を利用してもいいです。ただ一般的には正規分布が利用されます。この理由として正規分布のほうがグラフの形がとがっているため、より正確な95%信頼区間を出せるからです。
一方で母分散(母標準偏差)がわからない場合、正規分布を利用することができません。そこでt分布を利用するというわけです。
t分布の定義:カイ二乗分布を利用する公式
t分布はゴセットという化学者によって発見されました。彼はスチューデントというペンネームで論文を発表したため、t分布はスチューデントのt分布とも呼ばれています。
標準正規分布するデータ\(Z\)について、自由度\(n\)とカイ二乗分布\(W\)を利用し、統計量\(T\)をゴセットは以下のように定義しています。
\(T=\displaystyle\frac{Z×\sqrt{n}}{\sqrt{W}}\)
この公式をみても意味を理解できないと思います。そこでゴセットが定義したt分布について、統計量Tを以下のように考えましょう。

カイ二乗分布を利用する場合、母分散の推定が可能です。いずれにしても、標準正規分布と自由度、カイ二乗分布を利用することによってt分布を計算できると理解しましょう。
なお、なぜ統計量Tが先ほど記した定義になるのかについて、深く考えないようにしましょう。化学者であり、統計学者でもあるゴセットが考えてくれた統計量Tの計算方法が先ほど記した公式です。この公式をありがたく使わせてもらうようにしましょう。
ひとまず、自由度\(n\)とカイ二乗分布\(W\)を利用することによって、t分布を計算できることを理解すれば問題ありません。
統計量Tの公式を導く
標本を利用し、母分散の推定をするのがカイ二乗分布です。カイ二乗分布について、統計量Wと標本分散\(s^2\)、サンプル数\(n\)、母標準偏差\(σ\)を利用すると以下の式を作ることができます。
\(W×σ^2=s^2×n\)
\(W=\displaystyle\frac{s^2×n}{σ^2}\)
※なぜこの式を作ることができるのかわからない場合、カイ二乗分布を復習してみてください。
次に、標準正規分布\(Z\)を計算しましょう。標本平均を\(\overline{X}\)、母平均を\(μ\)、標本標準偏差を\(\displaystyle\frac{σ}{\sqrt{n}}\)とするとき、統計量\(Z\)は以下の公式によって計算できます。
\(Z=\displaystyle\frac{\overline{X}-μ}{\displaystyle\frac{σ}{\sqrt{n}}}\)
そこで、以下の3つを利用して式を変形しましょう。
\(T=\displaystyle\frac{Z×\sqrt{n}}{\sqrt{W}}\)
\(W=\displaystyle\frac{s^2×n}{σ^2}\)
\(Z=\displaystyle\frac{\overline{X}-μ}{\displaystyle\frac{σ}{\sqrt{n}}}\)
以下のようになります。
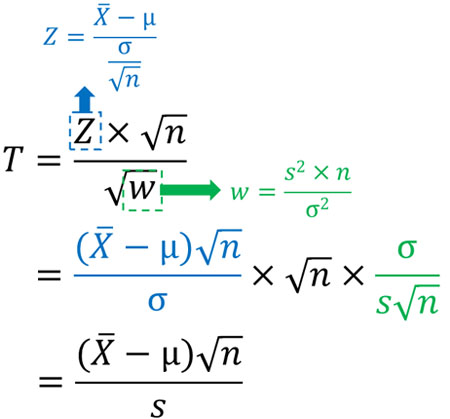
こうして、統計量Tを得るための式を変形することができました。

標本を利用すれば、標本平均や標本標準偏差を求めることができます。標本平均や標本標準偏差、サンプル数(自由度)を利用することで、母平均\(μ\)を推定できるというわけです。
t分布による区間推定:母平均の推定
それでは、実際にt分布を利用して区間推定をしてみましょう。自由度によって、データ分布が95%となる範囲が異なります。具体的には、以下のようになります。
・自由度の違いとT値の95%区間
| 自由度 | 限界値(2.5%:片側) |
| 1 | 12.706 |
| 2 | 4.303 |
| 3 | 3.182 |
| 4 | 2.776 |
| 5 | 2.571 |
| 6 | 2.447 |
| 10 | 2.229 |
| 30 | 2.042 |
例えば自由度6の場合、-2.447~2.447の間に95%のデータが含まれるようになります。図にすると以下のようになります。
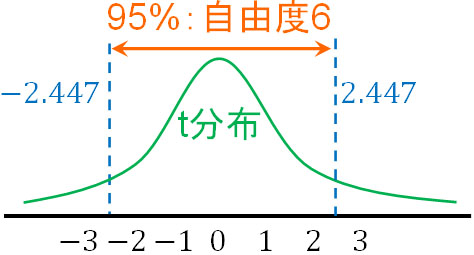
T値が2.447以上になる確率は2.5%です。またT値が-2.447以下になる確率は2.5%です。-2.447~2.447の間に95%のデータが含まれるのは、こうした理由があります。
自由度ごとに95%の範囲に収まる統計量Tが既に決まっています。そのため統計量Tを代入することによって、母平均\(μ\)の95%信頼区間を推定できるというわけです。
参考までに、自由度が240のときの統計量Tの限界値(95%)は1.970です。標準正規分布では、標準偏差に1.96にかけることによって95%信頼区間を計算します。つまり自由度(サンプル数)が大きくなると、t分布は正規分布に近づくというわけです。
t分布を利用し、母平均の推定を行う例題
それでは、実際にt分布を利用することによって母平均を推定しましょう。実際に計算をすれば、小数のサンプルを利用してどのように母平均の推定をするのか理解できるようになります。
注意点として、t分布では自由度\(n-1\)に従います。カイ二乗分布でも自由度\(n-1\)に従うことになり、これはt分布でも同様なのです。そこで母平均の推定をするとき、サンプル数から1つ引いた値を自由度に設定しましょう。
ここまでの内容を理解したうえで、以下の問題を解きましょう。
- 標本として「8、7、12、6、12」のサンプルがあります。母平均の95%信頼区間を求めましょう。
標本平均\(\overline{X}\)は9です。
\(\overline{X}=\displaystyle\frac{8+7+12+6+12}{5}=9\)
また、標本標準偏差(不偏標準偏差)\(s\)は2.83です。
\(s^2=\displaystyle\frac{1+4+9+9+9}{5-1}=8\)
\(s=\sqrt{6.4}≒2.83\)
サンプル数は5であるため、自由度は\((n-1=)4\)です。自由度4のとき、t分布での95%区間は先ほどの表より以下のようになります。
\(-2.776≦T≦2.776\)
そこで\(T=\displaystyle\frac{(\overline{X}-μ)\sqrt{n}}{s}\)へ値を代入しましょう。以下のようになります。
\(-2.776≦\displaystyle\frac{(9-μ)×\sqrt{5}}{2.83}≦2.776\)
この式を解くと以下のようになります。
\(-2.776≦\displaystyle\frac{(9-μ)×\sqrt{5}}{2.83}≦2.776\)
\(-2.776≦(9-μ)×0.79≦2.776\)
\(-3.514≦9-μ≦3.514\)
\(-12.514≦-μ≦-5.486\)
\(5.486≦μ≦12.514\)
こうして、母平均の95%信頼区間は\(5.486≦μ≦12.514\)と推定することができます。母集団が正規分布するとわかっている場合、使用するサンプル数が少ないケースであっても、t分布を利用することによって母平均の推定が可能になるのです。
また使用するデータは標本平均や標本標準偏差、自由度(サンプル数)のみです。標本を利用することによって測定できるデータを利用し、誰でも簡単に母平均の推定が可能なのがt分布の利用です。
統計学の初歩であるt分布を学ぶ
すべての統計学の教科書でt分布を学びます。t分布は統計学の初歩でもあります。ただ、多くの人が内容を理解できずに苦しんでいます。
そのためt分布を学ぶ前に、必ず標準正規分布とカイ二乗分布を理解しましょう。そうすれば、t分布を理解するのは難しくありません。このときはゴセットが考えてくれた統計量Tを出す公式を利用しましょう。そうすれば、標本平均や標本標準偏差(標本分散)を利用することで母平均の推定が可能になります。
多くの場面で区間推定が利用されます。このとき最も重要な分野がt分布です。母集団の平均や分散がわからなくても、標本を利用することで母平均の95%信頼区間(または99%信頼区間)を計算できます。
母集団が正規分布するとわかっていれば、母分散がわからず、使用する標本のサンプル数が少ないとき、t分布を利用できます。t分布の意味や正規分布との使い分け、カイ二乗分布との違いを理解して統計学を学びましょう。