ベイズ推定：ベイズ定理の公式や事前確率・事後確率の概念

多くの場面でベイズ統計学が利用されており、ベイズ定理を基本とする統計学がベイズ統計学です。ベイズ統計学ではベイズ推定の方法やベイズ定理の公式を学ぶことになります。

初めてベイズ統計学を学ぶ場合、事前確率や事後確率など新たな概念を習います。これらが何を意味しているのか理解していない場合、当然ながらベイズ推定を理解することはできません。また、ベイズ定理の公式が何を表しているのか分かりません。

ベイズ統計学は機械学習（AI）や医療など、活躍場所は多いです。特にコンピューターサイエンスでは必須の分野がベイズ統計学です。

そこでベイズ統計学の基本であるベイズ推定やベイズ定理について、どのような概念なのか解説していきます。

1 確率を面積で考える：条件によって確率が変化する
2 ベイズ推定を利用し、迷惑メール判定を行う
- 2.1 複数項目での判定：ベイズ推定での逐次合理性
- 2.2 機械学習（AI）でベイズ推定が利用される
3 ベイズ定理の公式やベイズ推定の概念を理解する

確率を面積で考える：条件によって確率が変化する

ベイズ定理を学ぶとき、確率を面積で考えることを理解しましょう。すべての確率を足すと必ず1（100%）になります。

またベイズ推定では、「条件によって確率が変化する」ことを利用します。特定の条件が発生することによって、その後の発生確率が変化するのです。まずは、これらがどのような意味をもつのか理解しましょう。

例えば、以下の場面を想定します。

トランプの中から一枚、カードを引きます。絵札を引く確率はいくらでしょうか。

トランプには1～13の数字があります。この中で絵札は11～13です。そのため絵札を引く確率は\(\displaystyle\frac{3}{13}\)であり、絵札以外のカードを引く確率は\(\displaystyle\frac{10}{13}\)です。

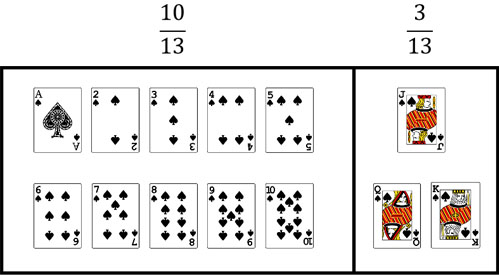
次に、もう一つ条件を加えてみましょう。「カードが3の倍数かどうか」を条件に加える場合、それぞれの確率は以下のようになります。

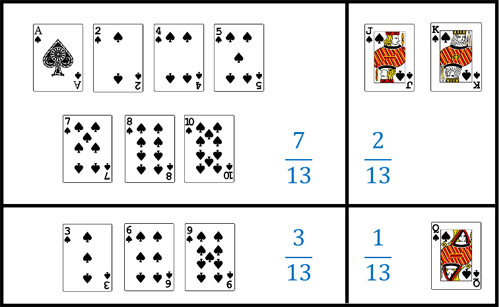
今回の場合、「絵札があるかどうか」「3の倍数かどうか」で4パターンに分けました。また、すべてを足すと1（100%）になります。いずれにしても、確率ではすべての部分（面積）を足すと必ず1になります。

観測したイベントにより確率が変わる：事後確率（ベイズ逆確率）の計算

ただ、あなたがカードを一枚引いた後、司会者から「あなたが引いたカードは3の倍数です」と伝えられたとします。この場合、当然ながら確率が変化します。

それまで、絵札を引く確率は\(\displaystyle\frac{3}{13}\)でした。しかし、あなたが引いたカードは3の倍数であると判明したため、カードが絵札である確率は以下の部分に絞られるようになります。

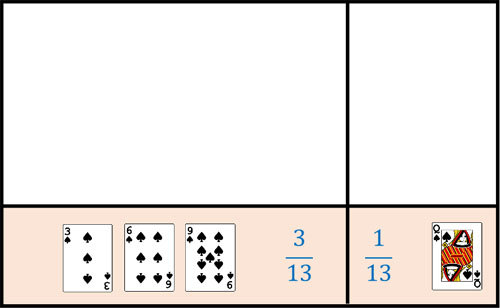
全体の確率を足すと必ず1（100%）にならなければいけません。そこで、\(\displaystyle\frac{3}{13}:\displaystyle\frac{1}{13}\)の比率のまま、2つの確率を足して1になるように変えましょう。そうすると、\(\displaystyle\frac{3}{4}:\displaystyle\frac{1}{4}\)になります。

こうして、ヒントをもらった後は絵札のカードを得られる確率が\(\displaystyle\frac{1}{4}\)へ変化しました。このように、イベント発生によって確率が変化することをベイズ更新といいます。

何かしらのイベントが起こることによって確率が変わることはよくあります。例えば病院での検査に引っかかれば、悪い病気を発症している確率が高くなります。登山家であれば、エベレストを登っているときは死亡率が高くなります。

イベント発生によって確率が変化することを私たちは日常生活の中で理解していると思います。ベイズ統計では、条件によって確率が変化する学問を取り扱います。

なおベイズ推定では、状況が変化する前の確率を事前確率といいます。一方、イベント発生後の確率を事後確率（別名：ベイズ逆確率）といいます。今回の場合であれば、カードを一枚取った段階が事前確率です。この状況に対して、ヒントをもらった後が事後確率（ベイズ逆確率）です。

条件付き確率がベイズ推定で重要：事前確率の計算

それでは、ベイズ統計学は特別な学問なのでしょうか。ベイズ推定というのは、高校数学を学んでいる人であれば、既に全員が習っています。ベイズ推定というのは、要は条件付き確率のことです。

特定の条件下にて、もう一つのイベントが起こる確率を計算するのが条件付き確率です。先ほどの例であれば、「トランプの中から一枚のカードを引くとき、3の倍数という条件下、絵札である確率」を求めました。

事前確率を計算するとなると、難しいように思えてしまいます。ただ既に条件付き確率を学習している場合、「ベイズ逆確率では条件付き確率を計算すればいい」と理解しましょう。高校数学で条件付き確率を学ぶとき、以下の公式を習ったと思います。

\(P(A|B)=\displaystyle\frac{P(A∩B)}{P(B)}\)

\(P(A|B)\)というのは、Bという条件が発生しているとき、Aという条件が起こるときの確率です。先ほどの例であれば、「A：絵札」「B：3の倍数」という条件に設定すれば、「カードが3の倍数のとき、絵札を引く確率」が\(P(A|B)\)に該当します。つまり、事後確率です。

また\(P(A∩B)\)はAかつBです。つまり「カードが3の倍数であり、かつ絵札の確率」です。つまり、確率は\(\displaystyle\frac{1}{13}\)です。また、\(P(B)\)は「カードが3の倍数である確率です。そのため、\(P(B)=\displaystyle\frac{4}{13}\)です。

そこで公式に当てはめると、\(P(A|B)=\displaystyle\frac{1}{4}\)と計算することができ、事後確率の計算が可能です。

ベイズ定理の公式を得る手順

なおベイズ推定では、事前確率と事後確率を利用します。条件付き確率では、事前確率を利用しません。そこで条件付き確率を変形することによって、ベイズ定理の公式を得ましょう。つまり事前確率を利用することによって、事後確率を得られるようにするのです。

先ほど、以下の公式が成り立つと解説しました。

\(P(A|B)=\displaystyle\frac{P(A∩B)}{P(B)}\) …①

これはつまり、事象が独立の場合、以下も成り立つことを意味します。

\(P(B|A)=\displaystyle\frac{P(A∩B)}{P(A)}\)

\(P(A|B)\)を\(P(B|A)\)に変えています。また、分母を\(P(B)\)から\(P(A)\)に変えています。\(P(B|A)\)というのは、「カードが絵札のとき、3の倍数になる確率」を指します。また、\(P(A)\)は「絵札のカードを引く確率」です。

そこで、以下のように式を変形しましょう。

\(P(B|A)=\displaystyle\frac{P(A∩B)}{P(A)}\)

\(P(A∩B)=P(B|A)P(A)\) …②

次に、②を①に代入しましょう。以下のようになります。

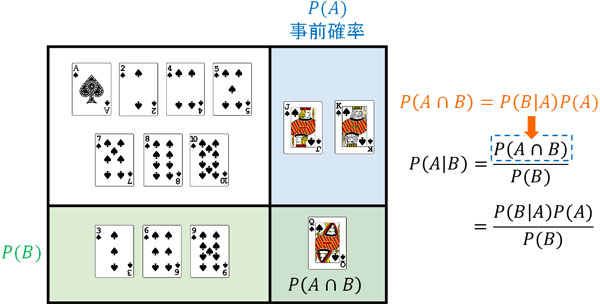
前述の通り、\(P(A|B)\)は事後確率（ベイズ逆確率）です。また、\(P(A)\)は絵札を引く確率なので事前確率です。こうして、事前確率を利用して事後確率を得る以下の公式を作ることができました。

\(P(A|B)=\displaystyle\frac{P(B|A)P(A)}{P(B)}\)

これがベイズ定理です。ベイズ定理というのは、条件付き確率の公式を変形することによって得ることができます。

またベイズ定理の公式を利用すれば、事後確率を活用することによって、事前確率を得ることもできます。先ほどの式を変形すれば、事後確率を用いて事前確率の計算が可能な式を作れるのです。

通常、統計では未来に起こる確率を予想します。一方でベイズ定理を利用すれば、現在の結果を利用して過去に起こったイベントの発生確率を予測することができます。

ベイズ推定を利用し、迷惑メール判定を行う

それでは、どのような場面でベイズ定理が利用されるのでしょうか。ベイズ推定を説明するとき、ひんぱんに利用される例として迷惑メールの判定があります。そこで、迷惑メール判定がどのように行われているのかベイズ推定を利用してやってみましょう。

私たちは多くのメールを受け取ります。その中にはスパムメールも多くあります。このとき、どのようにして迷惑メールかどうかを判断しているのでしょうか。

例えば、あなたが受け取るメールのうち70%は必要なメール、30%はスパムメールとしましょう。この場合、以下のように分けることができます。

ただ受け取ったメールのうち、どれが迷惑メールなのか判断しなければいけません。そこで、メールの中に「振込」「請求書」など、お金の支払いを要求するキーワードが含まれているかどうかに着目しましょう。

一般的なメールの場合、お金の振り込みを要求することはありません。一方でスパムメールの場合、高確率でお金の支払いを要求してきます。そこで、「メール内にお金の要求がある場合（または、ない場合）」という条件を設定するとき、スパムメールかどうかの確率が以下のようになるとします。

	お金の要求あり	お金の要求なし
必要なメール	20%	80%
迷惑メール	90%	10%

この場合、以下の4つに分けることができます。

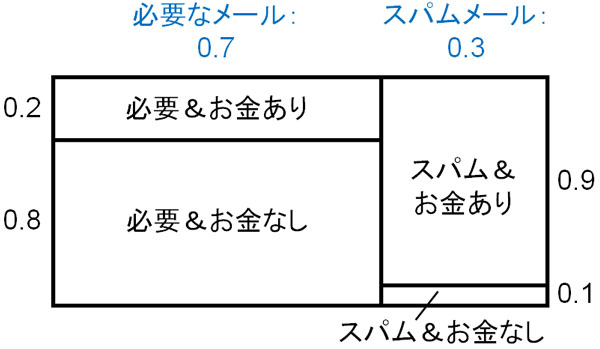
それでは、メール内にお金に関する内容が含まれていると判明しました。この場合、お金なしの内容が消えます。そのため、以下部分にのみ着目しましょう。

必要なメールであり、かつお金の要求ありの場合、面積は\(0.7×0.2=0.14\)です。一方、スパムメールであり、かつお金の要求がある場合、面積は\(0.3×0.9=0.27\)です。

そこで\(0.14:0.27\)について、同じ比率のまま面積が1になるように調節しましょう。そうすると、\(\displaystyle\frac{14}{41}:\displaystyle\frac{27}{41}\)になります。つまり、お金の要求があるという条件では、スパムメールの確率は\(\displaystyle\frac{27}{41}≒65.9\)%です。

次に、ベイズ定理の公式を利用して同じ答えを出してみましょう。ここまで説明した通り、ベイズ推定では公式を利用しなくても事後確率（または事前確率）の計算が可能です。ただ公式を習ったため、公式を利用できるようにするのです。

\(P(A)\)を迷惑メールの確率、\(P(B)\)をお金の要求がある確率とすると、以下のようになります。

\(P(A)=0.3\)

\(P(B)=0.7×0.2+0.3×0.9=0.41\)

\(P(B|A)=0.9\)：※迷惑メールのうち、お金の要求がある確率

これらの情報は既にわかっています。そこで、「お金の要求がある中で、迷惑メールである確率\(P(A|B)\)」を先ほどの公式に代入することで計算してみましょう。

\(P(A|B)=\displaystyle\frac{P(B|A)P(A)}{P(B)}\)

\(=\displaystyle\frac{0.9×0.3}{0.41}\)

\(=\displaystyle\frac{27}{41}\)

こうして、図を用いて解説したケースと同じ答えを得ることができました。ベイズ定理の公式をみても、意味を理解することはできません。そこで図を利用し、事前確率や事後確率の意味を学び、イベント発生によってどのように確率が変化するのか理解しましょう。

複数項目での判定：ベイズ推定での逐次合理性

ただ迷惑メールの判定をするとはいっても、1つの項目で判断してはいけません。ビジネスメールのやり取りでは、請求書の送付を含めお金の振り込みを依頼する場面は非常に多いです。そうした重要なメールについて、お金の支払いに関する内容が含まれていることによってスパムメールと判定されるのは不都合です。

そのため実際には、より多くの項目を設定することでスパムメールかどうかを判定します。次に、「お金の要求がある」ことに加えて、URLが貼ってあるかどうかを基準に加えましょう。

この場合、要素は3つになります。そのため、図は8つに分割されます。例えば以下のケースを考えてみましょう。

・お金の要求ありのケース

	URLあり	URLなし
必要なメール	40%	60%
迷惑メール	80%	20%

・お金の要求なしのケース

	URLあり	URLなし
必要なメール	50%	50%
迷惑メール	70%	30%

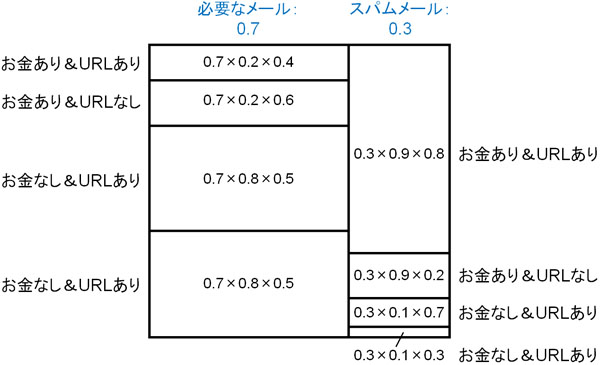
このように、項目が増えるとより細分化されます。またお金の要求があり、かつURLがメール内に存在する場合だと、スパムメールである確率が高くなります。こうして複数の項目を利用して判断し、ある一定水準を超えると「このメールは迷惑メールである」とコンピューターが判断します。

・ベイズ推定で重要な逐次合理性

ただ複数の項目について、細かく分けると図が非常に複雑になります。3つの要素であれば先ほど示した通り、図を8つに分けることができます。ただ実際には多くの要素を考慮する必要があるため、細かく分けて判断するのは大変です。

そこで、ベイズ推定の特徴である逐次合理性を利用しましょう。ベイズ推定には、「以前の試行を忘れる」という性質（逐次合理性）があります。

例えば先ほど、お金の要求があるケースについて、スパムメールかどうかの確率を計算しました。このとき、以下のように事後確率を全体で1（100%）になるように調節しました。

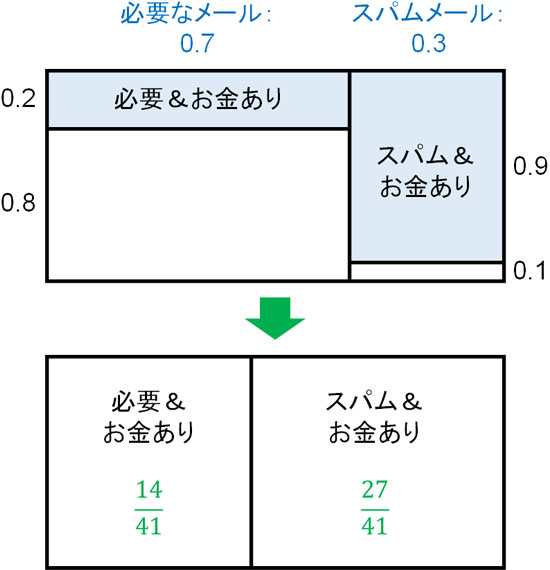
そこで「お金の要求があるケースでの事後確率」を計算したあと、次はこの確率を事前確率に変えましょう。つまり「スパム＆お金の要求ありの確率\(P(A)\)」を事前確率に設定し、「URLが存在するケースについて、スパム＆お金の要求ありの確率\(P(A|B)\)」を事後確率に設定するのです。

この場合、以下のような図になります。

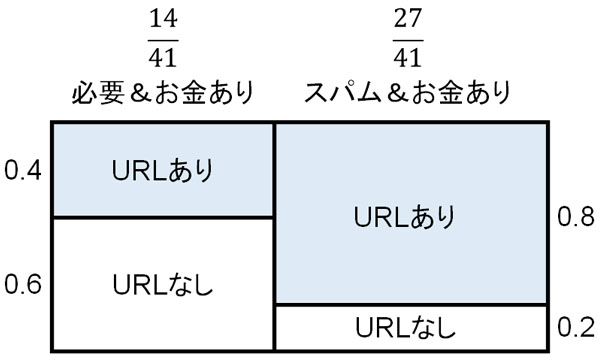
そこで先ほどと同じように「必要なメール＆お金の要求あり＆URLありのケース」と「スパムメール＆お金の要求あり＆URLありのケース」の面積を確認し、2つを合計して1（100%）になるように調節しましょう。

そうすると、「URLありのとき、スパムメール＆お金の要求ありの確率」は\(\displaystyle\frac{27}{34}≒0.794\)になります。

またベイズ定理の公式を利用する場合、\(P(A)\)を「スパムメール＆お金の要求ありの確率」、\(P(B)\)を「URLありの確率」とすると、以下のようになります。

\(P(A)=\displaystyle\frac{27}{41}\)

\(P(B)=\displaystyle\frac{14}{41}×0.4\)\(+\displaystyle\frac{27}{41}×0.8\)\(=\displaystyle\frac{136}{205}\)

\(P(B|A)=0.8\)：※スパムメール＆お金の要求ありのうち、URLありの確率

そこでベイズ定理の公式に代入しましょう。

\(P(A|B)=\displaystyle\frac{P(B|A)P(A)}{P(B)}\)

\(=\displaystyle\frac{0.8×\displaystyle\frac{27}{41}}{\displaystyle\frac{136}{205}}\)

\(=\displaystyle\frac{27}{34}\)

こうして、ベイズ定理の公式を利用する場合であっても「URLありのとき、スパムメール＆お金の要求ありの確率\(P(A|B)\)」は\(\displaystyle\frac{27}{34}≒0.794\)になると計算できました。2つの要素を組み合わせて判定する場合、0.784（79.4%）の確率であるため、迷惑メールを正しく判定できるようになります。

もちろん79.4%の確率ではスパム認定の基準値として低いため、さらにほかの要素を加えることによって細かく条件分けをしていく必要があります。

なお重要なのは、事後確率を事前確率に設定して次の計算をしてもいいことです。逐次合理性を利用することにより、多くの要素を加えるにしても、一つずつ順に計算できます。そのため、計算過程は簡単になります。

機械学習（AI）でベイズ推定が利用される

特にコンピューターサイエンスでベイズ定理が重要な理由としては、機械学習（AI）でベイズ推定が用いられているからです。

イベント発生によって確率が変化するとき、どのようなパターンであれば正確に判断できるのかについて、ベイズ推定を用いてAIが学習するのです。先ほどの例であれば「メール内にお金に関するキーワードがあったり、URLが含まれていたりする場合、迷惑メールの可能性が高い」と判断するのです。

そのため機械学習では、事前に多くの条件を用意しておきます。それと同時に、正解と不正解（今回の例であれば、迷惑メールかどうか）を用意します。そこで、さまざまなパターンについて「どのようなケースであれば正解なのか（または不正解なのか）」を学習させるのです。

またAIというのは、多くの人に利用されるほど精度が高くなります。あなたもメールを受け取ったとき、本当は必要なメールであるにも関わらず、相手からの連絡で「実は迷惑メールに入っていた」ことが判明した経験はあると思います。

この場合、あなたは迷惑メールボックスの中から必要なメールを探し、そのメールに対して受信ボックスに戻し、「スパムではない」など何らかのアクションを起こすことになります。そうすると、AIは「この内容のメールは必要なメールであり、スパムメールではない」と学び、新たな条件を加えるようになります。こうして、ケーススタディーが多くなるほどAIの精度は高まります。

人間というのは、失敗を繰り返すことによって「何をすれば正解を得ることができるのか」を学びます。AIの場合、ベイズ推定を利用すれば人間と同じように失敗から成功を学べるようになります。これが、コンピューターサイエンスでベイズ統計学が重要な理由です。