統計学に限らず、多くの場面で加重平均という言葉が利用されます。非常に重要な概念であり、発表される統計データのほとんどは加重平均を加味していると理解しましょう。
それでは、なぜ加重平均が重要なのでしょうか。この理由として、単なる平均値では実情を反映できないからです。そこでデータを加重平均へ直し、実情に合わせた値に変換する必要があるのです。そこで、加重平均の意味や計算方法を理解しましょう。
このとき、一般的な平均(単純平均)と加重平均は何が違うのでしょうか。また、加重平均の求め方には何があるのでしょうか。
仕事や投資、学術論文など多くの場面で加重平均が利用されます。そこで、加重平均の意味や公式、計算方法を解説していきます。
もくじ
単純平均とは異なる加重平均の意味
私たちにとって平均という言葉にはなじみがあります。小学算数で学ぶのが平均です。それでは、単純平均と加重平均は何が違うのでしょうか。
まず、平均値とは「全体をならす場合の値」を表します。例えばテストを行い、Aさんが60点であり、Bさんが80点の場合、平均値は70点です。
次に一人の点数ではなく、グループの点数を考えてみましょう。例えばAグループの平均点数が60点であり、Bグループの平均点数が80点だったとします。この場合、一人あたりの平均点はいくらでしょうか。
答えは「わからない」が正解です。グループの人数が明確ではないからです。先ほどとは異なり、全体の平均点は必ずしも70点とは限りません。例えばグループAが1人、グループBが19人の場合、平均点は79です。

\(\displaystyle\frac{1×60+19×80}{20}=79\)
グループによって人数が異なる場合、それぞれの重要度(今回の場合はグループに含まれている人数)を考慮しなければいけません。単純に値を足し、グループ数で割っても正確な平均値を出すことはできないのです。
グループ単位での平均(単純平均)であれば、なにも考えずに平均値を出せばいいです。一方、一人あたりの平均だとグループに含まれる人数が重要になります。
このように、重要度を加味して計算しなければいけないケースは多いです。加重平均では、重要度を考慮して現実的な平均値を得ることができます。
それぞれのグループを一つの集団に戻して平均を計算する
加重平均の求め方として、最もわかりやすい例としては、グループを一つにまとめてしまうことがあげられます。
例えば3つのグループがある場合、それぞれのグループの平均値を利用しても、全体の平均(加重平均)を計算することはできません。得られるのは単純平均です。そこで、それぞれのグループに個数がいくつ含まれているのかを確認して計算した後、全体の個数で割りましょう。
例えばテストの点数について、以下のケースを考えてみましょう。
- グループA:平均50点(10人)
- グループB:平均60点(5人)
- グループC:平均70点(15人)
この場合、グループごとに合計点数を計算しましょう。その後、全体の人数(30人)で割ります。つまり、以下のようになります。
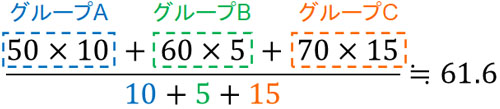
このようにして、それぞれのグループを一つの集団にまとめてしまえば加重平均を計算できるようになります。
それぞれの重要度を加味して加重平均を計算する
ただ実際のところ、先ほど解説した「グループを一つの集団にまとめる」ことができないケースは多いです。性質が同じでない場合、一つの集団にまとめることはできません。例えばインフレ率(生活費の値上がり率)を計算するとき、以下の要素などを考慮してインフレ率の計算をします。
- 住宅価格(家賃)
- 食費
- エネルギー価格
- 輸送費(交通費)
このように性質がまったく異なる要素については、どのように加重平均を計算すればいいのでしょか。この場合、要素ごとに比率(重み)をつけましょう。このような比重(比率)を利用する方法であれば、すべてのパターンについて加重平均を計算できます。
例えば日常生活でのあらゆる支出の中でも、最も負担が大きいのは居住費です。家賃が高いのは当然として、持ち家であっても住宅ローンの支払いが必要です。そのため通常、インフレ率を計算するときは「住宅価格がどれだけ上昇したのか」が最も大きな影響を与えます。
一方、交通費の値段が上がっても生活費への影響は少ないです。多少は影響があるものの、住宅費の高騰に比べると影響は小さいのです。そこで、例えば以下のような比率とします。
- 住宅価格:0.6(60%)
- 食費:0.2(20%)
- エネルギー:0.1(10%)
- 輸送費(交通費):0.1(10%)
このとき、住宅価格と食費の2つを加味したインフレ率はどのように計算すればいいでしょうか。加重平均を利用する場合、以下のように計算します。

加重平均というのは、要は「重要度を加味して計算する方法」です。重要度というのは、比率によって表されます。今回の例では、住宅価格が日々の支払いに大きく関与しているため、重要度が高いというわけです。
加重平均を出すときの公式
ここまでの内容を理解したうえで、加重平均を出すときの公式を学びましょう。例えば3つのグループ(\(x_1,x_2,x_3\))について、それぞれの重要度(重み)を\(w_1,w_2,w_3\)とします。
この場合、加重平均は以下のようになります。
- \(\displaystyle\frac{x_1w_1+x_2w_2+x_3w_3}{w_1+w_2+w_3}\)
加重平均を学ぶとき、最初に公式をみても意味を理解できません。ただ先に例題を学べば、この公式がもつ意味を理解できると思います。
なお先ほど解説した通り、加重平均の求め方には2つの方法があります。ただ用いる公式は同じなので、どちらの計算方法を利用しても問題ありません。
単純平均より、加重平均のほうが現実的な値となる
最もシンプルな平均の計算方法は単純平均です。私たちが最初に学ぶ平均の概念が単純平均です。通常、平均値は単純平均で計算した値を指します。
一方、重要度を加味した平均値が加重平均による値です。実際のところ、単純平均では実情を反映できていないケースが多いです。そこで加重平均を利用するのです。
単純平均よりも、加重平均で計算したほうが現実的な値となります。加重平均が仕事や投資、学術論文でひんぱんに利用される理由は、単純平均よりも加重平均のほうが正確だからです。
多くの人は単純平均を利用するものの、実際のところ正確な値ではないケースが多いです。そこで加重平均を利用すれば、正確な値を提示できるようになります。
加重平均の意味と計算方法を学ぶのは重要
加重平均は私たちにとってなじみのない言葉です。ただ実際には、多くの場面で加重平均が利用されています。単純平均を利用しても正確でない場面は多いのです。
グループによって重要度が異なることはよくあります。その場合、加重平均を利用しましょう。グループごとに異なる重みを加え、計算するのです。
なお加重平均を学ぶとき、公式をみても意味を理解できません。そこで、最初は必ず例題を確認しましょう。加重平均には2つの計算方法があり、両方のやり方を学ぶのです。そのあとに公式をみれば、公式がどのような意味をもつのか理解できるようになります。
仕事や投資を含め、さまざまな場面で加重平均は役立ちます。また実際のところ、公表されている統計データの多くは加重平均です。そこで加重平均の概念を理解し、加重平均を利用して計算できるようになりましょう。