中学数学で学ばなければいけない分野が二次方程式です。一次方程式に比べて、複雑な計算になるのが二次方程式です。
二次方程式では、答えを出す方法が複数あります。解答の方法としては、平方根や因数分解、解の公式が代表的な方法です。二次方程式を解くとき、どの方法によって答えを出せばいいのか区別しなければいけません。これが、一次方程式に比べて難しくなりやすい理由です。
平方根や因数分解など、これまで習ってきたことを利用することで二次方程式の答えを出すことができます。また文章題の二次方程式も頻繁に出されるため、方程式を作れるようにしなければいけません。
どのように二次方程式の問題を解けばいいのかについて、答えの出し方だけでなく、文章題の解き方まで含めて解説していきます。
もくじ
\(x^2\)の方程式が二次方程式
まず、二次方程式とは何なのでしょうか。2つの式をイコールでつなぐ式が方程式です。方程式の中でも、式の中に\(x^2\)が存在する場合、二次方程式と呼ばれます。
そのため、以下はすべて2二次方程式です。
- \(x^2=9\)
- \(x^2+4x+3=0\)
- \((x+5)^2=36\)
共通点として、式の中に\(x^2\)があります。こうした式が二次方程式です。一次方程式と二次方程式では、大きく異なる点があります。それは、二次方程式では答えが2つあることです。例えば、以下の二次方程式の答えは何でしょうか。
- \(x^2=16\)
2乗することで16になる数字としては、4があります。42は16です。そのため、\(x=4\)が答えです。ただ、-4を2乗しても16になります。(-4)2の答えは16です。そのため、\(x=-4\)も答えです。
二次方程式では、答えが1つとは限らず、2つ存在することもあることを理解しましょう。答えが1つのときがあれば、2つのときもあるのです。これが、一次方程式と二次方程式の大きな違いです。
二次方程式は3つの解き方がある
なお中学数学で学ぶ二次方程式では、解き方が3つあります。具体的には、以下の3つになります。
- 平方根を利用する
- 因数分解を利用する
- 解の公式を利用する
この方法のうち、どれかを利用して答えを出します。二次方程式によって答えの出し方が異なるため、どの方法が最適なのか見分けられるようにしましょう。
平方根を利用して二次方程式を解く
二次方程式の答えを出すとき、平方根を利用して解く方法があります。平方根を利用できる場面は限られます。ただ利用できる場合、平方根によって簡単に答えを出すことができます。
平方根で答えを出す場合、以下のような二次方程式の形になっている必要があります。
- \(ax^2=b\)
- \((x+a)^2=b\)
二乗の式をイコールでつなぐことができる場合、平方根を利用できます。答えの出し方としては、根号(ルート)を付けるだけです。以下のように、ルートを付ければ二乗を消すことができます。
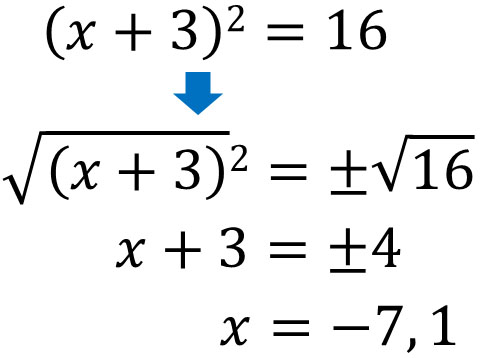
二次方程式の問題を解くとき、最も簡単に答えを出せる方法が平方根の利用です。根号を付けるだけで、二次方程式の答えを出せます。
左辺を因数分解して、右辺を0にする
二次方程式で答えを出すとき、頻繁に利用される方法が因数分解です。乗法公式を利用することで、答えを出すのです。
乗法公式には以下の4つがあります。
- \((x+a)(x+b)=x^2+(a+b)x+ab\)
- \((x+a)^2=x^2+2ax+a^2\)
- \((x-a)^2=x^2-2ax+a^2\)
- \((x+a)(x-a)=x^2-a^2\)
この公式を覚えていない場合、因数分解することができません。つまり、二次方程式の問題を解くことができません。乗法公式を覚えるのは、数学の問題を解くために必須の知識です。
それでは、どのように因数分解すればいいのでしょうか。因数分解によって二次方程式の答えを出す場合、必ず\(a=0\)の形にしましょう。必ず右辺はゼロでなければいけません。例えば、以下の二次方程式の答えは何でしょうか。
- \(x^2+6x+5=0\)
最初、この式を因数分解しましょう。乗法公式を利用すると、以下の式に因数分解できます。
- \((x+1)(x+5)=0\)
この二次方程式を満たす\(x\)の数字を答える必要があります。\(x\)にどのような数字を代入すれば、右辺がゼロになるでしょうか。
数学では、どのような数字であっても「ゼロを掛けると、答えがゼロになる」という性質があります。そこで、\((x+1)\)または\((x+5)\)が0であれば、右辺が0になると分かります。
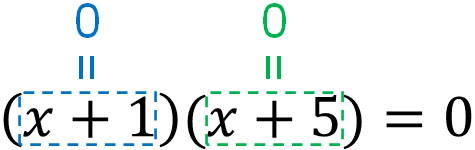
\((x+1)\)または\((x+5)\)が0になる\(x\)としては、-1と-5です。つまり、\(x=-1,x=-5\)が正解です。このように右辺を0にした後、左辺を因数分解します。そうすれば、二次方程式の答えを出せます。
二次方程式の解の公式によって複雑な答えを求める
ただ、場合によっては複雑な答えになることがあります。
平方根を使う場合、2乗の式にしなければいけません。因数分解を利用する場合、左辺の因数分解ができなければいけません。それでは、平方根も因数分解も利用できない二次方程式の場合はどのようにして答えを出せばいいのでしょうか。
この場合、二次方程式の解の公式を利用します。二次方程式の答えを出す公式が存在します。これを解の公式と呼びます。\(ax^2+bx+c=0\)のとき、\(x\)の答えを出す公式が解の公式です。二次方程式の解の公式は以下になります。
$$x={-b\pm\sqrt{b^2-4ac}\over2a}$$
かなり複雑な公式ですが、これが解の公式です。二次方程式を確認して、数字を解の公式に代入することで答えを出すことができます。
例えば、以下の二次方程式があるとします。
- \(2x^2+3x-4=0\)
この二次方程式の答えを出したい場合、解の公式へ以下のように代入します。
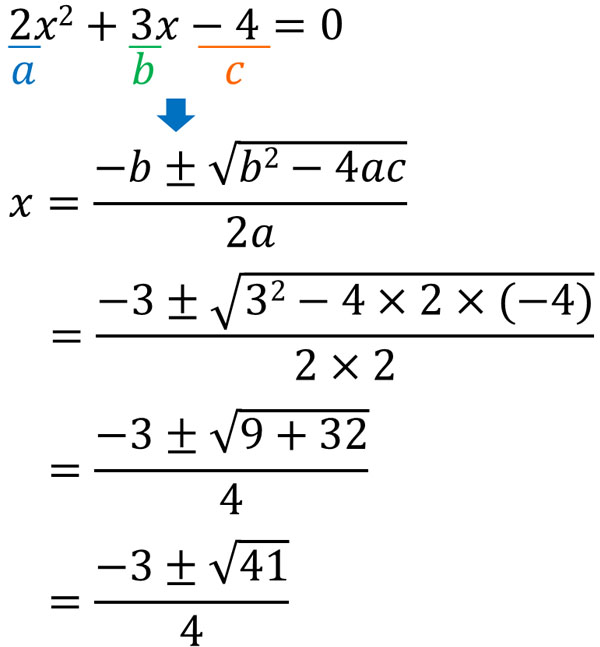
平方根や因数分解を利用できなかったとしても、解の公式を利用すれば答えを出すことができます。解の公式は覚えなければいけないものの、計算問題で答えを出せます。
なぜ、二次方程式の解の公式が成立するのかについては、これまでの数学の知識を使って説明することが可能です。
ただ証明するときの計算式は複雑です。また、解の公式を利用して答えを出すとき、毎回公式の証明をする人はいません。そのため、なぜ解の公式が成り立つのか説明するのは省略します。二次方程式の解の公式は覚えてしまいましょう。
\(b\)が偶数のときは簡略化した解の公式を使う
なお、解の公式を利用して問題を解く場合、\(b\)が偶数の場合は簡略化した解の公式を利用するのが一般的です。
偶数の場合、必ず2で割ることができます。そこで、2で割ったあとの\(b\)を\(b’\)とします。つまり、\(b’=\displaystyle\frac{b}{2}\)です。その場合、以下の解の公式が成り立ちます。
$$x={-b’\pm\sqrt{b’^2-ac}\over a}$$
二次方程式の解の公式と同じなので、絶対にこの公式を覚えなければいけないというわけではありません。ただ、数学で問題を解くとき覚えておくことをおすすめします。その方が計算速度は速くなり、さらには計算ミスを防げるからです。
例えば、以下の二次方程式について解の公式を使って解いてみましょう。
- \(2x^2+4x-1=0\)
それぞれの解き方を比較すると、以下のようになります。
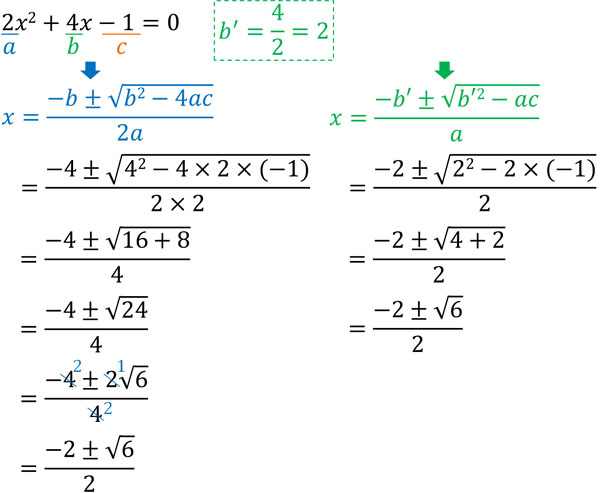
どちらも同じ答えになります。ただ、簡略化した解の公式を利用しない場合、計算が複雑になります。素因数分解をすることで、ルート内の数字を小さくしなければいけません。また約分することで、分数の数字を小さくする必要があります。
数学では、数字が大きくなり、手順が多くなるほど計算ミスが起こりやすくなります。計算ミスを防ぐため、二次方程式の答えを出すとき、ほとんどの人が簡略化した解の公式を利用します。
2次方程式の文章題の解き方
このようにして、3つの解き方の中からどの方法が最適なのか見極めるようにしましょう。
なお数学では、実生活の中で活用することが最も重要です。計算できるだけでなく、実際に利用しなければいけません。そのため、文章題を解けるようにする必要があります。文章題の解き方としては、一次方程式や連立方程式と同じです。以下のようなステップになります。
- 分からない数を\(x\)にする
- 問題文から二次方程式を作る
- 二次方程式を解く
これまで、数学で文章題を解いている場合、二次方程式の文章題もやり方は同じです。
答えが最適かどうか必ず確認する
ただ二次方程式の場合、注意しなければいけないことがあります。それは、答えが最適かどうか必ず確認しなければいけないという点です。
前述の通り、二次方程式では2つの答えが出てくることがよくあります。そのとき、一方の答えは最適ではないことがよくあります。数字としては答えがあるものの、現実世界ではあり得ないことがよくあるのです。
例えば、以下の二次方程式を解いてみましょう。
- たて\(x\)cm、横\((x-2)\)cmの長方形の面積は24cm2です
長方形の面積は「たて×横」の公式によって出すことができます。そのため、以下の二次方程式を作ることができます。
- \(x(x-2)=24\)
この二次方程式を解くと、以下のようになります。
\(x(x-2)=24\)
\(x^2-2x=24\)
\(x^2-2x-24=0\) (因数分解をする)
\((x-6)(x+4)=0\)
\(x=-4,x=6\)
この通り、二次方程式を解くことで2つの答えが出てきます。ただ、\(x=-4\)は答えではありません。\(x=-4\)の場合、\(x(x-2)=24\)の方程式を満たします。しかし、現実世界で長方形のたての長さが-4cmになることはありません。そのため、答えは6cmだけです。
温度の問題であれば、答えがマイナスになってもいいです。現実世界では、温度がマイナスになるのは普通です。ただ、長方形のたてや横の長さがマイナスになってはいけません。
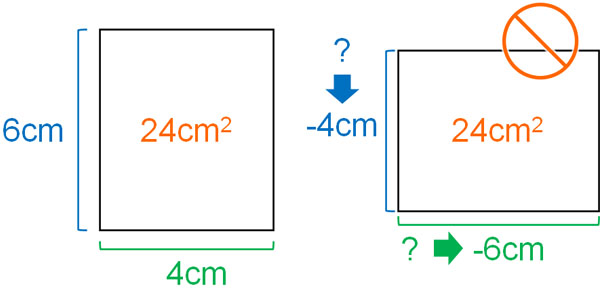
二次方程式の文章題で注意しなければいけないのは、出てきた答えが必ずしも正解とは限らないことです。\(x\)の答えを出したとしても、答えが適しているかどうか必ず確認しましょう。
練習問題:二次方程式の計算と文章題
Q1. 次の二次方程式を解きましょう
- \(2x^2-12=0\)
- \((x+2)(x+4)=24\)
- \(x^2+5x+2=0\)
A1. 解答
二次方程式の解き方としては、3つの方法があります。どの方法が最適なのか確認して問題を解くようにしましょう。
(a)
平方根を利用して解きます。
\(2x^2-12=0\)
\(2x^2=12\)
\(x^2=6\)
\(x=\sqrt{6},x=-\sqrt{6}\)
(b)
因数分解を利用して解きます。
\((x+2)(x+4)=24\)
\(x^2+6x+8=24\)
\(x^2+6x-16=0\)
\((x+8)(x-2)=0\)
\(x=2,x=-8\)
(c)
解の公式を利用して解きます。
\(x^2+5x+2=0\)
\(\displaystyle x={-5\pm\sqrt{5^2-4×1×2}\over 2×1}\)
\(\displaystyle x={-5\pm\sqrt{25-8}\over 2}\)
\(\displaystyle x={-5\pm\sqrt{17}\over 2}\)
Q2. 次の文章題を解きましょう
横がたてより4m長い長方形の土地があります。この土地に幅1mの道を作り、以下のように4つの花だんを作ります。

花だんの面積の合計が45m2の場合、たての長さはいくらでしょうか。
A2. 解答
例えば建築設計の仕事をする場合、このような計算をしなければいけません。数学は実際に活用することに意味があり、二次関数が多くの場面で利用されます。
この文章題を解くとき、図の中に数字を書き込みしましょう。そうしなければ問題を解くことは難しいです。土地のたての長さを\(x\)mとすると、以下のようになります。
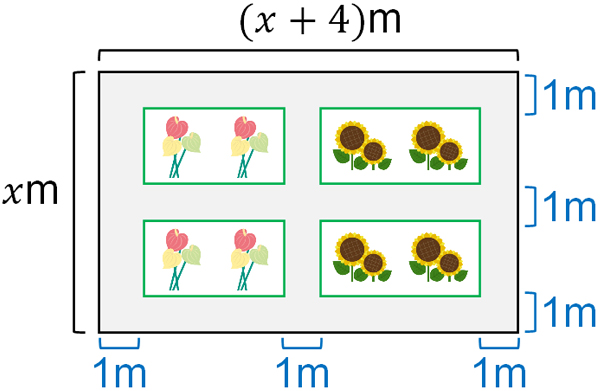
また、4つの花だんがバラバラに存在すると分かりにくいです。そこで、仮にすべての花だんを左上に移動させます。
花だんの面積の合計は変わりません。つまり、花だんを移動させても答えの数字は変わりません。実際に花だんを作るとき、元の状態に戻せばいいです。そこで仮に移動させた状態を考えて、二次方程式の式を作りましょう。そうすると、以下のようになります。
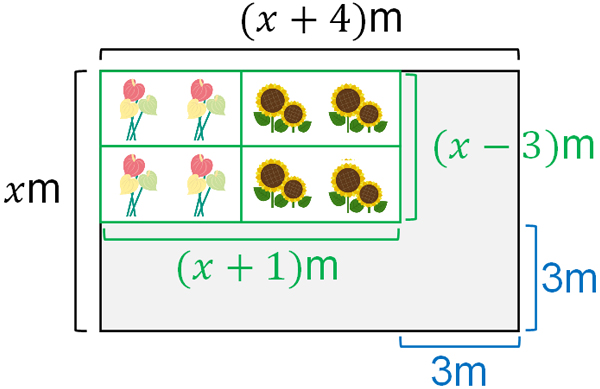
1つの道の幅は1mなので、3つの道の幅の合計は3mです。そのため、花だんのたての長さの合計は\((x-3)\)mです。また、花だんの横の長さの合計は\((x+1)\)mです。
花だんの面積の合計は45m2なので、以下の二次方程式を作ることができます。
- \((x-3)(x+1)=45\)
この二次方程式を解きましょう。
\((x-3)(x+1)=45\)
\(x^2-2x-3=45\)
\(x^2-2x-3-45=0\)
\(x^2-2x-48=0\)
\((x-8)(x+6)=0\)
\(x=8,x=-6\)
二次方程式を解くことで、\(x=8,x=-6\)と答えが出ました。しかし、土地のたての長さが-6mになることはありません。数字は正の数でなければいけません。そのため-6mは答えとして不適であり、除外する必要があります。そのため、土地のたての長さは8mとなるのが正解です。
数学の問題では、問題文の図を見ても解くのが非常に難しいケースがよくあります。ただ、今回の練習問題のように、図を移動させることで問題が簡単になり、二次方程式を作れるようになることがよくあります。
数字が合っていれば、図を自由に変形させて問題ありません。どのように図を変えれば、計算しやすくなるのか考えるようにしましょう。
二次方程式の計算問題を解く
\(x^2\)をもつ式が二次方程式です。数学で二次方程式の問題を解く場合、難易度が上がります。それまで学んできた複数の知識を利用しなければいけないからです。
二次方程式の問題を解く場合、以下を理解していなければいけません。
- 平方根
- 因数分解
また、二次方程式の解の公式を覚える必要があります。このように二次方程式には3つの解き方があり、どのやり方が最適なのか見分けなければいけません。さらには、解の公式は2種類あるため、両方を利用できるようにしておきましょう
それに加えて二次方程式の文章題では、解答した答えの一方が不適なことがあります。一次方程式に比べて注意点が多く、問題の解き方が複雑になるのが二次方程式です。どのように二次方程式を解けばいいのか理解しましょう。






