空間ベクトル：空間座標、ベクトルの分解、距離、平行条件

ベクトルを学ぶとき、私たちが最初に習うのは平面ベクトルです。平面ベクトルでは、\(x\)軸と\(y\)軸の2つを考えればいいです。一方で空間ベクトルでは立体になるため、\(x\)軸と\(y\)軸に加えて\(z\)軸を考慮しなければいけません。

ただ平面ベクトルを理解している場合、空間ベクトルは難しくありません。ベクトルの概念は同じですし、利用する公式もほぼ同じです。当然、計算方法も違いはありません。

つまり、平面ベクトルと空間ベクトルはほぼ同じ概念と考えましょう。これが、平面ベクトルを理解していれば空間ベクトルを容易に理解できる理由です。

それでは、立体図形でのベクトルはどのように考えればいいのでしょうか。空間座標や2点間の距離、空間ベクトルの分解、平行条件、ベクトルの大きさの最小値について解説していきます。

1 空間座標と平面ベクトルとの違い
- 1.1 空間ベクトルの計算は平面ベクトルと同じ
2 空間ベクトルの分解と成分表示
- 2.1 平行条件と空間ベクトル
- 2.2 2点間の距離とベクトルの大きさの最小値
3 空間ベクトルの基本を理解する

空間座標と平面ベクトルとの違い

平面ベクトルでは、\(x\)軸と\(y\)軸の2方向を考えます。つまり、二次元でベクトルを計算します。一方、空間ベクトルでは\(x\)軸、\(y\)軸、\(z\)軸の3方向で考えます。つまり、三次元で計算するのが空間ベクトルです。

三次元であるため、特定の点Pを表すとき、空間ベクトルでの位置ベクトルは\(\overrightarrow{p}=(x,y,z)\)となります。そのため、平面ベクトルで表す位置ベクトル\(\overrightarrow{p}=(x,y)\)に比べて、記すべき座標が一つ増えます。

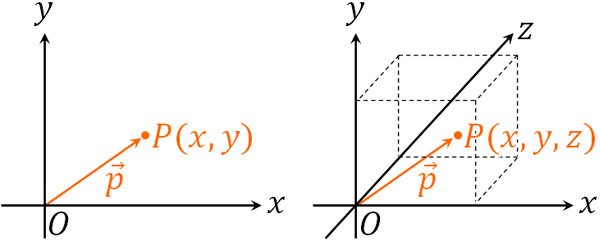
なお一般的には、点Aの位置ベクトルを\(\overrightarrow{a}=(a_1,a_2,a_3)\)と記します。\(x\)成分が\(a_1\)、\(y\)成分が\(a_2\)、\(z\)成分が\(a_3\)です。

空間ベクトルの計算は平面ベクトルと同じ

前述の通り、空間ベクトルの計算は平面ベクトルとほぼ同じです。平面ベクトルで利用できる計算法は空間ベクトルでも利用できます。そのため、空間ベクトルでは以下のように計算しましょう。

交換法則：\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\)
結合法則：\((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\)\(=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\)
ゼロベクトル：\(\overrightarrow{AA}=\overrightarrow{0}=|\overrightarrow{0}|\)
逆ベクトル：\(\overrightarrow{a}-\overrightarrow{a}=\overrightarrow{0}\)
0の性質：\(\overrightarrow{a}-\overrightarrow{0}=\overrightarrow{a}\)
実数倍：\(k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{b}+k\overrightarrow{a}\)
実数倍：\((k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}\)
実数倍：\(k(l\overrightarrow{a})=kl\overrightarrow{a}\)

足し算や引き算、実数倍をするとき、やり方は平面ベクトルも空間ベクトルも同じです。

空間ベクトルの分解と成分表示

それでは、空間ベクトルで成分表示をしましょう。足し算や引き算、実数倍をするとき、成分ごとに行う必要があります。例えば点A：\(\overrightarrow{a}=(a_1,a_2,a_3)\)と点B：\(\overrightarrow{b}=(b_1,b_2,b_3)\)があるとき、足し算は以下のようになります。

\(x\)成分：\(a_1+b_1\)
\(y\)成分：\(a_2+b_2\)
\(z\)成分：\(a_3+b_3\)

また、引き算は以下になります。

\(x\)成分：\(a_1-b_1\)
\(y\)成分：\(a_2-b_2\)
\(z\)成分：\(a_3-b_3\)

\(\overrightarrow{a}\)を実数倍（\(k\)）する場合であれば、以下のようになります。

\(x\)成分：\(ka_1\)
\(y\)成分：\(ka_2\)
\(z\)成分：\(ka_3\)

これらの計算は平面ベクトルとほぼ同じであるため、容易に理解できると思います。

・空間ベクトルの分解

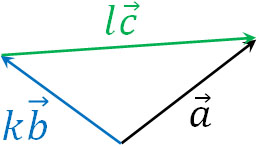
なお、1つのベクトルは分解することができます。平面ベクトルであれば、2つのベクトルを利用して1つのベクトルを表現できます。例えば、以下のベクトルがあるとします。

この場合、2つのベクトルを実数倍した後、つなぐことによって1つのベクトルを作ることができます。上図であれば\(\overrightarrow{b}\)を\(k\)倍、\(\overrightarrow{c}\)を\(l\)倍することで\(\overrightarrow{a}\)を作れます。

\(\overrightarrow{a}=k\overrightarrow{b}+l\overrightarrow{c}\)

一方、空間ベクトルでは\(x\)成分、\(y\)成分、\(z\)成分の3つを考慮しなければいけません。そこで空間ベクトルでは2つのベクトルではなく、3つのベクトルを利用して分解しましょう。例えば\(\overrightarrow{a}\)について、\(\overrightarrow{b}\)、\(\overrightarrow{c}\)、\(\overrightarrow{d}\)と実数\(s,t,u\)を用いて以下のように分解できます。

\(\overrightarrow{a}=s\overrightarrow{b}+t\overrightarrow{c}+u\overrightarrow{d}\)

\(z\)成分が増えるため、空間ベクトルでは3つのベクトルを利用して表現できることを覚えましょう。

平行条件と空間ベクトル

平行条件についても、平面ベクトルと空間ベクトルでは考え方が同じです。ベクトルが平行の場合、以下の条件が成り立ちます。

\(\overrightarrow{a}=k\overrightarrow{b}\)

実数倍することで同じベクトルになる場合、2つのベクトルは平行です。

なお2つのベクトルが平行の場合、\(x\)成分、\(y\)成分、\(z\)成分の比はそれぞれ同じです。そのため\(\overrightarrow{a}=(a_1,a_2,a_3)\)と\(\overrightarrow{b}=(b_1,b_2,b_3)\)が平行な場合、以下の関係が成り立ちます。

\(a_1:a_2=b_1:b_2\) → \(a_1b_2=a_2b_1\)
\(a_2:a_3=b_2:b_3\) → \(a_2b_3=a_3b_2\)
\(a_3:a_1=b_3:b_1\) → \(a_3b_1=a_1b_3\)

そのため空間ベクトルで平行な場合、以下の関係が成り立ちます。

\(a_1b_2-a_2b_1=0\)
\(a_2b_3-a_3b_2=0\)
\(a_3b_1-a_1b_3=0\)

これが空間ベクトルでの平行条件です。それでは、以下の問題の答えは何でしょうか。

\(\overrightarrow{a}=(2,3,-4)\)のとき、\(\overrightarrow{a}\)と反対向きの単位ベクトルを求めましょう。

立体図形で対角線の長さを得るためには、3つの辺を二乗した後、平方根を利用すればいいです。つまり、三平方の定理を利用することによって対角線の長さを計算できます。

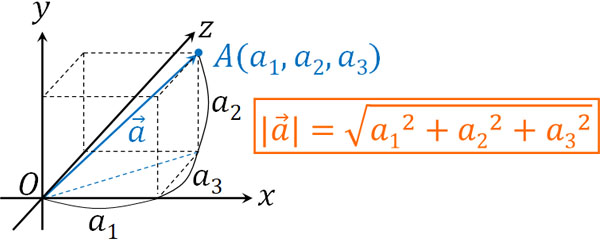
そこで、以下のように\(\overrightarrow{a}\)の長さを計算しましょう。

\(|\overrightarrow{a}|=\sqrt{2^2+3^2+(-4)^2}\)

\(|\overrightarrow{a}|=\sqrt{29}\)

そのため、\(\overrightarrow{a}\)に対して\(\displaystyle\frac{1}{\sqrt{29}}\)倍すれば単位ベクトルになります。なお\(\overrightarrow{a}\)と反対向きにするためには、\(-1\)倍すればいいです。そこで、\(\overrightarrow{a}\)に対して\(-\displaystyle\frac{1}{\sqrt{29}}\)倍しましょう。

その結果、答えは\(-\displaystyle\frac{1}{\sqrt{29}}\overrightarrow{a}=\left(-\displaystyle\frac{2}{\sqrt{29}},-\displaystyle\frac{3}{\sqrt{29}},\displaystyle\frac{4}{\sqrt{29}}\right)\)となります。平行なベクトルを計算したい場合、実数倍することで答えを得ましょう。

2点間の距離とベクトルの大きさの最小値

1つの点について距離を得ることができたら、次は2点間の距離を計算できるようになりましょう。ベクトルの概念は座標とほぼ同じであるため、平面ベクトルの場合と考え方は同じです。例えば\(\overrightarrow{AB}\)の距離を計算するというのは、線分ABの長さを計算するのと意味が同じです。

空間上で2点間の距離を計算するとき、\(x\)成分、\(y\)成分、\(z\)成分でそれぞれの距離を求める必要があります。後から前を引くことにより、それぞれの成分の距離がわかります。例えば\(\overrightarrow{AB}\)の距離を計算したい場合、以下のように計算します。

\(x\)成分：\(b_1-a_1\)
\(y\)成分：\(b_2-a_2\)
\(z\)成分：\(b_3-a_3\)

つまり、以下のようになります。

\(\overrightarrow{AB}=(b_1-a_1,b_2-a_2,b_3-a_3)\)

\(\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}\)であるため、このような計算になります。その後、三平方の定理を利用することによって\(\overrightarrow{AB}\)の長さを計算しましょう。

\(|\overrightarrow{AB}|=\)\(\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}\)

これが、空間ベクトルで2点間の距離を得る公式です。空間図形で距離を得る方法と同じであるため、公式を覚えなくてもベクトルの長さの計算は容易です。それでは、以下の問題を解いてみましょう。

\(\overrightarrow{a}=(0,2,4)\)、\(\overrightarrow{b}=(1,0,1)\)のとき、\(|\overrightarrow{a}-t\overrightarrow{b}|\)が最小になる\(t\)とそのときの大きさ（長さ）を求めましょう。

まず、\(|\overrightarrow{a}-t\overrightarrow{b}|\)を二乗しましょう。\(|\overrightarrow{a}-t\overrightarrow{b}|≧0\)であるため、\(|\overrightarrow{a}-t\overrightarrow{b}|^2\)が最小の場合、\(|\overrightarrow{a}-t\overrightarrow{b}|\)も最小になります。

また、\(\overrightarrow{a}-t\overrightarrow{b}\)を計算すると以下のようになります。

\(\overrightarrow{a}-t\overrightarrow{b}=(-t,2,4-t)\)

そのため、\(\overrightarrow{a}-t\overrightarrow{b}\)の距離の二乗（\(|\overrightarrow{a}-t\overrightarrow{b}|^2\)）は以下のように計算できます。

\(|\overrightarrow{a}-t\overrightarrow{b}|^2\)

\(=(-t)^2+2^2+(4-t)^2\)

\(=t^2+4+(t^2-8t+16)\)

\(=2t^2-8t+20\)

\(=2(t^2-4t)+20\)

\(=2(t-2)^2+12\)

こうして\(t=2\)のとき、\(|\overrightarrow{a}-t\overrightarrow{b}|^2\)の最小値は12となります。そのため\(t=2\)のとき、\(|\overrightarrow{a}-t\overrightarrow{b}|\)の最小値は\(2\sqrt{3}\)です。