小学校で学ぶ内容に約数と倍数があります。小学算数で学ぶとき、約数と倍数の内容は難しくありません。
一方、高校数学でも約数と倍数を学びます。当然ながら、高校数学で学ぶ約数と倍数は内容が難しくなります。約数や倍数には負の数も含まれます。また、新たに覚えなければいけない数式もあります。
なお約数や倍数に理解した後、高校数学では素因数分解を利用して計算することになります。また、約数の個数または総和を数えることができるようにしなければいけません。
高校数学での約数と倍数は内容が複雑です。そこで、どのように問題を解けばいいのか解説していきます。
もくじ
約数と倍数を数式で表す
まず、約数と倍数の初歩から考えていきましょう。例えば、8の約数は何でしょうか。以下のように答えを出すことができます。
- 1, 2, 4, 8
これを数式によって表してみましょう。8の約数というのは以下の数式で表すことができます。
- \(8=b×k\)
\(k\)には何かしらの整数が入ります。また、この数式で\(b\)が約数です。8の約数であれば、以下のようになります。
- \(8=1×8\)
- \(8=2×4\)
- \(8=4×2\)
- \(8=8×1\)
一方、倍数はどのように考えればいいのでしょうか。例えば4の倍数は以下のようになります。
- 4, 8, 12, 16…
そのため、以下の数式によって表すことができます。
- \(a=4×k\)
前述の通り、\(k\)には何かしらの整数が入ります。そこで\(k\)に整数を入れると4の倍数になります。ここまでの解説から、約数と倍数は以下の数式によって表せることがわかります。
- \(a=b×k\)
先ほどの例で提示したことからわかるように、この数式では\(a\)に対する約数が\(b\)です。約数\(b\)と任意の値\(k\)のかけ算によって、\(a\)を得ることができます。
また、\(b\)に対する倍数が\(a\)です。\(b\)に対して任意の値で\(k\)倍することによって、倍数\(a\)を得ることができます。
負の約数、負の倍数も含める
なお、ここまで解説した約数と倍数は実は間違っています。何が間違いなのでしょうか。先ほど、以下が8の約数と解説しました。
- 1, 2, 4, 8
ただ、\(a=b×k\)で表される\(b\)や\(k\)は整数です。つまり約数では、負の約数も含むのです。そのため、\(8=b×k\)では以下のように考えます。
- \(8=1×8\)
- \(8=2×4\)
- \(8=4×2\)
- \(8=8×1\)
- \(8=-1×-8\)
- \(8=-2×-4\)
- \(8=-4×-2\)
- \(8=-8×-1\)
このように考えると、8の約数は以下になるとわかります。
- 1, 2, 4, 8, -1, -2, -4, -8
同じように、負の倍数も存在します。4の倍数は\(a=4×k\)で表されます。\(k\)には、正の値だけでなく負の値も含まれます。そのため、4の倍数は以下のようになります。
- …-16, -12, -8, -4, 0, 4, 8, 12, 16…
重要なのは、負の数も約数と倍数に含まれることです。
高校数学での約数・倍数の練習問題
それでは、ここまで解説した内容をもとに練習問題を解いてみましょう。以下の答えは何でしょうか。
- \(a\)が0ではないとき、\(\displaystyle\frac{a}{4}\)と\(\displaystyle\frac{32}{a}\)の両方とも整数となる\(a\)を求めましょう。
\(\displaystyle\frac{a}{4}\)が整数になるためには、\(a\)が4の倍数でなければいけません。4の倍数というのは、\(a=4k\)で表すことができます。
次に、\(\displaystyle\frac{32}{a}\)が整数になるにはどうすればいいのでしょうか。\(a=4k\)であるため代入しましょう。以下のようになります。
\(\displaystyle\frac{32}{a}\)
\(=\displaystyle\frac{32}{4k}\)
\(=\displaystyle\frac{8}{k}\)
つまり\(k\)に何かしらの値を代入するとき、\(\displaystyle\frac{8}{k}\)が整数になればいいです。これはつまり、8の約数を答えればいいとわかります。8の約数は以下になります。
- 1, 2, 4, 8, -1, -2, -4, -8
そこで\(a=4k\)に代入すると、以下が答えになります。
- 4, 8, 16, 32, -4, -8, -16, -32
倍数の判定法を理解する
なお倍数を学ぶとき、倍数の判定法を習うことがあります。小さい数であれば、約数や倍数の判断が簡単です。一方、大きい数字だと判断しにくいです。例えば、1941は3の倍数でしょうか。
倍数の判定法を知っていれば、約数や倍数を見つけるのが容易になります。そこで、どのようにして倍数を判定すればいいのか理解しましょう。なお、ここでは自然数(正の整数)に限って話を進めていきます。
倍数の判定法で重要なポイントは以下になります。
- 2の倍数:一の位が偶数
- 3の倍数:それぞれの位の和が3の倍数
- 4の倍数:下二桁が4の倍数
- 5の倍数:一の位が0または5
- 8の倍数:下三桁が8の倍数
- 9の倍数:それぞれの位の和が9の倍数
倍数の判定法では、これらを覚えておけば問題ありません。
倍数判定法の証明(一部)
なお、2の倍数の判定法は誰でもわかります。偶数であれば2の倍数です。一方、3の倍数はどのように判断すればいいのでしょうか。すべてを証明すると非常に長くなるため、一部だけ証明します。
・3の倍数を見分ける方法の証明
まず数字というのは、以下のように表すことができます。
- \(a+10b\)\(+100c+1000d+…\)
例えば、736は以下のように表せます。
- \(6+10×3\)\(+100×7\)
そこで、以下のように式を変形してみましょう。
\(a+10b\)\(+100c+1000d+…\)
\(a\)\(+(b+9b)\)\(+(c+99c)\)\(+(d+999d)\)\(+…\)
\((a+b+c+d+…)\)\(+3(3b+33c+333d\)\(+…)\)
\(3(3b+33c+333d\)\(+…)\)の部分は3の倍数です。そのため、\((a+b+c+d+…)\)が3の倍数の場合、数字は3の倍数になります。これが、それぞれの位の和が3の倍数だと、数字も3の倍数と判断できる理由です。
・4の倍数を見分ける方法の証明
次に、4の倍数を考えてみましょう。4の倍数では、\(100c\)や\(1000d\)は必ず4の倍数になります。
\(100c=4×25c\)
\(1000d=4×250d\)
そこで、数字を以下のように変えましょう。
- \((a+10b)\)\(+4(25c+250d+…)\)
そうすると、\((a+10b)\)が4の倍数であれば、数字は4の倍数であると判断できます。このように、それぞれの倍数判定法を証明していくと、先ほど解説した倍数判定法を導けます。
倍数判定法を利用して問題を解く
それでは、以下の問題の答えは何でしょうか。
- \(84724☐2\)が4の倍数のとき、\(☐\)に当てはまる自然数をすべて答えましょう。
倍数判定法を利用すると、下2ケタが4の倍数のとき、数字は4の倍数になります。そのため、\(☐2\)が4の倍数になるケースを考えればいいです。そうすると、以下のケースで4の倍数になるとわかります。
- 12
- 32
- 52
- 72
- 92
そのため、\(☐\)に当てはまる数字は1, 3, 5, 7, 9とわかります。
素数と素因数分解:整数\(k\)を用いて計算する
なお約数を学んだあと、私たちは素数を習いました。1とそれ自身の数以外に正の約数をもたない場合、素数といいます。例えば7を割れる数は1と7だけなので、7は素数です。
このとき素数を利用し、割り算をすることを素因数分解といいます。平方根を利用するとき、素因数分解が重要になります。数式を用いて素因数分解をするとき、ここまで解説した\(a=bk\)(\(k\)は任意の整数)を利用することによって問題を解くことができます。
例題として、以下の問題を解いてみましょう。
- \(\displaystyle\frac{n}{4}\)と\(\displaystyle\frac{n^2}{32}\)の両方が自然数となるとき、最小となる\(n\)の値を求めましょう。
まず、\(\displaystyle\frac{n}{4}=k\)としましょう。そうすると、以下のようになります。
\(n=4k\)
こうして、\(n\)は4の倍数であるとわかります。次に、\(n=4k\)を代入しましょう。
\(\displaystyle\frac{n^2}{32}\)
\(=\displaystyle\frac{(4k)^2}{32}\)
\(=\displaystyle\frac{16k^2}{32}\)
\(=\displaystyle\frac{k^2}{2}\)
こうして\(k=2\)のとき、\(\displaystyle\frac{n^2}{32}\)は正の整数になります。そのため、\(n=4×2=8\)が答えであるとわかります。
約数の個数を求める公式
素因数分解を理解したら、約数の個数と総和を求める公式を覚えましょう。まず、約数の個数から解説していきます。
数字\(N\)を素因数分解することによって、以下の結果を得たとします。
- \(N=p^a×q^b×r^c×…\)
この場合、約数の個数は以下の公式によって得ることができます。
- \((a+1)(b+1)(c+1)…\)
それでは、なぜこの公式によって約数の個数を得ることができるのでしょうか。公式を覚えても高確率で忘れるため、理由を理解することによって公式を作れるようになりましょう。
例えば300を素因数分解すると以下のようになります。
\(300=2^2×3×5^2\)
この場合、以下のように何通りの方法があるのか計算することができます。
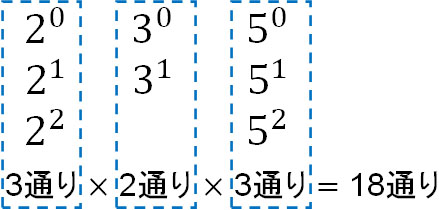
このように、順列の計算によって約数の個数を計算できます。そのため、約数の個数を計算する公式を覚える必要はありません。
約数の総和を計算する方法と考え方
それでは、次に約数の総和を求めましょう。\(N=p^a×q^b×r^c\)のとき、以下の公式によって、約数をすべて足すときの値を得ることができます。
- \((1+p+p^2…+p^a)\)\((1+q+q^2…+q^b)\)\((1+r+r^2…+r^b)\)
例えば\(300=2^2×3×5^2\)について、以下のように約数の総和を求めることができます。
\((1+2+2^2)\)\((1+3)\)\((1+5+5^2)\)
\(=7×4×31\)
\(=868\)
それでは、なぜこの公式によって約数の総和を求めることができるのでしょうか。例として、20の総和を考えてみましょう。\(20=2^2×5\)であるため、以下の約数が存在します。
- \(1×1\)
- \(1×5^1\)
- \(2^1×1\)
- \(2^1×5^1\)
- \(2^2×1\)
- \(2^2×5^1\)
これらをすべて足すため、以下の式を作りましょう。
\(1×1\)\(+1×5^1\)\(+2^1×1\)\(+2^1×5^1\)\(+2^2×1\)\(+2^2×5^1\)
\(=(1+5^1)\)\(+2^1(1+5^1)\)\(+2^2(1+5^1)\)
\(=(1+2^1+2^2)(1+5^1)\)
このように、先ほどの公式を利用して計算した方法と同じやり方を導き出すことができます。約数の個数とは異なり、約数の総和を求める場合、公式を覚えておく必要があります。ただ、なぜ公式が成り立つのか理解することは重要です。
約数の個数や総和を求める公式を利用して問題を解く
それでは、以下の問題を解いてみましょう。
- \(675^a\)について、約数の個数が35となる自然数\(a\)を求めましょう。
\(675^a\)は以下のように変形することができます。
\(675^a=(3^3×5^2)^a\)
\(=3^{3a}×5^{2a}\)
約数の個数は35であるため、以下の式を作ることができます。
\((3a+1)(2a+1)=35\)
この式の答えを出しましょう。
\((3a+1)(2a+1)=35\)
\(6a^2+5a+1=35\)
\(6a^2+5a-34=0\)
\((6a+17)(a-2)=0\)
\(a\)は自然数なので、答えは\(a=2\)です。こうして、公式を利用することによって答えを出すことができました。
高校数学で約数と倍数の計算を行う
小学校で学ぶ約数や倍数とは異なり、高校数学で学ぶ約数と倍数は難易度が一気に上がります。そのため、問題を解くのが難しくなります。そこで、約数と倍数をどのように数式で表すのか学びましょう。\(a=b×k\)によって約数と倍数を表すことができるため、この数式を利用することによって問題を解くのです。
また約数と倍数の問題では、倍数判定法を利用しなければいけないケースがあります。この場合、倍数判定法を覚えていなければ問題を解けません。
他には、約数の個数や総和を問われる問題がひんぱんに出されます。公式を利用することによって、約数の合計個数や総和を計算できるようにしましょう。
約数や倍数を高校で学ぶとき、新たな数式や公式を覚えなければいけません。そこで、これらの公式を利用して問題を解きましょう。